TILT ANGLE 8, deg

Fig. 6-8—Penetration of Zn parallel and perpendicular to the [011] rotation axis of Al
bicrystals. [I. Herbeuval, M. Biscondi, C. Goux, Mem. Sci. Rev. Met., 70 (1973) 39.]

Clearly there is a variation with angle and a minimum at the coherent twin orientation (/ = 3). The lack of symmetry reflects scatter in the data and scatter in the misorientation of the bicrystals used.

Temperature Dependence. Experimental results clearly indicate that the activation energy for grain boundary diffusion is less than that for lattice diffusion, while D_o is about the same for the two. This is born out by the data in Table 6-1. The samples used to get this data were polycrystalline and the observed penetration will be weighted to­ward high angle grain boundaries with higher values of D_b8.

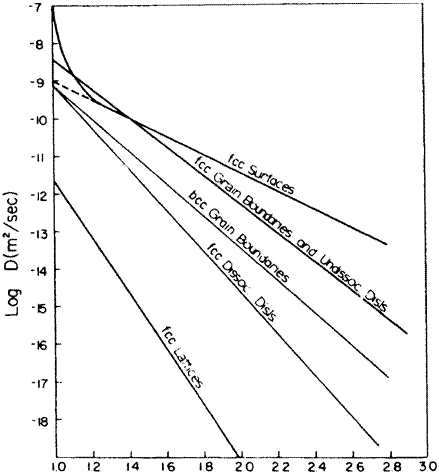
If one compares DO for different types of grain boundaries, the re­sults can be rationalized in terms of the atomic packing in the given boundary compared to the packing (density) in a perfect lattice. If there is more open space a grain boundary, some of the atoms will be able to jump with a lower activation energy than if the atoms are more tightly packed. A lower Q will translate into a higher value of D. Such behavior is shown in Fig. 6-9 which represents the spectrum of data for D in: boundaries made of undissociated dislocations or high angle boundaries (Q_b/Q, = 0.4-0.5), dissociated dislocations and twist boundaries (Qb/Qi = 0.6-0.8), and lattice diffusion. For the same misorientation between two grains, diffusion down a twist boundary is 10 to 100 times slower than down the tilt boundary. Examination of a tilt boundary shows that it has clear regions of low density while a twist boundary involving screw dislocations has little dilatation and primary shear strains. (The surface diffusion curve is discussed below.)

T_m~T(K)

Fig. 6-9—Diffusivity vs. reduced reciprocal temperature for various diffusion paths in metals. [N. Gjostein, in Diffusion, ASM, Metals Park, OH, (1973) p. 241-74.]

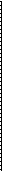Mechanism. Calculations using molecular dynamics models have been made on models of dislocations, and a few on segments of grain boundaries. Fig. 6-10 shows several consecutive planes normal to the plane of a 6 = 36.9° [1001 tilt boundary (I = 5) in a bcc lattice. This boundary is 'high angle', but also has a relatively small repeat distance along the boundary in the planes shown. Thus the size of the model needed for calculations is reasonable. The results for diffusion in such a grain boundary indicate that both the motion energy and the for­mation energy of a vacancy are less than in the lattice, with the re­duction in the energy of motion being about twice the reduction in the formation energy.^1° Other conclusions are:

• Vacancy jumps along the grain boundary core, of the sort B —p D —> B or B ---> C —> B are the most frequent.

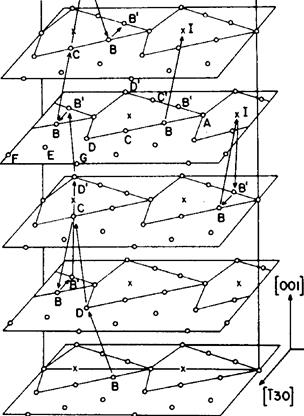
Fig. 6-10--Structure of IR = 5 [110] tilt boundary in bcc lattice showing repeated triangular units, and jump sequences along the core designated by arrows between at­oms with letters beside them. (after R. W. Balluffi)

· Movement in the boundary normal to the core is much slower than along the core, that is, anisotropy in DO persists at the high angles.

n Interstitials can form relatively easily, but move slowly.

The interatomic potentials used for such calculations do not give accurate values of the energies involved, but authors working with models of a variety of metals, for both dislocations and grain bound­aries, all agree that diffusion is primarily by vacancy motion. This conclusion is further strengthened by the observation that the activation volume for diffusion in high-angle grain boundaries in silver is larger for boundary diffusion than for lattice diffusion, namely Vb is 1.1 f2 while V_i = 0.9 fl." This large Vb also lends credence to the basic idea that vacancies exist in the boundary which are very similar to those existing in the lattice.

Alloying Effects. Alloying elements often segregate at grain bound­aries or dislocations. This is especially true for elements whose sol­ubility is low. This can have two distinctly different effects:

^HG. Martin, D. A. Blackburn, Y. Adda, Phys. Status Solidi, 23 (1967) 223.

· The binding to the high diffusivity path raises the mean diffusion coefficient of the impurity because it spends a larger fraction of the time where it diffuses faster.

· The solute can change the boundary structure, for example fill in open spaces and make it harder for atoms to move along the bound­ary or dislocation.

The first effect of segregation can most easily be treated by consid­ering the boundary condition between the grain boundary and the lat­tice. Rather than the concentration being equal in the two regions, Eq. (6-5) becomes

c_b(5/2) = Kc₁(3/2) (6-11)

Subsequent equations are unchanged except that DO is replaced in all equations by KD_b8.

The second effect cannot be quantified as simply, nor is there any widely accepted theory of solute diffusion or the effect of solutes on solvent diffusion, as there is for lattice diffusion.

6.3 DISLOCATION & GRAIN SIZE EFFECTS

The treatment above dealt with the measurement of Db and D_i, in bicrystals. Consider now the effect of randomly oriented dislocations, or a fine grain size. These are of interest in studying the kinetics of diffusion limited processes at or below half the melting temperature, and are central in determining the rate of diffusion in fine grained thin films.

There is great similarity between the results for diffusion enhanced by a three dimensional array of dislocations^u and that arising from a 3-D array of grain boundaries.¹³ We will describe the results for dis­locations, and then compare the results with those for boundaries. Con­sider the regular array of dislocation pipes of radius 'a' and separation 2Z as shown schematically in Fig. 6-11. They are normal to the free surface, which has solute on it. The section can show three different types of solute distributions depending on the ratio of the mean dif­fusion distance in the lattice \//s_it^- to the separation Z, and remem­bering that D_i, is always much larger than D_I.

· 1/D₁t Z, an atom interacts with several dislocations in diffusing
this far through the lattice. The dislocations increase the effective

'²A. D. LeClaire, A. Rabinovitch, in Diffusion in Crystalline Solids, ed. G. Murch, A. Nowick, Academic Press (1984) pp. 259-319.

'D. Gupta, D. R. Campbell, P. S. Ho, in Thin Films—Interdiffusion and Reactions, eds. Poate, Tu & Mayer, J. Wiley & Sons, (1978) pp. 161-242.

Fig. 6-11—Schematic representation of the various concentration profiles that can de-
velop with different ratios of V(D_it)/Z. The solute source is at the top of each figure.

diffusivity D_eff for the solid, so that the penetration depth is greater than it would be without dislocations. The advancing isoconcentra­tion lines are relatively flat near the dislocations. This will be re­ ferred to as 'A-kinetics.'

· VD _it C Z, but VD_it a. The solute field around each dislocation develops independently of its neighbors, and the situation is similar to the case of grain boundary diffusion in bicrystals analyzed above. B-kinetics.

· VD₁t < a, Diffusion occurs only in the dislocation pipes with no loss to the surrounding lattice. This is rare in bulk samples, but in a thin film at T =0.5 T„„ 13₁,/D₁ can equal 10⁸ (see estimate for Ag above) and diffusion through a one micron thick film can occur with­out any solute being lost to the lattice. C-kinetics.

Дата добавления: 2015-10-29