High diffusivity paths

In the preceding chapters the only defects which aided diffusion through the crystal were vacancies and interstitials. Dislocations, free surfaces, and grain boundaries entered only to help attain the equilib­rium defect concentration. However, it is now well established that the mean jump frequency of atoms at dislocations, boundaries, or surfaces is much higher than that of the same atom in the lattice. The diffusivity is therefore higher in these regions. This higher diffusivity is of interest for several reasons. First, there is the question of what error these paths introduce in the measurement of the lattice diffusion coefficient. Also, with properly designed experiments it is possible to determine the dif­fusion coefficients in each of these high diffusivity regions, allowing one to learn more about the structure of these paths and about how the atoms move in them. Finally, there are a group of kinetic processes which are limited by such diffusion, for example diffusional creep, structural changes in thin films, or the stability of fine catalysts.

As an example of the phenomena we are talking about, the contri­bution of diffusion along grain boundaries can be seen in Fig. 6-1. Here the apparent self-diffusion coefficient in silver is shown for sin­gle-crystal and polycrystal samples. This apparent diffusion coefficient is just that value of D obtained by plating radioactive silver on the surface of the specimen, diffusing it, and then determining D from a plot of /n(activity) vs. penetration distance squared. At high temper­atures, the same value of D is obtained from both types of samples. However, below 700° C the values of D obtained using a polycrystal consistently lie above the values obtained with a single crystal. The high-diffusivity paths' in this case are grain boundaries. Below about

^IZener coined the phrase "short-circuiting paths" to describe this type of effect. For one accustomed to thinking in terms of the electrical analogue of diffusion, it is ap­parent that a high-diffusivity path corresponds to one of high conductivity, and this will tend to relieve the potential gradient or act like a short circuit. However, this analogy is not immediately apparent to many, and the phrase "high-diffusivity path" is used here.

Temperature,°C

900 800 700 600 500 450 400 350

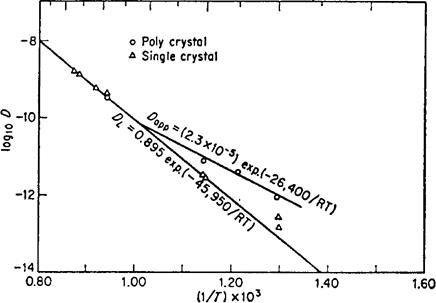
Fig. 6-1—Values of DT for silver in silver single-crystals and polycrystalline samples. [D. Turnbull, in Atom Movements, ASM, Cleveland, (1951) p.129.]

600^° C (0.7T_m) the contribution of the grain boundary region becomes dominant.

An estimate of the increase in the jump frequency in the neighbor­hood of a grain boundary can be obtained as follows. In pure silver the smallest grain diameter which can be retained at high temperatures will be about 1 mm. If this is true and the high-diffusivity region around a grain boundary is taken to be 3 x 10^-8 cm wide, about one atom in 10⁶ will be in the grain boundary. At 650⁰ C these few grain bound­aries double the measured diffusion coefficient. If one-millionth of the atoms make a contribution to the jump frequency which is comparable to that of all the rest of the atoms, then each of these must be jumping roughly one million times as often as the regular lattice atoms. At lower temperatures the difference between the jump frequency in the grain boundaries and that in the lattice is even larger. Since the grain boundary atoms represent such a small part of the specimen, it also follows that the mean jump frequency in this region can be a few or­ders of magnitude larger than it is in the lattice, for example 10³ times, and still the boundary regions will make no significant contribution to the total flux.

The first problem to be dealt with is how to measure the diffusion coefficient in these high-diffusivity paths. These paths cannot exist ex­cept as regions surrounded by otherwise perfect crystals, so some means must be found of treating measurements made on samples in which the surface atoms represent a very small fraction of the atoms in the

sample. Two types of such experiments are discussed. The first uses a concentration gradient as a driving force and the accumulation of solute to measure the total amount of material transported. The second uses surface tension as a driving force and obtains the total flux from the change in the shape of the sample.

Дата добавления: 2015-10-29