THERMO-TRANSPORT—Interstitial Alloys

The fact that a temperature gradient can lead to the unmixing of an initially homogeneous alloy indicates a biasing of the jumps either up, or down, the temperature gradient. For a situation in which only one component is diffusing, e.g. an interstitial alloy, the flux equation can be written

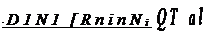
D_iIRT is the mobility of component 1, (0/T)dT/dx is the effective force exerted by the temperature gradient, and RT(a/nN_i/ax)_T is the chemical potential gradient at constant temperature. 0 is the experi­mentally determined parameter which describes the sign and magni­tude of the thermo-transport effect. It is called the heat of transport of component 1; the rest of our discussion of thermo-transport will be devoted to its interpretation and measurement. Note that D₁ is the iso­thermal diffusion coefficient. The temperature gradient changes neither the jump mechanism, nor the mean jump frequency at any given tem­perature; it does bias the direction of jumps.

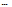
•e

1.60
1.40

N h
N_e

1.20

1.02 1.04 1.06

10³/T, °K

Fig. 7-5 — Plot of carbon content (logarithmic scale) vs. 1 /T for a-Fe annealed in a temperature gradient until steady state is attained. [P. Shewmon Acta Met., 8 (1960) 606.]

Q* can be measure either by letting the flux go to zero in a tem­perature gradient and measuring the concentration gradient at J = 0, or by measuring the flux through an open system under a known tem­perature gradient. Figure 7-5 shows the concentration gradient ob­tained when an initially single-phase iron-carbon alloy (0.01 %C) was held in a temperature gradient until a steady state was established. The flux was then equal to zero and Eq. (7-7) gives

dinN ₁ --QT dT

= -........■ ■

dx RT² dx

During the anneal the carbon concentration became higher at the hot
end, indicating that Q* is negative.⁶ The line drawn through the points
gives a value of Q),'(a) = —96 kJ/mol, and suggests it is independent

⁶The off-scale points on the left side of Fig. 7-5 result from the precipitation of iron carbide in this region and in no way affects the determination of dlnlVidT in the single phase portion of the specimen. The redistribution of a second phase during annealing in a temperature gradient is discussed below.

of temperature. Experiments made on the same low-carbon alloy in y-iron temperature range gave Q.`(y) —8. Note that one does not have to know the diffusion coefficient to obtain Q* in this way.

Q* can also be obtained from measurements of the flux. Measure­ment of the flux of atoms in a pure metal in a temperature gradient, relative to the lattice, has been made by following the movement of markers, as was described above for electrotransport (see Fig. 7-3).

Examples of data for Q* for interstitial alloys are given in Table 7­2. Much of the data is for the rapidly diffusing hydrogen, H, and its isotope of mass 2, deuterium. For hydrogen the magnitude of Q* clearly rises with temperature, and rises in going from hydrogen (H) to deu­terium (D). Note also that the sign of Q* is often opposite to that of z*, the effective charge on the ion in electrotransport.

Theory of Q*. The name 'heat of transport' for Q* and its use in Eq. (7-7) stems from the equations of irreversible thermodynamics. For a system in which there is both a flux of matter and of heat, the equations for the heat flux.1,, and the solute flux J₁ can be written

J 1 = ^—L11(a/¹11 aX)T (Li_qin(aT aX)N1 (7-9)

J_q = ^—4011 aX)T (L_qq/T)(aT aX)N1 (7-10)

where the gradients have been taken parallel to the x-axis. These equa­tions express the flux as the sum of a force due to the chemical po­tential gradient at constant temperature and a temperature gradient at constant composition. The flux equation for J₁ can be rewritten

J1 = ^—LiiRagiax)T (Li_qflatiT)(aTlax)]
Comparing this with Eq. (7-7), if L_I/ is set equal to D_iN_i/RT then Q*,'

Table 7-2. Q* for Interstitial Alloys

Q*

Solvent Solute (kJ) Ref.

fcc

H —23.5 1 Ni H

D —22 1 Ni D

C —59 2 Ni C

H 7.5 3 Co C

D 20 3 Pd H

C —20.5 2 Pd C

'0. Gonzales, 'J. Shaw, W. ^3D. Peterson, ^41. Okafor, 0.

R.Oriani, TA1ME, 223 (1965) 187. Oates, Met. Trans., 2A (1971) 2127. M. Smith, Met. Trans., 13A (1982) 821. N. Carlson, D. Martin, Met. Trans., 13A (1982) 1713.

Thermo- and Electro-Transport in Solids 233

L_ig/L_{i 1}. But if (aT/ax) 0, the ratio of Eqs. (7-10) and (7-9) gives

(Jq/J1)T LaLli = Lqi/Lii = (7-11)

where the Onsager reciprocal relation, Li_lq = L_q,, holds since we have selected the forces in Eq. (7-9) and (7-10) appropriately.' Qf is thus the heat flux per unit flux of component 1 in the absence of a tem­perature gradient. If > 0, a heat flux parallel to./₁ will be generated by a solute flux; that is, to keep the region gaining solute atoms iso­thermal, heat must be removed from it. If Q^*₁ < 0, .1_q and J₁ are in opposite directions, and the region gaining solute atoms must receive heat to keep it isothermal.

Heat in a metal is carried by free electrons and elastic waves in the lattice (called 'phonons'). In the presence of a temperature gradient the jumps of the moving atoms are biased by the interaction of the atom with electrons, phonons, and/or gradient related assymetries in the activation process. The interaction is difficult to treat with preci­sion, but qualitatively there are two contributions. One force stems from the interaction with flowing electrons, and the other from gra­dient related assymetries in the activation process.

In a simple metal in a temperature gradient the kinetic energy of the free electrons on the hot side of the sample are raised by adsorbing heat from the heat source, while on the cold side the kinetic energy of the free electrons is lowered by giving up heat to the heat sink. The heat is carried in the solid by the flow of more energetic electrons from the hot to the cold side, while less energetic electrons flow in the re­verse direction to maintain charge neutrality. This gradient induced flow of higher energy electrons biases the jumps of the atoms in the same direction, that is it induces an electron 'breeze' in the same way that a current flow does in electro-transport. Qualitatively this predicts that if z* is negative then Q* will be positive, since the flow of neg­atively charged electrons down the temperature gradient biases the mo­tion of atoms in the same direction as that of the electrons. Such a correlation between the sign of —z* and Q* is common, but not universal.

A kinetic argument due to Wirtz treats the biasing of jumps without any reference to the flux of energy through the solid. In an isothermal system the probability that a given solute atom will be in the high-energy configuration required for a jump is related to the temperature of the region through the factor exp(-1-1,_i/RT). In the presence of a

⁷A useful, simple introduction to these relations is given by K. G. Denbigh, The Thermodynamics of the Steady State, Methuen & Co., (1951). The forces have been chosen so that the product of the flux J, and the force X, has the units (tempera­ture)(entropy)/(time)(volume).

temperature gradient, the average temperatures of the original, inter­mediate, and final planes of the jumping solute will be different. As a result, the frequency with which the required high-energy configu­ration is established for a jump to the higher temperature side may differ infinitesimally from that for a jump to the lower temperature side. To obtain an equation for these two jump frequencies, assume that H_m consists of three parts:

1. That given to the atoms on the original plane of the solute (H₀),

2. That given to the atoms in the intermediate plane of the jump (H_i),

3. That required to prepare the final plane for the jumping atom (H_f). The jump frequency for the atoms moving up the temperature gradient will then be proportional to the product

)

(^-110) (_______ 11, — Hf

Exp

RT exp R(T + 4T/2) ^exp) (R(T + AT)

where the average temperature difference between the original and the final plane of the jumping solute is 4T. The jump frequency for atoms jumping in the reverse direction between the same two planes will be proportional to:

exp(— —Hf)(—H_i (—H_o
RT)
exp R(T + AT/2) exp ) R(T + AT)
The middle term in both of these equation is the same so the ratio of

---

Дата добавления: 2015-10-29