The jump frequencies is

(--H_c, + H_f) (—H_f + H„

Exp exp

RT R(T + AT)

If n_h and n, are the number of atoms per unit area on the hotter and colder planes, respectively, the condition for zero flux between the planes is

n_h (—H_o + Il_f) (—H_f+ H_o)

— = exp exp

n, RT R(T + AT))

= exp(- --Hf)AT

(7-12)

—(H,)

RT² (1 + AT a)

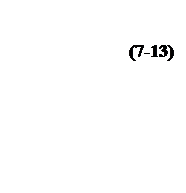But (n_h — 10/ n,, and AT /T are both much less than one, so this equa­tion can be put in differential form as

d ln(n) —(H, — H_f) dT

dx RT² dx

Comparing this with Eq. (7-8), the equation for Q1 for this model is

Q* = H_o — H_f (7-14)

Since H_o, H_i, and H_f were defined such that H„, = H p + H_i + H_f, Eq.
(7-14) requires that Qs*1 H,, but allows any value of Q* in this range.

This model indicates that Q* is influenced by the spatial distribution of the activation energy required for a jump. In Chap. 2 the atomic mechanisms and atomic rearrangements required for an atomic jump were discussed. The most common situation was one in which the diffusing atom had to pass through a constriction on its way to a rel­atively open, new site. If the primary barrier to diffusion were the movement of constricting atoms out of the way so that the diffusing atom could pass, then most of H_m would be located in the intermediate plan, H„, would then be about equal to H, and Eq. (7-14) indicates that Q* would be almost zero. On the other hand, if the main part of 11,,, were required to make the diffusing atom execute violent enough oscillations to move it to the saddle point (the constriction always being relatively open), the result would be H,,, = H,, and Q* = H_o. In this latter case the solute would tend to concentrate at the cold end. This result can be seen by noting that if H„, = H,, the jump frequency of the solute atoms on the hotter of two adjacent planes will always be greater than that of the solute on the colder plane. Thus if the number of atoms jumping from the cold plane to the hot plane per unit time is to equal the number making the reverse jump, there must be more solute atoms on the colder plane.

A system to which the Wirtz model seems to apply is carbon in iron. The data in Table 7-2 indicate that Q* in bcc iron is negative and roughly equal in magnitude to the H„„ while in fcc iron Q* is close to zero even though H„, is almost twice that in bcc iron. In an fcc lattice an interstitial atom must pass through a pronounced constriction in a jump from one interstitial site to another (see Fig. 2-3). Thus it is plausible to say that H, would be an appreciable part of H„,, and Q* would be expected to be small, as it is. The large negative value of V_ci` in the bcc a-iron may at first seem anomalous since its interpre­tation using Eq. (7-14) requires that most of H„, goes into preparing the plane of the final site for the jump. However, examination of the bcc lattice, e.g. Fig. 7-6, shows that the moving atom must pass through no constriction midway along its jump. The major barrier to be over­come in the movement of an interstitial atom from one site to an ad­joining one appears to be the moving apart of two iron atoms in the final plane so that the carbon atom can jump from its initial position into a position between them.

Discussions of the theory of Q* usually involve some combination

Fig. 7-6—Model of interstitial atom moving in bcc lattice. The dashed circles rep­resent the new positions of matrix atoms after the interstitial atom makes the jump shown by the arrow.

of these two effects, that is the 'electron breeze', and the Wirtz model.
The theory is qualitatively satisfactory, but quantitatively poor, since
there is no way to determine the exact contribution of each effect to

Q*

Precipitation and Phase Redistribution. Interstitials diffuse rap­idly and also often form precipitates with a low solubility. This can cause the precipitates in a two phase alloy to redistribute in a temper­ature gradient. Or, it can lead to the formation of a precipitate at one end of a sample in an alloy which was a solid solution when the alloy was placed in a temperature gradient. As an example of the latter case, consider the diffusion of hydrogen in zirconium. Q* is positive for this system (6 kcal/mol), thus thermo-transport pushes the hydrogen to­ward the cold end of a sample in a temperature gradient. The solubility of zirconium hydride drops as the temperature decreases, so if the con­centration of hydrogen in Zr was initially near the solubility limit at the lower temperature, the flux due to thermo-transport will raise the concentration at the cold end above the solubility limit and precipi­tation at the cold end will result. Fig. 7-7 shows initial and final dis­tribution of hydrogen in a dilute zirconium alloy after annealing in a

TEPtPERATURE (C)

150 300 450

POSITION

Fig. 7-7—Hydrogen distribution in Zr after annealing an initially single phase alloy in a temperature gradient. [After A. Sawatzky, inl. Nucl. Mall., 2 (1960) 450.

temperature gradient, as well as the solubility of the hydride as a func­tion of temperature. The initial H concentration was above the solu­bility of H at the cold end of the sample, so a precipitate forms at the cold end, as one would expect. However, the amount of hydrogen found at the cold end after the anneal far exceeds the initial content. This is because most of the hydrogen initially in the higher temperature region has diffused down to form a precipitate at the cold end. In the high temperature region where there is no precipitate, the concentration of hydrogen in solution drops steadily from the solubility limit. This is consistent with a positive Q*. The H concentration increases rapidly where the solubility of the hydride is exceeded, since any hydrogen swept into this region by the temperature gradient forms a precipitate.

---

Дата добавления: 2015-10-29