Сформулируйте и докажите необходимое условие сходимости числового ряда. Приведите пример расходящегося ряда, для которого это условие выполнено.

Ответ: Необходимый признак сходимости: Пусть числовой ряд a₁+a₂+…+a_n+… сходится, а S – его сумма. Тогда при неограниченном возрастании числа n членов ряда его общий член a_n стремится к нулю

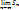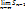Док-во: Так как S_n-S_n-1=a_n и a_nà0, то =S и =S

Поэтому =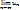

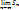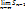= - =S-S=0

Пример:

ln(1+ )+ln(1+ )+…+ln(1+ )+…

ряд расходится, хотя общий член стремится к нулю при nà∞

17. Докажите, что если ряд 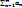, a­_n≥0, а ряд 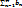расходится, то ряд 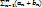расходится

Ответ:

18. Докажите, что для сходимости ряда 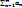, a_n≥0 необходимо и достаточно, чтобы последовательность его частичных сумм была ограничена

Ответ: Для того, чтобы ряд 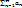с неотрицательными членами сходился, необходимо и достаточно, чтобы последовательность частичных сумм этого ряда была ограничена.

Док-во: Необходимость: Пусть ряд 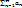сходится. Это значит, что последовательность его частичных сумм имеет предел. Всякая сходящаяся последовательность является ограниченной

Достаточность: Пусть последовательность частичных сумм ряда 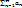ограничена. Т.к. ряд 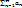с неотрицательными членами, то его частичные суммы образуют не убывающую последовательность: 0≤S₁≤S₂≤…≤S_n-1≤S_n≤…

Монотонная ограниченная последовательность сходится, т.е. сходится ряд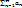

Сформулируйте и докажите признак Даламбера для числовых рядов с положительными членами

Ответ: Признак Даламбера: Если для ряда a₁+a₂+…+a_n+… с положительными членами существует предел L= 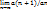, то при 0<L<1 ряд сходится, а при L>1 – расходится. Замечание: при L=1 признак ответа не дает.

Док-во: Пусть L<1. Тогда для ε= 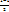>0 существует n₀, такое что 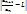< ε= =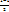

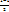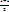–L< ; < = q

Тогда q<1, т.к. L<1

Имеем:

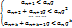
В силу первого признака сравнения рядов из сходимости ряда a_n+a_nq+…+a_nq^k+… при 0<q<1 следует сходимость ряда a_n+a_n+1+…+a_n+k+…

Док-во закончено. Для случая L>1 док-во аналогично, но получается сравнением с суммой геом. прогрессии, где q>1

Сформулируйте признак Даламбера в предельной форме. Приведите пример сходящегося ряда с положительными членами, к которому этот признак неприменим.

Ответ: Если существует p= 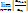, то рассматриваемый ряд абсолютно сходится если p<1, a если p>1 – расходится.

Пример ряда: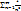

Дата добавления: 2015-10-23