Не имеет предела в точке (0,0)

Дайте определение предела функции двух переменных в точке.

Ответ: Конечное число A называется пределом функции f(x,y) при xàx₀ и yày₀, если для любого положительного числа ε можно найти такое положительное число δ, что неравенство |f(x,y)-A|<ε выполняется для всех точек М(х,у) из области Z, отличных от M₀(x₀y₀), координаты которых удовлетворяют неравенствам: |x-x₀|< δ, |y-y₀|< δ

7. Докажите, что функция f(x,y)=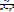

не имеет предела в точке (0,0)

Ответ: Если в точке (0,0) существует предел, то он единственен.

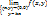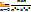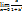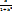= = = = = A(k)

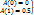=> различны пределы => пределы различны

8. Как связаны производная по направлению и градиент дифференцируемой функции f(x,y)? Чему равна производная по направлению, перпендикулярному градиенту?

Ответ: Производной функции f(x,y) в точке (x0,y0) по направлению называется предел |_M=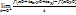

Эта же производная по направлению =(cosα,cosβ) может быть вычислена по формуле: |_M = |_M cosα + 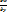|_M cosβ.

Под градиентом функции f(x,y) понимается вектор-функция, проекциями которой являются ее соответствующие частные производные, т.е.

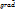f(M) = (, ).

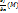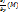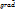На основании определения можно переписать формулу производной по направлению как скалярное произведение (M) =( f(M), )

9. Дайте определение градиента функции f(x,y) в точке (x₀,y₀). Докажите, что в направлении градиента происходит наиболее быстрый рост функции. Чему равна скорость этого роста?

Ответ: Под градиентом функции f(x,y) понимается вектор-функция, проекциями которой являются ее соответствующие частные производные, т.е.

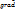f(M) = (, ).

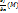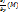Теорема: Градиент указывает направление наискорейшего возрастания ф-ии, а максимальная скорость этого возрастания равна модулю градиента

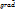Док-во: В силу равенства (M)=( f(M), ) имеем (M) =| 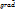f(M)|* 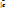|*cosγ (1), где γ – угол между вектором градиента и направлением .

C другой стороны, =1, а cos γ≤1. Следовательно, из (1) имеем

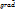(M) ≤| f(M)|

В случае γ=0 из (1) получим, что производная по направлению в точке М совпадает с градиентом.

10. Дайте определение однородной функции степени α

Ответ: Функция f(x,y) называется однородной функцией степени α, если при всех t выполняется тождество f(tx,ty)=t^kf(x,y)

Дата добавления: 2015-10-23