Space-time bending: the effect of gravity substance, the light rays to bend towards each other, bend space-time.

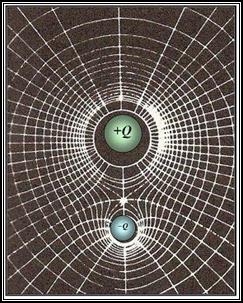
Different sizes, but at the same gravity pull each other showing the electromagnetic force fields the two electrons. {James Clerk Maxwell, 'Treatise on Electricity and Magnetism', 1873's book.}

A reclusive English gentleman named Henry Cavendish set out to use the same method to measure the force of gravity directly. Instead of two lightweight spheres at the end of the stick, he used two heavy ones, and attracted one of them by a third sphere, a big one. The force was tiny and because of the big masses, the instrument reacted agonizingly slowly. But in 1796, he finally succeeded--showing that not just the sphere of the Earth, but even spheres of lead in the lab, exerted a measurable force of gravity.

Thus for a while it seemed that three major forces in Nature--magnetic, electric and gravity--all obeyed the inverse squares law. Some differences existed--magnetic poles always came in pairs, and unlike the other two forces, which could both attract and repel, gravity could only attract. Nature seemed remarkably symmetric--until 1820, when Oersted and Ampйre showed that magnetism was really quite, quite different.

(Optional Extensions of the Theory – For Readers who have more skills and therotical knowledge )

Newton's formula for the gravitational attraction between mass m and mass M, at a distance r, is

F = G M m / r²

G ("big gee") is known as the gravitational constant, but Newton did not know that number. All he knew was the acceleration g ("little gee") at the Earth's surface, about 9.81 m/s²

^{What is the relation between G and g?}

^{--The weight of mass m is mg Newtons, and that should be equal to the pull of the Earth, if its mass M were concentrated in its center. Let R be the radius of the Earth. Then mg = G M m / r2}

^{so g = G M / r2}

^{Here G was measured by Hentry Cavendish, using a very refined version of a method developed for measuring electric and magnetic forces (if interested, see section on Coulomb's torsion balance in "A Millennium of Geomagnetism"). It is a very difficult measurement, because G is so small: by the above formulas, if you put m = M = 1 kilogram, r = 1 meter, you find that G is essentially the gravitational pull (in Newtons) between two masses of 1 kg, separated by 1 meter. That is a tiny, tiny force.}

^{Problem: If the mass density of Earth is D kg/meter3, express g (1 meter3 of water weighs 1000 kg, so D will amount to a few thousands).}

^{The volume of a sphere of radius R is (4π/3)R3, so its mass M is (4π/3)DR3, and we get}

^{g = G (4π/3)DR3 / R2 = (4π/3) G D R}

^{Suppose next that the density D of the Earth was constant throughout its volume, but its radius shrank to 1/4. What would this do to the gravity on the surface of this "smaller earth"?}

^{There would be less mass pulling down objects on the surface--but the surface would also be closer to the center of attraction! Still, as the above formula shows, the first factor outweighs the second.}

^{By the formula, if R → R/4, then g → g/4}

^{Gravity would decrease to 1/4 of its existing strength. The mass of the Moon (derived from its effect on the Earth's motion in space) is 0.012307 times the mass of the Earth, while its radius (measured by telescope) is 0.2725 Earth radii.}

^{How does g', the gravitational acceleration on the surface of the Moon, compare to g, the acceleration at the surface of Earth? In other words, how would the weight mg' of an object on the Moon compare to its weight mg on Earth? (Use a calculator, of course.) The weight of mass m on the Moon is}

^{mg' = G (0.012307 M) m /(0.2725 R)2
= [0.012307/(0.2725)2] G M m / R2
= (0.012307/0.74256) mg = 0.16574 mg}

^{Divide both sides by 0.16574}

^{6.034 g' = g}

^{RESULT : So g at Earth is about 6 times stronger.}

Chapter VII

Дата добавления: 2015-10-23