Rotational motion

Thus far we have focused on linear motion. Next we move to the consideration of rotational motion. The simplest kind of rotational motion is an object moving in a perfect circle at a constant speed. This is called uniform circular motion. The first step in describing uniform circular motion is to find rotational variables that are analogous to the linear variables of motion.

Consider the circle below:

When an object moves around the circumference of a circle a distance Δ s, this distance corresponds to the angle that is swept out by the motion, Δθ, and has the following relationship:

Δ s = r Δθ

This is the definition of an angle in radians, and for this relationship to hold, the angle must be represented in radians (rather than in degrees). The velocity or, to be precise, the speed is the rate of change of the arc length Δ s, and can be expressed as an equation involving the rate of change of the angle, Δθ:

v =Δ s/ Δ t = r Δθ/Δ t = r ω

ω =Δθ/Δ t

In these equations, ω is the rate at which the angle θ changes and is called the angular velocity or angular frequency. The velocity vector is tangent to the circle and points in the direction of the displacement; as a result, as long as the displacement changes, the velocity vector also changes.

The time it takes for the object to complete one complete turn around the circle is called the period and is denoted by T. The period is equal to the total distance traveled in one cycle divided by the velocity. Since we know the total distance around a circle (the circumference), the period can easily be related to either the velocity or the angular velocity:

T=2πr/ v

=2πr/ω

The frequency, denoted f, is defined as 1 divided by the period, which is the number of rotations the object undergoes in a certain time interval. It is related to the angular velocity as indicated in the equations:

f = 1/ T

=ω/2π

ω = 2π f

Recall that acceleration is the change in velocity with respect to elapsed time. Since velocity is a vector, any change in its magnitude (speed) or its direction involves acceleration. Thus far we have focused on cases in which only the magnitude of the velocity changed, but in uniform circular motion, the magnitude is constant and the direction changes constantly. This change results from a type of acceleration known as centripetal acceleration and written as a c. The centripetal acceleration always points inward, toward the center of the circle of motion, and is given by the equation

a _c = v ²/ r

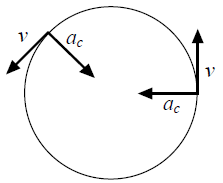
Centripetal acceleration is an important concept that is useful in describing many phenomena, such as the orbits of the moon and planets, and the motion of roller coasters. Whenever working with problems involving circular motion, remember that centripetal acceleration is an acceleration, not a force, and thus belongs on the m a side of the equation F = m a. Students (and occasionally even instructors) are sometimes tempted to include a separate centripetal force on the left side of the equation. However, whatever force it is that holds the object rotating in a circle is in fact a centripetal force and no additional separate force by that name is involved.

Centripetal acceleration is also the subject of another misconception. Passengers on quickly rotating rides in amusement parks feel like they are being thrown outward and often call this apparent push centrifugal force. In fact the force that people interpret as being thrown outward is a direct result of Newton’s first law. If at some point in its rotation a rotating body is released from whatever constrains it to rotate, it will move in a straight line, which will take it farther from the center of the circle. Thus, the feeling is one of being thrown outward. In fact, force is required to keep a rotating body moving in a circle. This force – no matter what provides it – is the centripetal force. Centrifugal force is a fictitious force and should never appear in calculations.

As shown above, the angular counterparts of position and velocity are angle, θ, and angular velocity, ω. The angular counterpart for acceleration is known as the angular acceleration, α, and is simply the rate of change of the angular velocity. The analogous linear and angular quantities can be summarized as follows:

Please note that the angular acceleration relates to the speed-changing part of the acceleration a _||. (This is the component of acceleration that is parallel to the direction of motion.) In rotational motion, the centripetal acceleration element, a_c is always present (even when the angular acceleration is 0); the centripetal acceleration element is perpendicular to the velocity, and is the direction-changing part of the acceleration. Because of the direct analogy between translational and rotational motion, it is straightforward to change our constant acceleration equations to describe rotational motion as follows:

The rotational kinematics equations are used in the same way the translational ones are. It is worth noting that, just like velocity and acceleration, the angular velocity and angular acceleration are actually vector quantities. (θ is not a vector because rotations around different axes do not commute. However, for our purposes this is not a great concern.) The direction of ω and α is just the direction of the axis about which they rotate. (An axis can have either of its two directions, and the direction of the angular velocity and acceleration is positive when the rotation is counterclockwise.)

The rotational counterpart of force is torque. Forces cause translational motion and torques produce rotational motion. The translational statement of Newton’s second law is that the net force acting on an object is equal to the mass (inertia) times the acceleration (change in the object’s translational motion with respect to time). There is also a rotational version of Newton’s second law, which is the net torque on an object, τ, is equal to the object’s rotational inertia, I, times its angular acceleration, α. These equations are shown side by side below for comparison.

Just as the mass of an object is a measure of how difficult it is to start an object moving, the rotational inertia I of an object is a measure of how difficult it is to start the object turning or rotating. The value of I depends not only on the mass, but also on the distribution of the mass. We discuss the computation of I below.

Torque depends on three basic quantities: (1) the applied force F, (2) the location where it is applied, r (relative to the pivot point) and (3) the direction in which it is applied.

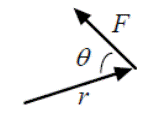
The formula for torque is:

τ = rF sinθ

and its units are newton-meters or N·m. (Note: While one Joule is equal to one newton·meter, torque is expressed only in terms of newton-meters, not Joules.) The formula for torque can be best understood by considering an example, for instance, turning a bolt, door, or merry-go-round. The object moves farther when a larger force is applied or when a force is applied farther from the pivot point. But how does torque correspond to the angle at which the force is applied? Imagine exerting a force on a bolt or a merry-go-round. If the force is parallel to the radius vector, it acts on the pivot point and no rotation results. By contrast a force applied at an angle perpendicular to the radius vector has its greatest turning effect and thus creates a large torque.

It is often useful to associate all the angular dependence with either the force or the position vector, either by finding the component of force perpendicular to the radius, or by finding the component of radius perpendicular to the force, as illustrated below. With this approach, the torque can be calculated by using the perpendicular component, which simplifies calculations.

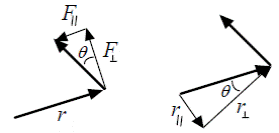
The perpendicular component of the radius is used so often that it has a special name, the lever arm. Torque is a vector quantity and is equal to the cross product of the position and force vectors. From our previous review of cross products, we know that this operation yields exactly the equation we have been seeking, an expression for the magnitude of the torque;

τ = r Ч F

τ = rF sin θ

The simplest kind of rotational problem is one in which the sum of the torques, and thus the angular acceleration, is 0:

Σ τ = I α = 0

α = 0

Such problems are called rigid-body or equilibrium problems.

(Some Useful Optional Equations of the Theory)

Where R is the distance between the two axes, and M is the mass of the object. A brief list of useful moments of inertia follows.

Once we know the moment of inertia, torque problems are solved almost identically to force problems. The same steps used force problems and for static torque problems are applied, but instead of setting the angular acceleration to 0, it is left as a variable that must be determined.

Many rotational dynamics problems can be solved in several ways. For example, objects rolling down a hill can be treated as a combination of translational motion and rotational around the center of mass, or as purely rotational motion around the point of contact. Kinetic energy and momentum also have rotational counterparts. The translational kinetic energy analog is rotational kinetic energy, and the equations for the two are shown below for comparison.

The applications of rotational kinetic energy are fairly straightforward. It is simply another form of energy. The rotational counterpart of momentum is angular momentum (L). It can be represented and applied in a variety of ways. For a point object, the angular momentum is the cross product of the radius and the momentum:

L = r Ч p

L = rp sinθ = mrv sinθ

Notice that angular momentum is a vector quantity, though in introductory courses its vector nature is rarely important. For a rotating rigid body angular momentum can be written in a form analogous to the formula for momentum.

The vector nature of angular momentum of a rigid body can become very complex and is beyond the scope of this course. The analog of force being the rate of change of momentum, is that torque is the rate of change of angular momentum.

Thus, just as momentum is conserved in the absence of external forces, angular momentum is conserved in the absence of external torques. This is known as the conservation of angular momentum.

In the same way that the principle conservation of linear momentum can be, the principle of conservation of angular momentum can be used in collisions (including cases with external forces, but no external torques). It can also be applied to a variety of other circumstances. For example, both an object moving in a straight line at a constant velocity and an object moving in uniform circular momentum have constant angular momentum. A variety of other motions have constant angular momentum, and this characteristic is useful in describing the orbits of planets. Another example of the principle’s use is that of an ice-skater: when she pulls in her hands she reduces her moment of inertia, and thus her angular velocity increases to maintain constant angular momentum. Notice that this results in an increase in rotational kinetic energy, which comes from the work the skater must perform in pulling in her hands..

§ § §

~ END of BOOK ~

Bibliography

Printed Books

NEWTON, ISAAC “MATHEMATICAL PRINCIPLES of NATURAL PHILOSOPHY and SYSTEM of THE WORLD” Florian CAJORI, University of California Press, Berkeley California 1960

EINSTEIN, Albert “THE MEANING of RELATIVITY”, Princeton University Press, Princeton New Jersey 1966

BACON, Francis “True directions concerning the interpretation of nature”, Academic Lectures, 1605

KANT, Immanuel “Kant-Laplacesche Theorie der Planetenentstehung”, Nova dilucidatio“, Immanuel Kant: AA I, 385–416

THOMAS, George B., WEIR, HASS, GIORDANO, “THOMAS’ CALCULUS”, 11th Edition, Addison & Wessley, 2004

MANKIEWICZ, Richard “HISTORY OF THE MATHEMATICS”, Second edition, Addison Wesley, Usa 2006

Дата добавления: 2015-10-23