Задание 3. «Обобщенные характеристики сигналов и каналов».

Таврический национальный университет имени В.И. Вернадского

Физический факультет

Кафедра компьютерной инженерии и моделирования

Практические задания и методические рекомендации

по дисциплине «Теория информации и кодирования»

Для студентов специальности 7.05010201 – Компьютерные системы и сети

(Институт последипломного образования)

Симферополь, 2011

Задание 1. «Количество информации и неопределенность сообщения».

На вход информационного устройства подается совокупность сообщений {x_k}, k=1¸N. Вероятности сообщений задаются в виде счетчика случайных чисел. Определить среднее количество информации в совокупности сообщений {x_k} и максимальную энтропию сообщений.

№ варианта

N

Методические указания:

Вероятности сообщений на входе должны удовлетворять свойству:

Среднее количество информации в совокупности сообщений:

Максимальная энтропия сообщений:

Задание 2. «Количество информации при неполной достоверности сообщений».

На вход информационной системы с помехами поступает совокупность дискретных сообщений {x_k}, k=1¸N. Вероятность сообщений на входе задается в виде счетчика случайных чисел. Вероятность безошибочной передачи сообщений составляет не менее 70 %. Вероятность ошибочной передачи задается в виде счетчика случайных чисел. Определить количество информации, получаемое при неполной достоверности сообщений.

№ варианта

N

Методические указания:

Вероятности сообщений на входе должны удовлетворять свойству:

Вероятность безошибочной передачи:

.

Вероятность переходов i-го сообщение на выход подчиняется свойству:

Количество информации при неполной достоверности сообщений:

Энтропия на входе H(X) и остаточная энтропия H(X/Y):

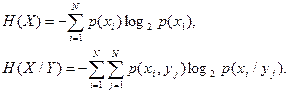
Совместная вероятность p(x_i, y_j):

Вероятность на выходе:

.

Задание 3. «Обобщенные характеристики сигналов и каналов».

Источник информации вырабатывает информационный сигнал с N различными символами. Длительность символов t_i задается в виде счетчика случайных чисел в диапазоне [1– N] мс. Вероятности появления на входе p(x_i) даются в виде счетчика случайных чисел.

Источник информации подключен к каналу передачи сигналов.

Определить:

1. пропускную способность канала и скорость передачи информации при использовании канала без помех;

2. пропускную способность канала и скорость передачи информации в канале с помехами с учетом того, что вероятность перехода одного сигнала в другой (вероятность ошибки в канале) .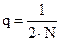

№ варианта

N

Методические указания:

Пропускная способность канала без помех:

где - скорость передачи элементарных символов сигнала; средняя длительность элементарных сигналов.

Скорость передачи информации в канале без помех:

где энтропия .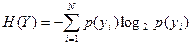

Пропускная способность канала с помехами:

Скорость передачи информации в канале с помехами:

Остаточная энтропия H(Y/Z) рассчитывается как и в задании 2.

Задание № 4. «Помехоустойчивое кодирование. Систематический код.»

Задано количество информационных разрядов (k). Построить систематический код, позволяющий обнаруживать и исправлять однократные ошибки.

Отчет и программа должны содержать:

1. производящую матрицу;

2. проверочную матрицу;

3. исходный информационный сигнал;

4. построенный систематический код;

5. соответствие позиции ошибки и вида синдрома;

6. код с ошибкой;

7. определение позиции ошибки.

№ варианта

k

Методические указания:

Минимальное кодовое расстояние

, где s - кратность обнаруживаемых и исправляемых ошибок.

Определение значности кода (длины кодовой комбинации n):

.

Количество проверочных разрядов

.

Производящая матрица P_n,k имеет вид:

Информационная подматрица U_k выбирается в качестве квадратной единичной матрицы:

.

Требования к проверочной подматрице Н_р:

1. Количество единиц в строке должно быть не менее d_min-1.

2. Сумма по модулю два двух любых строк должна содержать не менее d_min-2 единиц.

Подматрица H¹ имеет вид:

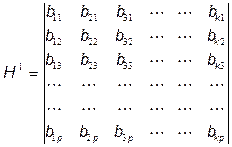
Проверочная матрица имеет вид:

.

Алгоритм определения проверочных символов по информационным с помощью подматрицы H¹ следующий. Позиции, занимаемые единицами в первой строке подматрицы H¹, определяют информационные разряды, которые должны участвовать в формировании первого проверочного разряда кодовой комбинации. Позиции единиц во второй строке подматрицы Н¹ определяют информационные разряды, участвующие в формировании второго проверочного разряда и т. д.

Расположение символов в систематическом коде:

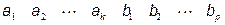
Проверочная матрица Н используется для определения места ошибки в кодовой комбинации, а, следовательно, исправления ошибок. Проверка кодовых комбинаций при этом выполняется путем суммирования по модулю два проверочных символов кодовых комбинаций и проверочных символов, вычисленных по принятым информационным. В результате будет получена совокупность контрольных равенств, каждое из которых представляет сумму по модулю два одного из контрольных символов и определенного количества информационных.

Состав контрольных равенств легко определяется из проверочной матрицы H. В состав первого контрольного равенства должны входить символы, позиции которых заняты единицами в первой строке матрицы H. В состав второго контрольного равенства должны входить символы, позиции которых заняты единицами во второй строке матрицы H, и т. д.

В результате р таких проверок будет получено р-разрядное двоичное число (синдром), которое будет равно нулю при отсутствии ошибок и отлично от нуля в случае наличия ошибок.

Если код предназначен для исправления ошибок, то должно быть заранее определено соответствие между видом синдрома и видом исправляемой ошибки.

Задание № 5. «Помехоустойчивое кодирование. Код Хэмминга.»

Задано количество информационных разрядов (k). Построить код Хэмминга, позволяющий обнаруживать и исправлять однократные ошибки.

Отчет и программа должны содержать:

1. исходный информационный сигнал;

2. построенный код Хэмминга;

3. код с ошибкой;

4. определение позиции ошибки.

№ варианта

k

Дата добавления: 2015-10-29