Спектр сигнала.

В далеком 1822 году французским математиком и физиком Жан Батист Жозефом Фурье была опубликована монография «Аналитическая теория тепла». В этом труде, предлагалось представлять функции в виде тригонометрических рядов. В чем же смысл такого представления?

Предполагается, что исходный сигнал является суммой синусоидальных колебаний (такого рода колебания называют гармоническими, а сами колебания – гармониками) различной частоты, амплитуды и фазы. Грубо говоря, результат (коэффициенты) преобразования Фурье исходного сигнала, показывает какие гармоники, и какой интенсивности участвуют в формировании этого сигнала. Иными словами, отображает спектр исходного сигнала.

Данное преобразование стало весьма популярным в задачах обработки звуковых сигналов, поскольку любой звук является композицией тонов определенной частоты и интенсивности (напомним, что тон – есть гармоническое колебание). Следовательно, данное преобразование, при определенных условиях, способно достаточно точно отобразить состав того или иного звука.

В Matlab существует блок, который позволяет наглядно увидеть спектр сигнала, полученный с помощью преобразования Фурье.

3.1 Настройка блока «Signal Processing Blockset \ Signal Processing Sinks \ Spectrum scope».

Данный блок имеет 4 вкладки.

Вкладка Scope properties:

Spectrum units – выбор шкалы (линейная или логарифмическая) и типа измеряемых данных (Мощность компонент Ватах или децибелах). Оставляем логарифмическую шкалу, и единицы измерения – мощность в децибелах, то есть dBW/Hertz.

Spectrum type – преобразование Фурье отображает спектр, симметричный относительно нуля. Данный параметр, позволяет либо показывать (если выбрать значение Two-sided), либо не показывать (если выбрать значение One-sided) симметричную отрицательную часть спектра. Значение оставляйте по своему выбору.

Buffer input – Поскольку преобразование Фурье выполняется над определенной выборкой отсчетов исходного сигнала, а «SineWave» на выходе генерирует скалярные величины (отсчеты), то перед тем как применять преобразование, необходимо накопить массив отсчетов. Для этого выберите данную опцию (поставив галочку). Появятся два поля:

Buffer size и Buffer overlap. Первый параметр определяет число отсчетов, которые будут накоплены перед тем, как применять преобразование Фурье. Второй параметр определяет число последних отсчетов из предыдущего буфера, включенных в текущий.

Buffer overlap выставляйте равным 0. Buffer size выставляйте исходя из следующих условий:

1. Для адекватного представления спектра с помощью преобразования Фурье необходимо, чтобы длительность сигнала (число накопленных в буфер отсчетов N умноженное на интервал дискретизации Tд) была больше периода компоненты с самой низкой частотой. Например, если в вашем сигнале компонента с наименьшей частотой 10Гц, и частота дискретизации 0.02, то, по меньшей мере, необходимо взять N=1/(F*0.02)+1=6 отсчетов.

2. Поскольку в блоке осуществляется быстрое преобразование Фурье, то число отчетов, накапливаемых в буфере должно быть кратно 2ⁱ, то есть 2, или 4, или 8, или 16, или 32 и т.д. Применительно к предыдущему примеру (N=6), в поле Buffer size минимальное значение равно 8. Можете взять больше отсчетов и пронаблюдать результат.

Следующие два параметра относятся к оконной функции, применяемой при преобразовании. Их оставляйте по-умолчанию:

Window – Значение «Hann».

Window sampling – Значение «Periodic».

Specify FFT length – Используется, если в буфер заносится большее число отсчетов, а преобразование осуществляется над меньшим их числом. Галочку не ставьте!

Number of spectral averages – Используется для усреднения спектра. Поскольку исходный сигнал у нас периодичен во времени, отключаем усреднение, установив значение «1».

Остальные вкладки оставляем без изменений.

Методические указания­­­­­­­

Сохраняйте отдельную модель для каждого пункта!

1. Создать модель, для генерации и наблюдения непрерывного сигнала по варианту (см. таблицу ниже). Для сложения использовать блок «Simulink \ Commonly used blocks \ Sum». Генератор синусоидального колебания – «Simulink \ Sources \ SineWave». Для вывода сигнала использовать виртуальный осциллограф «Simulik \ Sinks \ Scope». Подберите время моделирования такое, чтобы на осциллографе отображалось 5 колебаний сигнала.

При вычитании синусоиды, используйте так же сумматор, но, либо в значение амплитуды генератора синусоиды записывайте отрицательное значение, либо добавляйте в сумматоре интерфейс для вычитания, а не суммирования.

№ Варианта	Сигнал
1, 11, 21
2, 12, 22
3, 13, 23
4, 14, 24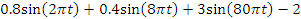
5, 15, 25
6, 16, 26
7, 17, 27
8, 18,28
9, 19, 29
10, 20, 30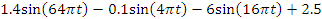

2. Использовать модель из предыдущего пункта, но настроить блоки для симуляции дискретного сигнала.

2.1. Моделирование проводить для периода дискретизации порядка 0.0001.

2.2. Моделирование проводить для периода дискретизации, выбранного в соответствии с теоремой Котельникова.

Внимание! Выбранная частота дискретизации должна быть одинаковой у всех блоков модели.

3. Используя модель предыдущего пункта, с помощью блока «Signal Processing Blockset \ Signal Processing Sinks \ Spectrum scope» пронаблюдать спектр дискретного сигнала (частота дискретизации выбиралась по теореме Котельникова).

Поскольку исходный сигнал является суммой гармонических функций (синусов), то частоты пиков отображаемого блоком «Spectrum scope» графика должны совпадать с частотами синусов исходного сигнала.

По картинке определить частоту гармоник исходного сигнала, сравнить полученные результаты с исходными данными, сделать вывод о достоверности полученных результатов.

Дата добавления: 2015-10-29