Дискретизация сигнала.

Задание.

1. Произвести дискретизацию одного из сложных сигналов.

2. Исследовать спектры исходного и дискретизированного сигналов.

3. Исследовать частотные и импульсные характеристики фильтров-восстановителей.

4. Исследовать процесс восстановления дискретизированных сигналов.

Дискретизация сигнала.

Для дискретизации и восстановления возьмем сигнал s1(t), который представляет собой сумму двух гармоник с частотами 2.38 и 4.76 кГц. Осциллограмма этого сигнала представлена на рисунке ниже.

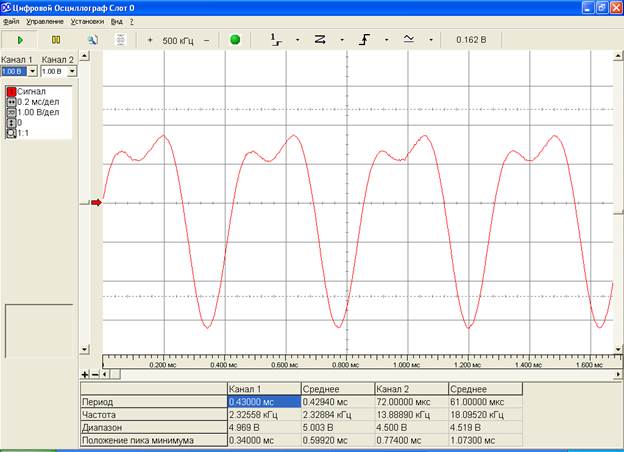
Рис.1. Осциллограмма сигнала s1(t).

Известно, что любой периодический сигнал x(t) можно представить в виде суммы гармонических колебаний с частотами, кратными основной частоте f=1/T, и с некоторыми амплитудами. Совокупность таких амплитуд образует амплитудный спектр сигнала. Линейчатый амплитудный спектр исследуемого периодического сигнала изображен на рис.2 и рис.3.

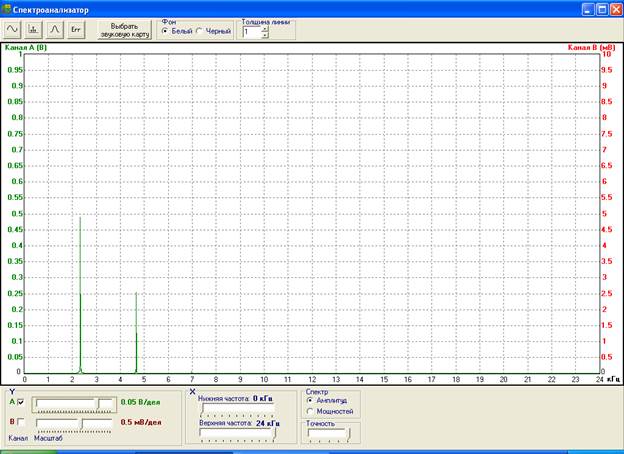
Рис.2. Спектр сигнала s1(t).

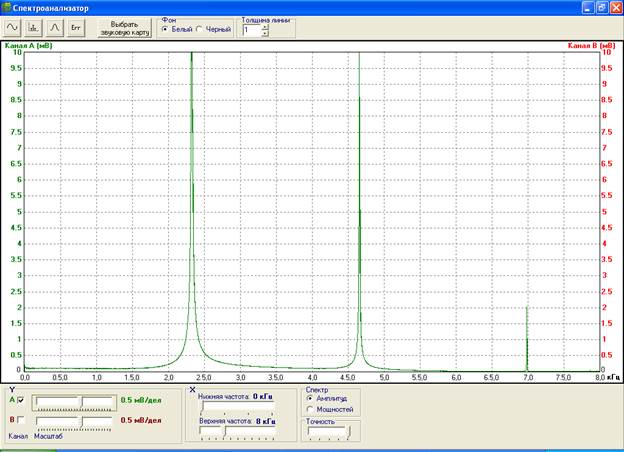
Рис.3.Спектр сигнала s1(t).

Проанализируем спектр сигнала s1(t). Основная частота составляет f=2.38 кГц. Ей соответствует гармоника с амплитудой 0.48 В. Из рис.2 и рис.3 также можно сделать вывод, что составляющими сигнала s1(t) являются гармоники с частотами 2f=4.76 кГц и 3f=7.14 кГц и соответствующими амплитудными значениями в 0.25 и 0.002 В.

Теперь положим значение верхней частоты Fв исследуемого сигнала s1(t), равное 14 кГц. Тогда из соотношений ∆t=1/fд=1/2Fв, где ∆t – временной интервал между соседними отсчетами дискретизированного сигнала, fд – частота дискретизации, получим, что fд=2Fв.

В нашем случае имеем fд=2*14=28 кГц. Так как на сменном блоке отсутствует значение частоты дискретизации в 28 кГц, то выберем из значений на сменном блоке наиболее близкое к полученному, т.е. fд=24 кГц.

Сравним спектры исходного (рис.2 и рис.3) и дискретизированного сигналов при разной частоте дискретизации.

При частоте дискретизации 24 кГц исходный и дискретизированный сигналы выглядят следующим образом:

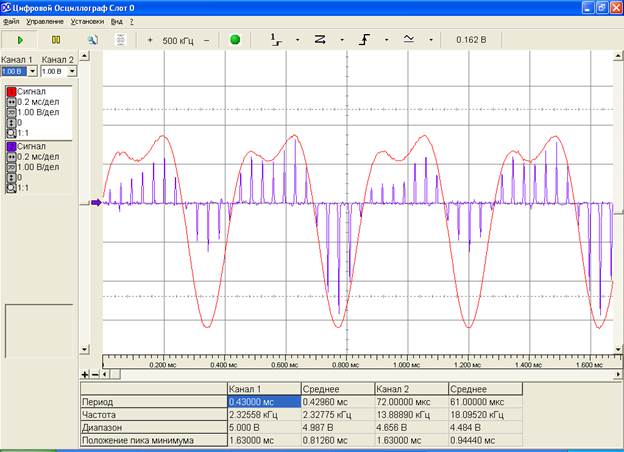
Рис.4. Осциллограмма исходного s1(t) (красный цвет) и дискретизированного s1(k∆t) (синий цвет) сигналов (частота дискретизации – 24 кГц).

Из рис.4 видно, что дискретизированный сигнал представляет собой набор приближенных значений сигнала s1(t) в моменты времени k∆t, где k – целое число.

При этом напряжение дискретизации изменяется следующим образом (рис.5):

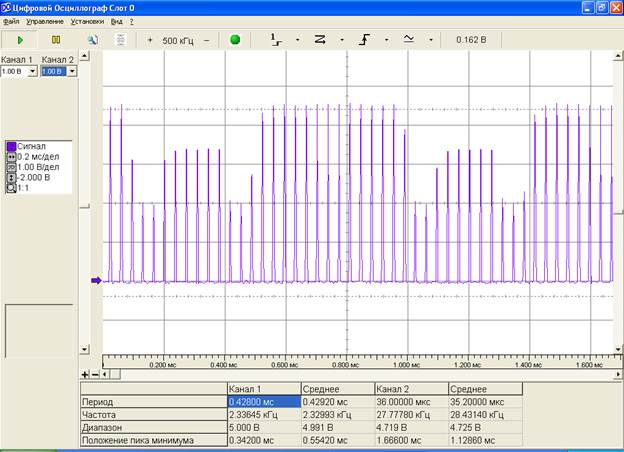
Рис.5. Напряжение дискретизации (частота дискретизации – 24 кГц).

Повысим частоту дискретизации до 48 кГц. Тогда исходный и дискретизированный сигнал будут выглядеть следующим образом (рис.6):

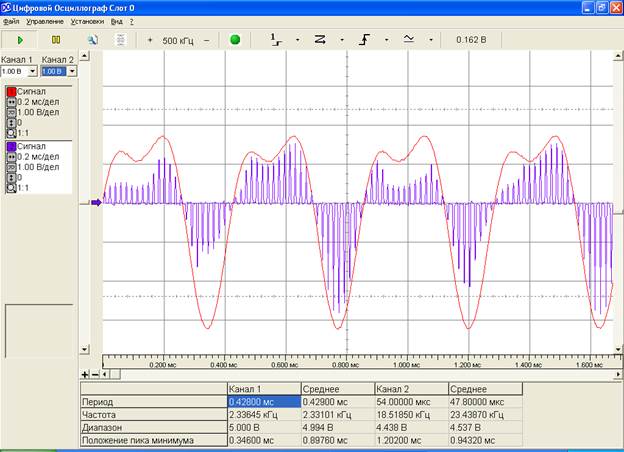
Рис.6. Осциллограмма исходного s1(t) (красный цвет) и дискретизированного s1(k∆t) (синий цвет) сигналов (частота дискретизации – 48 кГц).

Сравнивая рис.6 с рис.4 видно, что дискретизированный сигнал тем больше соответствует по значениям k∆t сигналу s1(t), чем больше частота дискретизации.

Спектр дискретизированного сигнала представлен на рис.7 и рис.8.

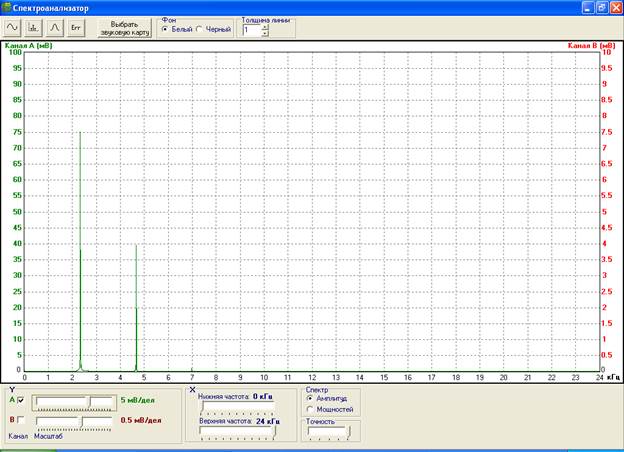
Рис.7. Спектр дискретизированного сигнала s1(k∆t) (частота дискретизации – 48 кГц).

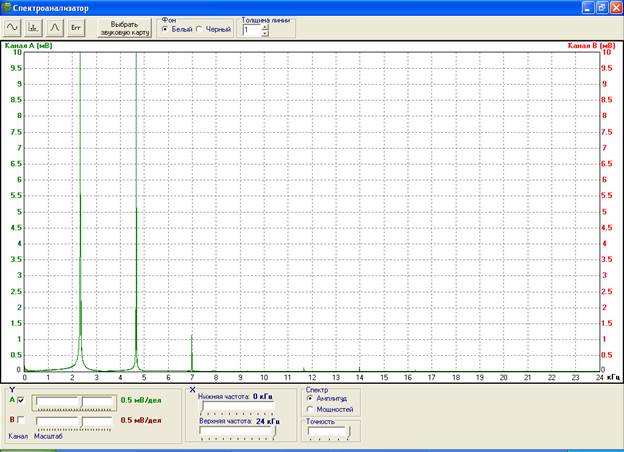
Рис.8. Спектр дискретизированного сигнала s1(k∆t) (частота дискретизации – 48 кГц).

Уменьшим частоту дискретизации до 16 кГц. Получаем следующую картину (рис.9):

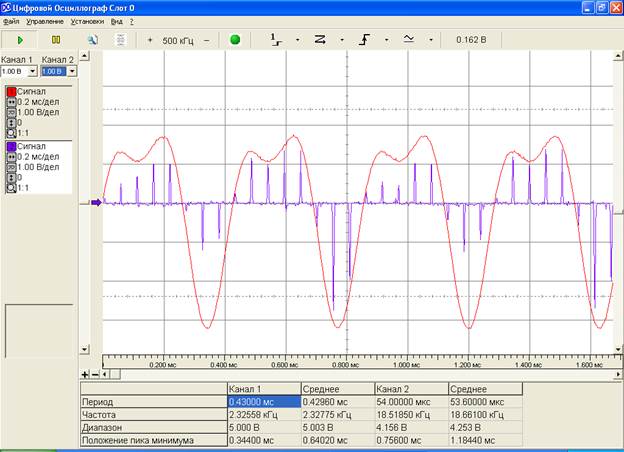
Рис.9. Осциллограмма исходного s1(t) (красный цвет) и дискретизированного s1(k∆t) (синий цвет) сигналов (частота дискретизации – 16 кГц).

Сравнивая рис.9 с рис.4 и рис.6 видно, что дискретизированный сигнал тем меньше соответствует по значениям k∆t сигналу s1(t), чем меньше частота дискретизации.

Спектр дискретизированного сигнала изображен на рис. 10 и рис. 11:

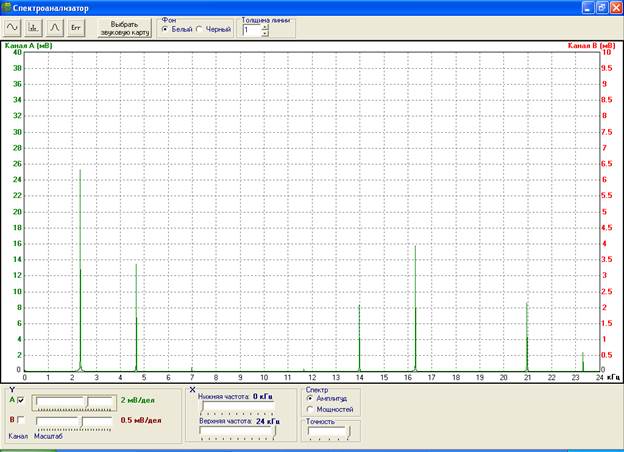
Рис.10. Спектр дискретизированного сигнала s1(k∆t) (частота дискретизации – 16 кГц).

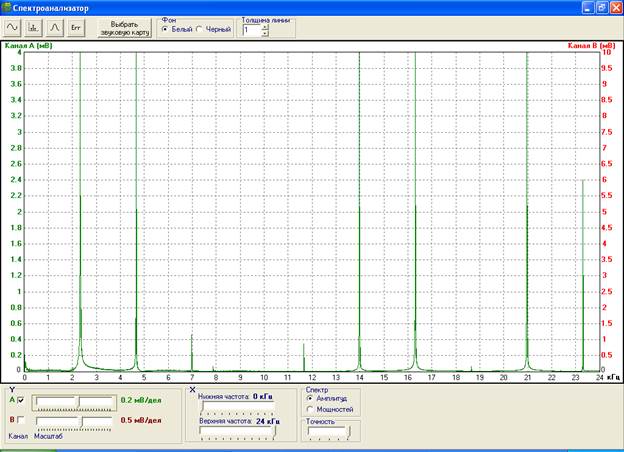
Рис.11. Спектр дискретизированного сигнала s1(k∆t) (частота дискретизации – 16 кГц).

Сравнивая рис.10, рис.11, рис.7 и рис.8 с рис.2 и рис.3 можно сделать вывод, что спектр дискретизированного сигнала тем больше совпадает со спектром ихсодного сигнала, чем выше частота дискретизации. При этом частоты несущих гармоник остаются неизменными, и изменяются только их амплитуды.

Дата добавления: 2015-10-29