
Читайте также:
|
В турбинных ступенях могут быть принципиально применены те же законы закрутки, что и в компрессорных ступенях (-1,0< m <1,0). Однако условие отсутствия отрицательной реактивности у корня и сильной закрутки лопатки по высоте ограничивают диапазон возможного изменения показателя степени m в турбинных ступенях. При сильно закрученных лопатках существенно усложняется технология изготовления их, так как турбины в современных авиационных двигателях в основном выполняются охлаждаемыми, со сложными внутренними полостями. Избежать отрицательной реактивности у корня в некоторых случаях возможно за счет увеличения реактивности на среднем диаметре. Однако максимально возможный допустимый диапазон изменения реактивности на среднем радиусе достаточно узок ( ) из-за сильного роста степени реактивности в верхних слоях и соответствующего увеличения потерь, обусловленных радиальным зазором. Стремление избегать отрицательной степени реактивности у корня уменьшением показателя m до m = -1 (m = -1 – ступень с постоянной степенью реактивности) приводит к необходимости иметь на выходе из рабочего колеса значительные окружные составляющие абсолютной скорости
) из-за сильного роста степени реактивности в верхних слоях и соответствующего увеличения потерь, обусловленных радиальным зазором. Стремление избегать отрицательной степени реактивности у корня уменьшением показателя m до m = -1 (m = -1 – ступень с постоянной степенью реактивности) приводит к необходимости иметь на выходе из рабочего колеса значительные окружные составляющие абсолютной скорости  (т.е. угол
(т.е. угол  значительно отличный от 900). Поэтому применение показателя m <0 в турбинных ступенях нерационально, тем более что уже при m = 0 наблюдается значительная неравномерность поля осевых скоростей по радиусу. Таким образом, практическое применение в турбинных ступенях в основном находят два закона закрутки:
значительно отличный от 900). Поэтому применение показателя m <0 в турбинных ступенях нерационально, тем более что уже при m = 0 наблюдается значительная неравномерность поля осевых скоростей по радиусу. Таким образом, практическое применение в турбинных ступенях в основном находят два закона закрутки:
- закон постоянства циркуляции по радиусу (m = 1), для лопаток с  ;
;
- промежуточный закон ( ), т.е. закон постоянства угла выхода потока из соплового аппарата (
), т.е. закон постоянства угла выхода потока из соплового аппарата ( ).
).
При возможных значениях угла 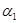 численное значение показателя
численное значение показателя  , лежит в пределах 0,65…0,85. Меньшие значения реализуются в ступенях с более длинными лопатками. Однако следует отметить, что в практике проектирования ступеней осевых турбин применяются иногда и другие законы закрутки.
, лежит в пределах 0,65…0,85. Меньшие значения реализуются в ступенях с более длинными лопатками. Однако следует отметить, что в практике проектирования ступеней осевых турбин применяются иногда и другие законы закрутки.
Расчетные сечения в корневых и периферийных частях можно вычислить по формулам
 ;
;
 ,
,
где 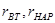 - втулочный и наружный радиусы проточной части колеса турбины. При конической проточной части под значениями
- втулочный и наружный радиусы проточной части колеса турбины. При конической проточной части под значениями  и
и  следует понимать их значения на входе в решетку. Определяются эти значения из чертежа меридионального сечения проточной части (см. рис. 3.1).
следует понимать их значения на входе в решетку. Определяются эти значения из чертежа меридионального сечения проточной части (см. рис. 3.1).
 - радиус переходной галтели (закругления) для корневого и периферийного сечения лопаток.
- радиус переходной галтели (закругления) для корневого и периферийного сечения лопаток.
Рекомендуется выбирать:
 при h >100 мм (h – высота лопатки);
при h >100 мм (h – высота лопатки);
 при h< 60 мм;
при h< 60 мм;
 - в 1,5…2 раза меньше, чем
- в 1,5…2 раза меньше, чем  .
.
Осевая составляющая абсолютной скорости потока газа на входе в рабочее колесо в расчетных сечениях по радиусу определяется по формуле
 , (5.12)
, (5.12)
где  - относительный радиус расчетного сечения;
- относительный радиус расчетного сечения;
 - периферийный радиус;
- периферийный радиус;
 - текущий расчетный радиус.
- текущий расчетный радиус.
Для случая, когда m = 0, предыдущее уравнение будет иметь вид
 (5.13)
(5.13)
Для закона m = 1
 . (5.14)
. (5.14)
Осевая составляющая абсолютной скорости потока на выходе из рабочего колеса
 (5.15)
(5.15)
Для m = 0 предыдущее уравнение имеет вид
 (5.16)
(5.16)
Для закона m = 1
 . (5.17)
. (5.17)
С учетом использования ЭВМ в расчетах окружные составляющие абсолютной скорости на входе и выходе из рабочего колеса ступени удобно представлять в виде
 , (5.18)
, (5.18)
 , (5.19)
, (5.19)
где  ;
;
 .
.
Для закона 

 ,
,
 .
.
Дальнейший порядок расчета и расчетные формулы не зависят от выбранного закона закрутки и могут быть представлены в табличном виде (табл. 5.2).
Численные значения, приведенные в табл. 5.2, относятся к расчету параметров по высоте рабочей лопатки первой ступени турбины хххххх для которой выбран закон закрутки  .
.
Таблица 5.2
| Определяемый параметр и расчетные формулы | Раз-мерн. | Относительный радиус сечения | ||

| 
| 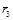
| ||
Относительный радиус расчетного сечения 
| ||||
Осевая составляющая скорости 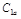 на входе в рабочее колесо [расчетная формула (5.12)…(5.14)] на входе в рабочее колесо [расчетная формула (5.12)…(5.14)]
| 
| |||
Осевая составляющая скорости  на выходе из рабочего колеса [расчетная формула (5.15)…(5.17)] на выходе из рабочего колеса [расчетная формула (5.15)…(5.17)]
| 
| |||
Вспомогательные расчетные величины

| 
| |||

| 
| |||
Окружная составляющая скорости воздуха  на входе в рабочее колесо [расчетная формула (5.18)] на входе в рабочее колесо [расчетная формула (5.18)]
| 
| |||
Окружная составляющая скорости воздуха  на выходе из рабочего колеса [расчетная формула (5.19)] на выходе из рабочего колеса [расчетная формула (5.19)]
| ||||
Для закона  (m =1,0) (m =1,0)
| ||||
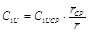
| 
| |||

| 
| |||
Абсолютная скорость воздуха на входе в колесо 
| 
| |||
То же на выходе из колеса 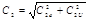 1) 1)
| 
| |||
Приведенная скорость потока на входе в колесо при  
| ||||
Тоже на выходе из колеса при 

| ||||
Окружная скорость колеса на входе 
| 
| |||
Тоже на выходе 
| 
| |||
Угол входа потока в решетку рабочих лопаток в относительном движении 
| град | |||
Угол выхода потока из решетки рабочих лопаток в относительном движении 2)

| град | |||
Угол поворота потока в решетке рабочего колеса 
| град | |||
Относительная скорость потока на входе в рабочую решетку 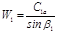
| 
| |||
Тоже на выходе из решетки 
| 
| |||
Угол потока на входе в рабочую решетку в абсолютном движении 
| град | |||
Тоже на выходе из решетки 3) 
| град | |||
Температура торможения в относительном движении 
| К | |||
Приведенная скорость в относительном движении на входе в колесо

| ||||
То же на выходе из колеса 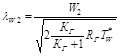
| ||||
Статическое давление на входе в колесо 4)

| Па | |||
Статическое давление на выходе из колеса 4) 
| Па | |||
Степень реактивности 4),5) 
|
1) При отрицательном значении  (
( >900) в расчетной формуле берется модуль значения
>900) в расчетной формуле берется модуль значения  .
.
2) При отрицательном значении  (
( >900) в расчетной формуле берется модуль значения
>900) в расчетной формуле берется модуль значения  и знак минус.
и знак минус.
3) При отрицательном значении  (
( >900) в расчетной формуле берется модуль значения
>900) в расчетной формуле берется модуль значения  , и определяется угол (1800 -
, и определяется угол (1800 -  ).
).
4) Скоростные коэффициенты  и
и  приняты постоянными по высоте.
приняты постоянными по высоте.
5) Степень реактивности у корня должна быть положительной или равной нулю. В случае отрицательной реактивности в корневом сечении необходимо применить другой закон закрутки (с меньшим значением m) или повысить реактивность на среднем радиусе. Если принять в корневом сечении  , то на среднем диаметре реактивность определится по формуле
, то на среднем диаметре реактивность определится по формуле
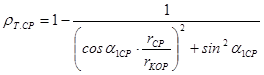
Однако значение  не должно превышать
не должно превышать  .
.
При изменении степени реактивности на среднем диаметре расчеты турбины по среднему диаметру необходимо скорректировать.
§5.5. Компрессорные решетки с большими углами поворота потока 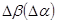
Проблема создания современных авиационных высоконагруженных компрессоров (с меньшим число ступеней) состоит в существенном увеличении нагрузки на ступень  при минимальном снижении КПД компрессора.
при минимальном снижении КПД компрессора.
Для перспективных многорежимных ГТД число ступеней компрессора газогенератора должно быть не более z = 5…6  , а значения КПД компрессора не ниже
, а значения КПД компрессора не ниже  .
.
Затраченный напор в ступени или работа, затрачиваемая на вращение лопаток рабочего колеса, определяется по формуле (см. §2.1, п.6)
 .
.
Таким образом, затраченный напор зависит от величины окружной скорости и разности окружных составляющих абсолютной скорости на выходе и входе в рабочие лопатки  . Последнее, в свою очередь, зависит от угла поворота потока в рабочем колесе
. Последнее, в свою очередь, зависит от угла поворота потока в рабочем колесе  . Поэтому высоконапорную ступень можно получить за счет высоких окружных скоростей или при заданных числах Маха в решетке за счет увеличения угла поворота потока в решетке
. Поэтому высоконапорную ступень можно получить за счет высоких окружных скоростей или при заданных числах Маха в решетке за счет увеличения угла поворота потока в решетке  .
.
Однако большие углы поворота  (более 20…30) приводят к повышенным потерям в таких решетках из-за диффузорного характера течения в них и появления срывных зон.
(более 20…30) приводят к повышенным потерям в таких решетках из-за диффузорного характера течения в них и появления срывных зон.
Диффузорность канала можно охарактеризовать углом раскрытия эквивалентного диффузора, который можно определить по формуле
 .
.
Очевидно, сохранить угол раскрытия диффузора в допустимых пределах  при больших углах
при больших углах  можно путем увеличения l – длины средней линии межлопаточного канала. А это приводит к увеличению хорды лопатки. Поэтому путь повышения напорности ступени за счет увеличения угла
можно путем увеличения l – длины средней линии межлопаточного канала. А это приводит к увеличению хорды лопатки. Поэтому путь повышения напорности ступени за счет увеличения угла  приводит к применению широкохордных лопаток, и как следствие, при заданном шаге, к большей густоте решетки.
приводит к применению широкохордных лопаток, и как следствие, при заданном шаге, к большей густоте решетки.
Например, на среднем радиусе  = 1,3…1,7.
= 1,3…1,7.
Удлинение широкохордных лопаток
 ,
,
где  - ширина решетки у корня лопатки.
- ширина решетки у корня лопатки.
В последних ступенях вентиляторов и компрессоров высокого давления, в случае использования в них высоконагруженных ступеней, часто требуются большие углы поворота потока в решетках их направляющих аппаратов  .
.
В подобных случаях, как показывают результаты экспериментальных исследований и опыт создания современных компрессоров, целесообразно использовать двухрядные решетки направляющего аппарата. Двухрядная решетка представляет собой две решетки, расположенные последовательно и имеющие определенные перекрытия по фронту и оси.
В основе обращения к двухрядным решеткам лежит идея о перераспределении энергии в межлопаточных каналах между различными областями потока.
Как показывают выполненные экспериментальные исследования, уровень потерь полного давления в двухрядных решетках 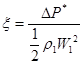 на номинальных режимах (в зависимости от густоты решеток
на номинальных режимах (в зависимости от густоты решеток  ) на 20%…10% выше уровня потерь в эквивалентных однорядных. Но на критических и сверхкритических режимах (т.е. при больших
) на 20%…10% выше уровня потерь в эквивалентных однорядных. Но на критических и сверхкритических режимах (т.е. при больших  ), уровень потерь в двухрядных решетках ниже, чем в эквивалентных однорядных решетках вследствие устранения срывных зон.
), уровень потерь в двухрядных решетках ниже, чем в эквивалентных однорядных решетках вследствие устранения срывных зон.
Зная угол потока  и приведенную скорость
и приведенную скорость  на входе в решетку направляющего аппарата, и принимая угол на выходе из решетки
на входе в решетку направляющего аппарата, и принимая угол на выходе из решетки  , можно, используя график (рис. 5.4), определить оптимальное соотношение
, можно, используя график (рис. 5.4), определить оптимальное соотношение
 ,
,
где  - поворот потока в решетке первого ряда;
- поворот потока в решетке первого ряда;
 - потребный угол поворота потока в Н.А.
- потребный угол поворота потока в Н.А.
 |
 от преведенной скорости
от преведенной скорости  в решетках двухрядного направляющего аппарата
в решетках двухрядного направляющего аппарата
Тогда угол поворота потока в решетке первого ряда 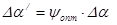 , а угол поворота потока в решетке второго ряда
, а угол поворота потока в решетке второго ряда 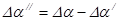 .
.
Полное давление потока за первым рядом определяется
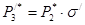 ,
,
где  - коэффициент восстановления полного давления в решетке первого ряда;
- коэффициент восстановления полного давления в решетке первого ряда;
 - коэффициент восстановления полного давления в Н.А.
- коэффициент восстановления полного давления в Н.А.
Приведенный расход за первым рядом лопатки
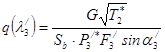 .
.
По таблицам ГДФ определяется  .
.
Выполненные экспериментальные исследования дают следующие соотношения геометрических размеров во взаимном расположении решеток первого и второго рядов (см. рис.5.5)
 |

 .
.
Дальнейшие детальные расчеты таких ступеней проводятся аналогично тому, что представлено выше в данной работе.
Дата добавления: 2015-10-29; просмотров: 289 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Особенности расчета закрутки сверхзвуковых (трансзвуковых) лопаток и лопаток с переменной работой по высоте | | | Расчет координат профиля |