
Читайте также:
|
Азғындылған Бозон газдары үшін үлестіру функциясы. Азғындылған Бозон газдары үшін үлестіру функциясы-әсерлесулері әлсіз және оны ескермеуге болатын нөлдік және бүтін спиндері бар бөлшектердің энергияларының теңдігімен анықталады. Демек, кванттық идеал газдың үлестірілуі Бозе- Эйнштейн үлестіруіне бағынады.Статистикалық теңдік жағдайында -бөлшектері былай анықталады [8].
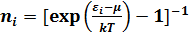 (1.4)
(1.4)
Мұндағы, i = бөлшектердің күйін сипаттайтын кванттық сандар жиынтығы, μ- химиялық потенциал.
1.2 Қатты денелер арасындағы байланыс
Қатты денелердің пайда болуы, олардың құрылымдық бөлшектерінің өте кішкентай ара қашықтыққа дейін жақындағанда пайда болатын әсерлесулерге негізделген. Қатты денеде нақты құрылым пайда болуы үшін екі түрлі күш әсер етуі қажет. Олар, бөлшектерді бір- бірінен алшақтанудан сақтайтын тартылыс күштері және бөлшектердің жақындауына кедергі жасайтын тебілу күштері. Келесі кезекте біз мынадай химиялық байланыстарды шарттандыратын тартылыс күшіне тоқталайық [10].
1. Бөлшектер арасындағы ең әмбебап байланыс- Ван-дер-Ваальсты байланыс. Энергиясы ̴ 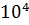 Дж/моль-ға тең әлсіз байланыс болып табылады. Таза күйде ол, бейтарап атомдар мен молекулалар өзара байланысы кезінде пайда болады. Жеке жағдайда Ван-дер-Ваальсты байланыс инертті газдардың (сутегі, оттегі, азот және т.б көптеген органикалық және бейорганикалық байланыстар) қатты және сұйық күйде кездесуін қамтамасыз етеді. Ван-дер-Ваальсты байланыстың энергиясы төмен болғандықтан, олар тұрақсыз және балқу темперетуралары төмен болады. Ван-дер-Ваальсты байланыс бөлшектер арасында, сонымен қатар молекулалар мен екі бөлшек арасында да бола береді.Бұл байланыс, нейтральды бөлшектер немесе атомдар тобы арасындағы дипольдік немесе дисперсиялық әсерлесуден пайда болатын байланыс [8].
Дж/моль-ға тең әлсіз байланыс болып табылады. Таза күйде ол, бейтарап атомдар мен молекулалар өзара байланысы кезінде пайда болады. Жеке жағдайда Ван-дер-Ваальсты байланыс инертті газдардың (сутегі, оттегі, азот және т.б көптеген органикалық және бейорганикалық байланыстар) қатты және сұйық күйде кездесуін қамтамасыз етеді. Ван-дер-Ваальсты байланыстың энергиясы төмен болғандықтан, олар тұрақсыз және балқу темперетуралары төмен болады. Ван-дер-Ваальсты байланыс бөлшектер арасында, сонымен қатар молекулалар мен екі бөлшек арасында да бола береді.Бұл байланыс, нейтральды бөлшектер немесе атомдар тобы арасындағы дипольдік немесе дисперсиялық әсерлесуден пайда болатын байланыс [8].
Ван-дер-Ваальсты байланыс үш әлсіз электромагниттік әсерлесуден тұрады:
Бағдарланған күштер, диполь-дипольді тартылу. Тұрақты диполь бола алатын молекулалар арасында болады. Мысал ретінде, HCl - дың сұйық және қатты күйде кездесуін келтіре аламыз. Мұндай байланыстың энергиясы дипольдердің ара қашықтығының кубына кері пропорцоинал.
Дисперсиялық тартылу- дәлденген және лездік дипольдің арасындағы әсерлесу. Мұндай байланыстың энергиясы дипольдердің ара қашықтығының алты дәрежесіне кері пропорцоинал.
Индукциялық тартылу, тұрақты және дәлденген (индукцияланған) дипольдар арасындағы әсерлесу. Мұндай байланыстың энергиясы дипольдердің ара қашықтығының алты дәрежесіне кері пропорцоинал.
Ионды байланыс неорганикалық байланыстар арасындағы кең таралған байланыс түрі. Бұл, металлдар мен металл еместер арасындағы байланыс. Байланыс түріне, металлдардың галоидтармен, металл оксидтерімен, сульфидтері және т.б полярлы байланыстар жатады. Осының әсерінен металлдардың электрондары металл еместерге барып, ион түзеді. Ионды байланыстың энергиясы Ван-дер-Ваальсты байланыс энергиясынан әлдеқайда жоғары, сандық мәні жағынан  Дж/моль- ға тең. Сондықтан, иондық байланысы бар қатты денелер сублимацияның және балқу температурасының жоғарғы болуын қамтамасыз етеді [10].
Дж/моль- ға тең. Сондықтан, иондық байланысы бар қатты денелер сублимацияның және балқу температурасының жоғарғы болуын қамтамасыз етеді [10].
Иондық байланыс, бұл атомдар арасындағы үлкен теріс заряд (>1,5 Полинги шкаласы бойынша) тудыратын химиялық байланыс. Мұның әсерінен электронды жұптар көп жағдайда заряды теріс атомға көшеді. Басқаша айтқанда, бұл зарядталған денелердің байланысы. Мысал ретінде CsF алсақ болады, оның иондық байланысы 97% тең. Иондық байланыс ковалентті полярлы байланыстың соңғы нәтижесі: A ̇ +  [:
[:  ]
]
Пайда болған иондар арасында иондық байланыс пайда болады. Бұл байланыстың басқаларға қарағандағы ерекшелігі, олардың қанықпағандылығы мен бағытталмағандығы. Байланыстың негізгі сипаттамасы полярлы ерітінділерде (су, қышқылдар, т.б) жақсы ерігіштік қасиеті болып табылады. Бұл зарядталған молекула бөлшектерінің әсерінен болады. Осы кезде, ерітіндінің дипольдері молекуланың зарядталған бөлщектеріне тартылып, Броундық қозғалыс нәтижесінде денедегі бөлшектерге қайта бірікпеуін қамтамасыз етеді. Нәтижесінде, ерітіндіні айнала қоршаған дипольдер пайда болады [11].
Ионды байланыстың пайда болуы. Мысал ретінде NaCl натрий хлоридін қарастырайық. Электронды конфигурациясы  және
және  . Бұл атомдардың энергетикалық деңгейінің сыртқы қабаты толмаған. Бұл жағдайда, натрий атомына 7 электрон қосып алғанша, 1 элетрон берген ыңғайлы, ал хлор атомына 7 электрон бергенше 1 электрон қосып алған ыңғайлы. Химиялық әсерлесу нәтижесінде, натрий 1 атомын беріп, ал хлор оны қосып алады. Схематикалық түрде оны былай бейнелейміз:
. Бұл атомдардың энергетикалық деңгейінің сыртқы қабаты толмаған. Бұл жағдайда, натрий атомына 7 электрон қосып алғанша, 1 элетрон берген ыңғайлы, ал хлор атомына 7 электрон бергенше 1 электрон қосып алған ыңғайлы. Химиялық әсерлесу нәтижесінде, натрий 1 атомын беріп, ал хлор оны қосып алады. Схематикалық түрде оны былай бейнелейміз:
Na - e  , натрий ионы 8 электроннан тұратын мықты ион және Cl + e
, натрий ионы 8 электроннан тұратын мықты ион және Cl + e 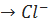 иондары.
иондары.  және
және  иондары арасында электростатикалық тартылыс күші болып, нәтижесінде иондық байланыс пайда болады.
иондары арасында электростатикалық тартылыс күші болып, нәтижесінде иондық байланыс пайда болады.
Ковалентті байланыс. Кейбір металдар мен интерметалдық байланыстар, органикалық байланыстар арасында болатын кең таралған байланыс түрі. Бұл байланыс алмаз, германий, т.б тәрізді валентті кристалдардың пайда болуына негізделген. Ковалентті байланыстың энергиясы 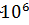 Дж/моль, ол сублимация мен балқу температурасының жоғары болғандығын көрсетеді. Ковалентті байланыстың қасиеттері: бағыттылық, қанығу, полярлығы және полярлануы байланыстың физикалық және химиялық қасиеттерін сипаттайды. Байланыстың бағыттылығы, молекулалардың геометриялық формалары мен құрылымына негізделген. Екі байланыстың арасындағы бұрыш валенттілік деп аталады [12].
Дж/моль, ол сублимация мен балқу температурасының жоғары болғандығын көрсетеді. Ковалентті байланыстың қасиеттері: бағыттылық, қанығу, полярлығы және полярлануы байланыстың физикалық және химиялық қасиеттерін сипаттайды. Байланыстың бағыттылығы, молекулалардың геометриялық формалары мен құрылымына негізделген. Екі байланыстың арасындағы бұрыш валенттілік деп аталады [12].
Қанықтылық, шектелген ковалентті байланыстарды түзу мүмкіндігі. Атомдар түзетін байланыстардың саны атомдардың сыртқы атомдық орбитальдарымен шектелген. Байланыстың полярлығы электронды тығыздықтың атомның теріс зарядтылығына байланысты бірқалыпты таралмағандығына негізделген. Осы құбылысқа байланысты ковалентті байланысты полярлы және полярлы емес деп екі топқа ажыратады. Полярлы ковалентті байланыс дегеніміз, әр түрлі химиялық элементтің атомынан тұратын екі атомды молекула. Мұндағы, электронды бұлт атомның бір жағына қарай молекулада асимметриялық таралып, молекуланың дипольді моментін туғызады. Полярлы емес ковалентті байланыс, бірдей атомнан (H2, Cl2, N2) тұратын екі атомды молекула. Әр атомға электронды бұлт симметриялы таралған. Байланыстың полярлануы сыртқы электр өрістің және басқа да бөлшектің әсерінен электронды байланыстардың ығысуына негізделген. Полярлану электрондардың қозғалғыштығымен анықталады. Ковалентті байланыстың полярлығы және полярлануы, полярлы реагенттерге байланысты молекулалардың реакцияға қатысу мүмкіндігін анықтайды. Электрондардың қозғалғыштығы неғұрлым жоғары болса, соғұрлым олар ядродан алыс орналасады [13].
Байланыстың пайда болуы: Ковалентті байланыс екі атом арасында бөлінген электрон жұбынан пайда болады. Бұл электрондар әр атом есебінен екі орбитальға ие болуы керек: A· + ·В → А: В
Электрондардың бірігуі нәтижесінде толған энергетикалық деңгей пайда болады. Егер, олардың толық энергиясы алғашқы күйдегі энергиясынан аз болса ғана байланыс пайда болады.
Ковалентті байланыстың түрлері: Пайда болу механизміне қарай ковалентті байланысты 3 түрге бөледі [14]. Олар:
1. Қарапайым ковалентті байланыс. Бұл байланыстың пайда болуына әрбір атом жұпталмаған бір электрон беруі керек. Байланыс кезінде атом зарядтары өзгермейді. Егер, қарапайым ковалентті баланыс түзетін атомдар бірдей болса, молекула ішіндегі атом зарядтары да бірдей болады. Себебі, байланыс түзетін атомдар бірдей жағдайда ортақ электрондық жұпқа ие болады. Мұндай байланыс полярлы емес ковалентті байланыс деп аталады. Бұл байланысқа жай заттар ие болады. Мысалы, О2,N2, Cl2, т.б.
Егер атомдар әртүрлі болса, онда ортақ электрондар жұбы атомдардың теріс электр зрядтарымен анықталады. Теріс электр заряды үлкен атомдар өзіне қарай электрондық жұптарды тез тартады, осының нәтижесінде атомның заряды теріс болады. Теріс электр заряды аз атом сәйкесінше оң зарядқа ие болады. Егер, байланыс екі әртүрлі металл еместермен болатын болса, мұндай байланыс полярлы ковалентті байланы деп аталады [15].
2. Донорлы- акцепторлы байланыс. Бұл байланысты алу үшін атомдардың біреуі донор болуы қажет. Байланыс түзетін екінші бір атом акцептор деп аталады. Пайда болған молекулада донорда заряд бірге артық, ал акцепторда бірге кем болады.
3. Жартылай полярлы байланыс. Бұл байланыс түрін полярлы донорлы- акцепторлы байланыс ретінде қарастырса болады.Бұл ковалентті байланыстың түрін электрондық жұптары бөлінбеген атомдар (азот, фосфор, күміс, дер және т.б) арасында пайда болады. Жартылай полярлы байланыстың пайда болы екі этаптан өтеді:
- Ажыратылмаған электрондық жұптан жұпталмаған электрондық жұпқа 1 атомды көшіру. Нәтижесінде, ажыратылмаған жұп электрондары катион- радикалдарына айналады (оң зарядталған жұпталмаған электрон), ал екі жұпталмаған электрондар- анион- радикалдарына айналады (теріс зарядталған жұпталмаған электрон).
- Жұпталмаған электрондардың ортақтылығы (қарапайым ковалентті байланыс сияқты).
Ковалентті байланысқа мысалдар. Мысал ретінде біз қарапайым газ (Н2, Cl2 және т.б) молекулаларының атомдарын және қосылыстарын (Н2О, NH3, CH4, СО2, HCl және т.б) жатқыза аламыз. Донорлы- акцепторлы байланыс ретінде - аммоний NH4+, тетрафторборат анионы BF4−, т.б. Жартылай полярлы байланысқа, азоттың тотықтары N2O, O−-PCl3+. Ковалентті байланысы бар кристаллдарға диэлектриктер мен жартылай өткізгіштерді жатқызамыз. Қарапайым мысал ретінде алмаз, германий, кремний, т.б айтуға болады.
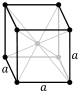
4. Металлды байланыс. Интерметалды және металды байланыстардың кристалдық торларындағы электрондардың ортақтасуының нәтижесінде пайда болатын байланыс. Байланыс энергиясы 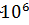 Дж/моль- ға тең. Металлдың кристаллдық торының түйіндерінде оң иондар орналасқан. Олардың арасында ретсіз, молекулалық газ тәрізді электрондар қозғалыста болады. Бұл электрондар металл атомдарынан ион пайда болған кезде болады. Сонымен қатар бұл электрондар, оң иондарды бірге ұстап тұратын цемент рөлін атқарады. Егер, мұндай жағдай болмаса иондар арасындағы итеру күштері әсерінен кристалдық тор жойылатын еді. Осы себептен, иондар электрондарды кристалдық тордың ішінде шығармай ұстап отырады. Байланыс күштері ауыздықталмаған және бағытталмаған. Металдарда көп жағдайда жоғарғы координациялық сандар кездеседі. Осылайша, сілтілік металдар көлемдік- орталықтанған кубтық торда кристаллизацияланады және әрбір металдың оң зарядталған сілтілік ионы жақын орналасқан 8 көрші ионнан (оң зарядталған) тұрады (3 сурет).
Дж/моль- ға тең. Металлдың кристаллдық торының түйіндерінде оң иондар орналасқан. Олардың арасында ретсіз, молекулалық газ тәрізді электрондар қозғалыста болады. Бұл электрондар металл атомдарынан ион пайда болған кезде болады. Сонымен қатар бұл электрондар, оң иондарды бірге ұстап тұратын цемент рөлін атқарады. Егер, мұндай жағдай болмаса иондар арасындағы итеру күштері әсерінен кристалдық тор жойылатын еді. Осы себептен, иондар электрондарды кристалдық тордың ішінде шығармай ұстап отырады. Байланыс күштері ауыздықталмаған және бағытталмаған. Металдарда көп жағдайда жоғарғы координациялық сандар кездеседі. Осылайша, сілтілік металдар көлемдік- орталықтанған кубтық торда кристаллизацияланады және әрбір металдың оң зарядталған сілтілік ионы жақын орналасқан 8 көрші ионнан (оң зарядталған) тұрады (3 сурет).
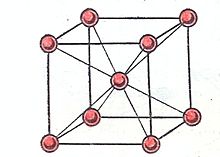
3 сурет. Сілтілік металл кристаллында иондардың орналасуы [16]
Аттас зарядталған бөлшектердің кулондық итеру күштері нысандарды байланыстыратын электрондардың электростатикалық тартылуын теңелтеді. Олардың пішіні, биіктігі сілтілік металдың бүйір жағының базисі тұрақты a w кристалдық торына тең квадрат бипирамидаға сәйкес келеді. Байланыстыратын электрондар сілтілік металл ішіндегі алты оң ионнан тұратын жүйеде ортақ болады және соңғысын кулондық итеру күшінен ұстап тұрады. Сілтілік металл кристалындағы тұрақты трансляциялық тордың a w мөлшері сілітілік металл ішіндегі коваленттік байланыстың мөлшерінен әлдеқайда жоғары болады. Сол себепті, электрондар металл ішінде еркін қозғалыста болады деп қарастырылады [17].
Кристаллдық торлардың сипаттары. Металдарың көпшілігі симметриялық торлардың келесі түрін құрайды: кубты көлемдік орталықтанған, кубты шекті орталықтанған және гексогональды. Кубты көлемдік орталықтанған торда атомдар кубтың жоғарғы жағында және бір атом көлемдік кубтың ортасында орналасқан. Осындай торға ие металдардың қатарына, Pb, K, Na, Li, β-Ti, β-Zr, Ta, W, V, α-Fe, Cr,Nb, Ba, т.б жатқызуға болады. Ал кубты шекті орталықтанған кристалды торда атомдар кубтың төбесінде және шектің ортасында орналасқан. Бұл кристалдық торға мыналарды жатқызамыз: α-Ca, Ce, α-Sr, Pb, Ni, Ag, Au, Pd, Pt, Rh, γ-Fe, Cu, α-Co және т.б.
Ал гексогональды торға алты қырлы призма негізінде жоғарыда және орталықта орналасқан атомдар, ал 3 атом призманың орталық жазықтығында орналасқан. Мұндай кристалдық торға Mg, α-Ti, Cd, Re, Os, Ru, Zn, β-Co, Be және т.б жатады.
Басқада қасиеттері. Еркін қозғалыстағы электрондар жоғары электр және жылу өткізгіштікті қамтамасыз етеді. Көптеген металлдар аса қаттылыққа ие. Мысалы, хром, молибден, тантал, вольфрам, т.б. Металлдық байланысқа ие заттардың барлығы пластикалық беріктілікке ие. Себебі, атомдар орын ауыстырғанда металлдық байланыс үзілмейді.
Сутекті байланыс. Бұл байланыс түрі, сутегі атомы келесі бір теріс зарядталған атоммен байланысқа түскенде пайда болады. Мысалы, оттегі, фтор, азот, хлор және т.б атомдар. Бұл байланыс түрі әлсіз болғанымен, табиғатта өте маңызда рөл атқарады. Сутекті байланыс молекулааралық және молекулаішілік болуы мүмкін [18].
Қасиеттері. Сутекті байланыстың энергиясы ковалентті байланысқа қарағанда әлдеқайда аз болады, 40 кДж/моль- дан аспайды [19]. Алайда бұл энергия молекулаларды біріктіруге жеткілікті, яғни димерлер мен полимерлерді біріктіруге. Молекулалардың бірігуі балқу және қайнау темперетурасының аномальды өсуіне себепші. Мысалы, фторсутек, су, аммиак. Бұл байланыстың түрі ионды және ковалентті байланыстан әлсіз болсада, молекула аралық және ішілік байланысуларда маңызды орын алады. Сутекті байланыс көп жағдайда судың және көптеген органикалық сұйықтардың (спирт, корбон қышқылы, карбон қышқылдарының амиды, эфирлер) физикалық қасиетін сипаттайды. Сутекті байланыстың мықтылығы полярлы комплекске байланысты және
~ 6 кДж/моль тербеледі.
1.3 Кристаллды торлар
Кристалдарда сипаттаған кезде кристалдық тор ұғымына сүйенеміз. Олар кеңістіктік тор сияқты атомдар мен молекулалардан және иондардан құралады. Олар осылай кристалдық тор түзеді. Геометриялық жағынан қарағанда, бөлшектердің кристалда периодты түрде орналасуын параллель көшіру немесе трансляция көмегімен жасауға болады [7]. Мысалы, 3 өс бойымен трансляция көмегімен мынадай тор алуға болады:
ox –кесіндісінде, 2a, 3a, … ma;
oy – кесіндісінде, 2b, 3b, … nb;
oz – кесіндісінде, 2c, 3c, … pc.
Кез келген бөлшектің осындай торда орналасуын мына вектормен анықтаса болады.
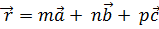 . (1.5)
. (1.5)
Мұндағы, 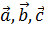 трансляция векторлары, ал олардың сандық мәні трансляция периодтары деп аталады. Қандай да бір үш бағытпен трансляция арқылы құрылған тор Бравэ кристаллдық торы деп аталады.Үш өлшемді торларда Браве ұяшығы шекті орталықтанған, көлемді орталықтанған, примитивті, ромбоэдрлік болып кездеседі. Примитивті трансляция жүйесі көптеген
трансляция векторлары, ал олардың сандық мәні трансляция периодтары деп аталады. Қандай да бір үш бағытпен трансляция арқылы құрылған тор Бравэ кристаллдық торы деп аталады.Үш өлшемді торларда Браве ұяшығы шекті орталықтанған, көлемді орталықтанған, примитивті, ромбоэдрлік болып кездеседі. Примитивті трансляция жүйесі көптеген 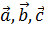 векторларынан тұрады, ал қалғандары бірнеше қосымша трансляциялардан тұрады (4 сурет).
векторларынан тұрады, ал қалғандары бірнеше қосымша трансляциялардан тұрады (4 сурет).

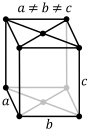

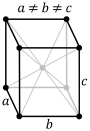
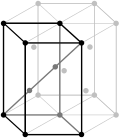 Примитивті Базоцентрленген Шекті Көлемді Ромбоэдрлік
Примитивті Базоцентрленген Шекті Көлемді Ромбоэдрлік
орталықтанған орталықтанған
4 сурет. Браве ұяшықтарының түрлері [20].
Сонымен, көлемді орталықтанған Браве трансляциясында 4 вектор (a, b, c, ½(a + b + c)), ал шекті орталықтанғанға алты (a, b, c, ½(a + b), ½(b + c), ½(a + c)) вектор кіреді. Ал базо орталықтанған трансляция жүйесіне 4 вектордан сәйкес келеді (a, b, c,½(b + c)), B - векторы (a, b, c, ½(a + c)), ал C - (a, b, c, ½(a + b)).
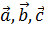 векторларынан құралған ең кіші параллелепипед элементар ұяшық деп аталады. Бұл дегеніміз, кристалдардың көп реттік қайталану арқылы параллелепипед құруға болатындығын анықтайды. Біртекті атомдардың ара қашықтығын периад немесе кристалдық тордың тұрақтысы деп атайды. Торды құратын барлық элементар ұяшықтар көлемдері және пішіндері жағынан бірдей болады. Ұяшықтың төбелерінде бірдей атомдар немесе атомдық топтар орналасқан. Осы себепті, ұяшықтың барлық төбелері бір- біріне эквивалентті болады. Оларды тор түйіндері деп атайды [21]. Элементар ұяшықты сипаттау үшін 6 шама қажет, олар: ұяшықтың 3 жағы a,b,c және олардың арасындағы бұрыш α, β, γ.
векторларынан құралған ең кіші параллелепипед элементар ұяшық деп аталады. Бұл дегеніміз, кристалдардың көп реттік қайталану арқылы параллелепипед құруға болатындығын анықтайды. Біртекті атомдардың ара қашықтығын периад немесе кристалдық тордың тұрақтысы деп атайды. Торды құратын барлық элементар ұяшықтар көлемдері және пішіндері жағынан бірдей болады. Ұяшықтың төбелерінде бірдей атомдар немесе атомдық топтар орналасқан. Осы себепті, ұяшықтың барлық төбелері бір- біріне эквивалентті болады. Оларды тор түйіндері деп атайды [21]. Элементар ұяшықты сипаттау үшін 6 шама қажет, олар: ұяшықтың 3 жағы a,b,c және олардың арасындағы бұрыш α, β, γ.
V= abc 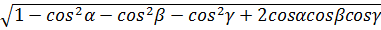 (1.6)
(1.6)
Ұяшықтың көлемі (1.6) формуламен анықталады.
Бұл шамалар элементар ұяшықтың параметрлері деп аталады.
Жазықтықтың симметриясына байланысты барлық кристалдық торлар 6 кристалдық жүйеге бөлінеді. Элементар ұяшықтың пішініне қарай олар 6 сингонияға бірігеді. Айналмалы өс симметриясы мен жазықтықтық симметрия кристалдық торларды 32 симметрия кластарына бөледі, ал бұрандалық өс симметриясы 230 жазықтықтық топқа бөледі [22].
Симметрия бойынша торлардың классификациясы (1 кесте).
Сингониялар:
Төменгі деңгей (трансляциялары бір- біріне тең емес)
-Триклинді: 
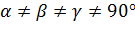 ,
,
-Моноклинді: 
 ,
, 
-Ромбылы: 

Орташа деңгей (3 трансляцияның ішінен 2- уі тең)
-Тетрагональды: a=b 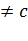 ,
, 
-Гексагональды: a=b 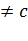 ,
, 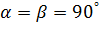 ,
, 
Жоғарғы деңгей (трансляциялары өзара тең)
-кубтық: a=b=c, α=β=γ=90.
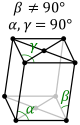
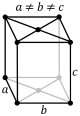
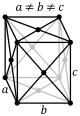
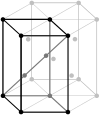
1 кесте. Сингониялар [23]
| Сингония | Браве ұяшығының орталықтануы | ||||
| Прими-тивті | базо- центрленген | Көлемді центрленген | Шекті центрленген | ромбылы | |
| Триклинді (параллелепипед) | 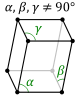
| ||||
| Моноклинді (параллелограммом негізді призма) | 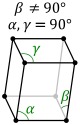
| 
| |||
| Ромбылы (тік бұрышты параллелепипед) | 
| 
| 
| 
| |
| Тетрогональды (квадрат негізді тікбұрышты параллелепипед) | 
| 
| |||
| Гексагональді (алты бұрышты дұрыс орталықтанған призма) | 
| 
| |||
| Кубты (куб) | 
| 
| 
|
1.4 Атомдық жазықтық
Кристаллографиялық бағыт және жазықтық. Жазықтықтық торда кристалдық құрылымның реттеліп орналасуы кристаллографиялық бағыттар мен жазықтықтарды анықтауға мүмкіндік береді [24].
Кристаллографиялық бағыт - кристалдық торға жанама орналасқан атомдардың санақ нүктесінен шығатын сипаттық түзу сызықтар болып табылады. Санақ нүктесі болып кубтың төбесі, ал кристаллографиялық бағыты болып оның диагоналі мен қабырғалары және шектік диагональдар болуы мүмкін.
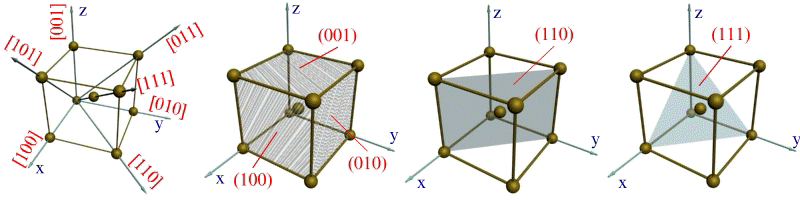
а) б) в) г)
а)- негізгі бағыттары мен белгіленуі, б), в), г)- негізгі жазықтықтар мен олардың белгіленуі
5 сурет. Кристалдық тордағы кристаллографиялық бағыттар мен жазықтықтары [15]
Кристаллографиялық жазықтықты сипаттауда Миллер индекстері маңызды орын алады. Бұл индекстерді қалай анықтаймыз? Миллер индекстері дегеніміз,
кристалдық торда атомдық жазықтықтардың орналасуын сипаттайтын кристаллографиялық индекстер. Бұл индекстер қималар және кристаллографиялық жүйе координаттарында 3 жазықтықтан таңдап алынған жазықтықты қиятынмен байланысты (міндетті түрде Декарттық координата емес). Осындай жолмен өстер мен жазықтықтың орналасуының 3 түрлі жолы бар [25]:
- жазықтық 3 өсті де қияды;
- жазықтық 2 өсті қияды, ал 3-шісі параллель;
- жазықтық 1 өсті қияды, ал қалған екеуіне параллель;
Миллер индекстері төмендегідей белгіленеді: (111), (101), (110)… Кристаллографиялық бағыттар мен жазықтықтар, мысалы, шекті кубтың жазықтығы болып табылады, сонымен қатар, әр түрлі диагональдық жазықтықтар мен оларда орналасқан атомдар бар. Қандай да бір бағыттың индексін табу үшін, оған ең жақын орналасқан санақ нүктесінің индексін табу керек. Мысалы, 0Х өсіне ең жақын орналасқан индексті 100 санымен белгілейік. (а сурет) Бұл сандар 0 нүктесіне қатысты координаттарды анықтайды. Сәйкесінше, бұл координаттар ОХ, ОУ, ОZ өстерінің параметрлеріне сәйкес келеді. ОХ және оған параллель бағыттағы индекстерді [100] деп белгілейік. Сәйкесінше,бағыттары да ОУ, ОZ өсімен [010] және [001] тең болады. Кристаллографиялық бағыттар шек диагональдарына XOZ, XOY және YOZ мынадай [101], [110] және [011] деп белгілейік. Осы әдісті пайдалана отырып, кез келген бағыттың индекстерін анықтауға болады [26].
Мысалы, кубқа жанама бағыттағы индексті былай белгілесе болады: [111]. Кристаллографиялық жазықтықтың индекстерін табу үшін, ең алдымен санақ 0 нүктесінен координат өсіне ең жақын орналасқан нүктелердің қимасын табу керек. Сосын, оларға кері мәндерін алып дөңгелек жақшада ретпен жазу керек.
Мысалы, XOY параллель жазықтығына жақын орналасқан жазықтықтың координаттық қиылысу нүктелерін аламыз. Олар, 001 сандары.Сондықтан да, бұл жазықтықтың индекстерін былай жазуға болады (001). Жазықтықтың индекстері, параллель жазықтықтарда XOZ и YOZ былай жазылады: (010) и (100). (б сурет). Ал кубтың тік диагональ жазықтығын осылайша өрнектеуге болады: (110), ал көлбеу жазықтықтарда (111), (г сурет).
1.5 Кері торлар
Мұнда арақашықтық ұзындықтың кері өлшемділігіне ие бола алатын абстракты кері кеңістіктегі нүктелік үш өлшемді тор. Кері тор ұғымын рентгенді сәулелердің, нейтрондардың және электрондардың дифракциясын сипаттағанда қажетті ұғымдардың бірі болып табылады. Әрбір кристалды құрылымға екі тор сәйкес келеді: кристалды тор және кері тор. 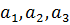 тура және
тура және  кері торлардың векторларын анықтауға болады. Кристалды тор, бұл қарапайым кеңістіктегі тор, ал кері тор- Фурье кеңістігіндегі торлар. Кристаллографияда кері тор көптеген К векторлардан тұрады.
кері торлардың векторларын анықтауға болады. Кристалды тор, бұл қарапайым кеңістіктегі тор, ал кері тор- Фурье кеңістігіндегі торлар. Кристаллографияда кері тор көптеген К векторлардан тұрады. 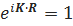 . Әрбір R векторы кристалды торда түйіндердің орналасуын көрсетеді. Базисті векторлармен сипатталатын (
. Әрбір R векторы кристалды торда түйіндердің орналасуын көрсетеді. Базисті векторлармен сипатталатын (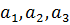 )шексіз үш өлшемді тор үшін, оның кері торы үштік базистік векторлар (
)шексіз үш өлшемді тор үшін, оның кері торы үштік базистік векторлар ( )арқылы өрнектеледі [7]. Оның тура тормен байланысы
)арқылы өрнектеледі [7]. Оның тура тормен байланысы
 , j=k; 0, j
, j=k; 0, j  (1.7)
(1.7)
М формуламен анықталады:

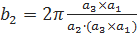 (1.8)
(1.8)

Жоғарыда анықталған формула физикалық анықтама деп аталады. Себебі, Мұндағы 2π көбейткіші периодтық құрылымды анықтағанда пайда болады. Кристаллография анықтамасының эквиваленттілігі, кері тор мына қатынасқа бағынатын болса орындалады. 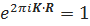 .
.
Бұл формула кері тор векторларын былай анықтайды:

Мұнда, кристаллография анықтамасы арқылы 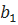 кері өлшемін
кері өлшемін  өлшемі арқылы
өлшемі арқылы  бағытта, яғни 2π көбейткішінсіз анықтауға болады.
бағытта, яғни 2π көбейткішінсіз анықтауға болады.
Кері тор кеңістік индекстерін анықтауда қолданылады. Кез келген кристаллографиялық жазықтықта кері торды қысқа бірлік вектор коэффициенттерімен анықтаса болады. Кері тордың параметрлері мен элементар ауыстыру векторлары арасында белгілі бір байланыс бар. Мысал ретінде, кристалды тордың элементар ұяшығында 3 элементар ауыстыру бар деп қарастырайық  (суретте). Координат жазықтықтары ең қарапайым жазықтықтың торлары болып табылады.
(суретте). Координат жазықтықтары ең қарапайым жазықтықтың торлары болып табылады.  және
және 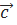 параллель векторларының жазықтықтар кеңістігі (100),. Оны басқаша
параллель векторларының жазықтықтар кеңістігі (100),. Оны басқаша  векторының осы жазықтыққа перпендикуляр соңғы нүктесі ретінде белгілеуге болады. Осы вектордың ұзындығы ретінде, жазықтықаралық арақашықтықтың кері мәнін алса болады:
векторының осы жазықтыққа перпендикуляр соңғы нүктесі ретінде белгілеуге болады. Осы вектордың ұзындығы ретінде, жазықтықаралық арақашықтықтың кері мәнін алса болады:  =|0
=|0  | Мұндағы, | 0
| Мұндағы, | 0  | - (100) жазықтығының нормаліне
| - (100) жазықтығының нормаліне  векторының проекциясы.
векторының проекциясы.  векторының ұзындығын мынадай шарттармен анықтаса болады:
векторының ұзындығын мынадай шарттармен анықтаса болады: 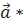 | 0
| 0  | =1 [27].
| =1 [27].
Сонымен қатар,  векторы жазықтық нормаліне жанама орналастырылады. Себебі,
векторы жазықтық нормаліне жанама орналастырылады. Себебі, 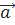 векторының бағытына жанама қараған бақылаушы
векторының бағытына жанама қараған бақылаушы  және векторларының қозғалысы сағат тіліне бағыттас екенін көрсе болады (6 сурет).
және векторларының қозғалысы сағат тіліне бағыттас екенін көрсе болады (6 сурет).
Векторлық шартта олар былай жазылады:
( )=1, (
)=1, ( )=0, (
)=0, (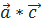 )=0 (1.9)
)=0 (1.9)
Ал қалған  және
және 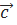 векторларын басқа координаттық жазықтықта анықтайды:
векторларын басқа координаттық жазықтықта анықтайды:
(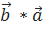 )=0, (
)=0, ( )=1, (
)=1, ( )=0
)=0
(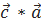 )=0, (
)=0, ( )=0, (
)=0, (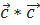 )=1 (1.10)
)=1 (1.10)
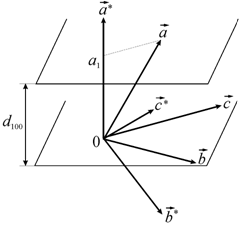
6 сурет. Тура және кері торлардың параметрлері арасындағы байланыс [28]
Кері кеңістіктің координат басы болатын кез келген 

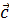 , векторларын жүргіземіз. Осы векторлар арқылы тура кристалға кері тор болатын нүктелік тор құрылады. Тура тордың элементар ұяшығының көлемі V, онда
, векторларын жүргіземіз. Осы векторлар арқылы тура кристалға кері тор болатын нүктелік тор құрылады. Тура тордың элементар ұяшығының көлемі V, онда
| 0  |=
|=  =
= 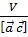 (1.11)
(1.11)
Осыдан,
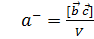 (1.12)
(1.12)


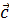 , векторлары арасындағы бұрыштарды
, векторлары арасындағы бұрыштарды  ,
,  деп белгілейік. Олардың шамасы бойынша триэдрдің екіжақты бұрышына тең:
деп белгілейік. Олардың шамасы бойынша триэдрдің екіжақты бұрышына тең:
cos  =
= 
cos 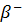 =
= 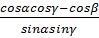 (1.13)
(1.13)
cos  =
= 
Егер кристалды тордың барлық бұрыштары тік болса, олардың элементар трансляциялары 

 , кері торға векторлары параллель және шамасы жағынан кері болады Бұл қорытындыға (1.5) формула арқылы келе аламыз. Шын мәнінде де, бұл жағдайда элементар ұяшықтың көлемі V=abc, ал векторлық көбейтіндісі [
, кері торға векторлары параллель және шамасы жағынан кері болады Бұл қорытындыға (1.5) формула арқылы келе аламыз. Шын мәнінде де, бұл жағдайда элементар ұяшықтың көлемі V=abc, ал векторлық көбейтіндісі [  ]=bc болады. Сондықтан,
]=bc болады. Сондықтан, 
Кері тордың элементар ұяшығының көлемі төмендегіге тең:
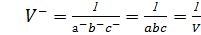 (1.14)
(1.14)
Мұндағы,
V  =1 (1.15)
=1 (1.15)
Осылайша, кері тордың элементар ұяшығының көлемі 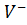 , кристал тордың элементар ұяшығына кері шама болып табылады. Бұл қатынас барлық кристалл торларға қолданылады. Кері тордың кез келген векторы
, кристал тордың элементар ұяшығына кері шама болып табылады. Бұл қатынас барлық кристалл торларға қолданылады. Кері тордың кез келген векторы 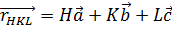 тік кристалл тордың жазықтығына (HKL) перпендикуляр, ал ұзындығы кері жазықтықаралық шамаға тең [29]:
тік кристалл тордың жазықтығына (HKL) перпендикуляр, ал ұзындығы кері жазықтықаралық шамаға тең [29]:
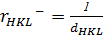 (1.16)
(1.16)
Сонымен, кері және тік ұяшыұтар бір- бірімен өзара байланысты. [[ HKL ]]* кері торының әрбір түйіні тік түйіннің (HKL) параллель жазықтықтарына сәйкес келеді. Кері тор, өзі Бравэ ұяшығы болып табылады.
2 НЕЙТРОНДЫ ЖҰЛДЫЗДАР ЖӘНЕ АҚ ЕРГЕЖЕЙЛІЛЕР
2.1 Компактті жұлдыздар
Компактты жұлдыздар - нейтронды жұлдыздар, ақ ергежейлілер, қара құрдымдар - нормаль жұлдыздардан кейін пайда болады, бұл дегеніміз, жанып тұрған ядролы жұлдыздың көп бөлігі жойылған кезде. Біздің галактикада миллиардтан астам ақ ергежейлілер, жүз миллиондаған нейтронды жұлдыздар және бірнеше жүз қара құрдымдар бар. Компактты женелерді зерттеу ең алдымен ақ ергежейлілерден басталды [30]. Оның құрылымын Ферми-Дирак статистикасымен анықтады және гравитациялық коллапстан оларды азғындалған электронды газдың қысымы ұстап тұрады. Бұл идеяны алғаш рет 1926 жылы Фаулер айтты. Уақыт өткен сайын аспанда жаңа жұлдыздар пайда болатындығы астрономдарға белгілі, бірақ мұндай жарқыраулар өте жиі болады. Жыл сайын жұлдыздар жүйесі - Галактикада астрономиялық бақылауға болатын ондаған жұлдыз пайда болады.Мысалы, 1885- 1920 жылдары әр түрлі галактикаларда 10 осындай тұтану пайда болды. Бұл тұтанулар галактиканың әр түрлі формаларымен (эллипстік, спиральды) бақыланды. Мұндай құбылыстар жүз жылда біп рет қана болады. 1934 жылы америкалық ғалымдар Цвикки және Бадее бұлжұлдыздарды "компактты" деп атады. Компактты құбылыс деп қарастырылған бұл жұлдыздың жарылысы нәтижесінде, айналасында  10000км/с жылдамдықпен таралатын тұмандық пайда болады.
10000км/с жылдамдықпен таралатын тұмандық пайда болады.
Егер, жұлдыз неге жарылысқа ұшырайды деген сұраққа теориялық жауап іздесек, онда ол ядролық энергияға байланысты болады. Жанып тұрған ядролық сутегіні бітіргенде, орталық аудандарда жұлдыздың даму эволяциясы біршама өзгереді. Даму эволюциясының соңғы кезеңіндегі жұлдыздың тепе- теңдік күйі, барлық даму процесінде өзгеріссіз қалатын бастапқы массасына тәуелді болады. Жұлдыздың идеал моделі, өзінің массасын сақтайды және айналмайды. Осындай оңайлатылған шешімге қарап, біз жұлдыздың мүмкін болатын даму эволюциясының қатарын келтіре аламыз. Егер, идеал жұлдыздың массасы 1,2 Күндікінен кіші болса, дамудың соңғы нәтижесі ақ ергежейлі жұлдыз болады. Ал, егер, 1,2 Күннің массасынан көп және 2,5 кіші болса, онда азғындалған газдың құрылымы тепе- теңдікте болады. Бұл, 1938 жылы Оппенгеймер мен Волковтың шешімдері бойынша нейтронды жұлдыз болып табылады. Егер, жұлдыздың массасы, 2,5-ке жуық болса, онда олар бір нүктеге сығылуы қажет, басқаша бұл құбылысты қара құрдым деп атаймыз. Сонымен, компактты обьектілер дегеніміз, жұлдыздар дамуының соңғы кезеңі. Жұлдыз өмір сүруін нейтронды жұлдыз, ақ ергежейлі немесе қара құрдым болып тоқтама, ол оның бастапқы массасына байланысты болады (7 сурет).

7 сурет. Компактты объектілердің даму схемасы [31]
Компактты жұлдыздардың нормаль жұлдыздардан айырмашылықтары төмендегіей:
- термодинамикалық қысымнынң әсерінен жанып тұрған ядролы жұлдыз гравитациялық коллапсқа төтеп бере алмайды;
- өлшемдері;
-жарықтылығы.
Мысалы, ақ ергежейлілер массасы M 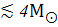 жеңіл жұлдыздардан пайда болады. Ал, нейтронды жұлдыздар мен қара құрдымдар массасы аса үлкен жұлдыздардан пайда болады. Нейтронды жұлдыздар үшін массасы 1,4-3
жеңіл жұлдыздардан пайда болады. Ал, нейтронды жұлдыздар мен қара құрдымдар массасы аса үлкен жұлдыздардан пайда болады. Нейтронды жұлдыздар үшін массасы 1,4-3  . Жұлдызды эволюцияның нәтижесінде массаға тәуелді жұлдыздардың нәтижесі анықталды (2 кесте).
. Жұлдызды эволюцияның нәтижесінде массаға тәуелді жұлдыздардың нәтижесі анықталды (2 кесте).
2 кесте. Массаға тәуелді жұлдызды эволюцияның нәтижесі [32]
| Масса диапазондары | Нәтижесі |

| Өмір сүру уақыты Әлемнің жасынан асады |
1≲ 
| Ақ ергежейлі+ планетарлы тұмандық |
(3  )≲ )≲ 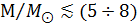
| Массаны жоғалту
А) көміртектің жануы  Б) пульсациялық масса жоғалту және ақ ергежейліге көшу
Б) пульсациялық масса жоғалту және ақ ергежейліге көшу
|
(5  )≲ )≲ 
| Ядроның сығылуы+ асқынжаңа+нейтронды жұлдыз (ақ ергежейлі) |
(60 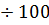 )≲ )≲ 
| Тұрақсыздық |
Астрономиялық бақылаулардың нәтижесінде, Галактикадағы "жойылған" жұлдыздарды есепке алып, қазіргі кездегі Галактикалдағы компактты жұлдыздардың тығыздығын және жалпы санын біле аламыз. Осындай бақылаулардың нәтижесінде, қазіргі кезде Галактикадағы басқа жұлдыздар сияқты компактты денелердің көп екендігіне көз жеткізуге болады (3 кесте).
3 кесте. Компактты денелердің сипаттық белгілері[33]
| Обьект | Масса, M | Радиус, R | Орташа тығыздығы, 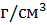
| Беттік потенциал, GM/R 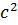
|
| Күн | 
| 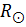
| 
| |
| Ақ ергежейлі | 
| 
| 
| 
|
| Нейтронды жұлдыз | 
| 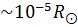
| 
| 
|
| Қара құрдым | 
| 2GM/ 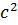
| 
| 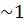
|
Қара құрдымды ешқандай да жарық тастап кете алмайды. Сондықтан да, оңашаланған қара құрдым бақылаушыға қара болып көрінеді.
Ал, нейтронды жұлдыздар, кері бета-ыдырау процесі нәтижесінде электрондар мен протондар жойылып, көп бөлігі нейтрондардан тұратындықтан өз атауын алды. Нейтронды жұлдыздар деп аталудың себебі, оның құрамының көп мөлшерін кері вета ыдырау реакциясының әсерінен протондар мен электрондар жойылып, тек нейтрондардың құрауы. Жұлдыздардың дамуының соңы нәтижесі болып нейтронды жұлдыздар болып табылады. Компактты жұлдыздардың пайда болуының негізгі факторы болып, жарылған жұлдыздың массасы болып табылады.
Ақ ергежейлілерді, ұзақ уақыт аралығында болатын суу процесінен кейін оптикалық телескоп көмегімен бақыласа болады. Нейтронды жұлдыздарды импульсты радиобастаулар немесе рентген шашыраудың периодты көзі ретінде бақыласа болады.
2.2 Ақ ергежейлілер теориясының дамуы
Қазіргі жұлдыздар дамуының теориясы бойынша, ақ ергежейлілер орта және кіші массалы жұлдыздардың соңғы даму кезеңінде пайда болады. Орталық аумақта кәрі жұлдыздың барлық сутегісі жанып біткенде, оның ядросы сығылуы және толықтай жанып бітуі тиіс. Сыртқы қабықтары қатты созылып, эффективті температурасы төмендеп, қызыл алыпқа айналады. Пайда болған жұлдыздың қабықшасы ядромен әлсіз байланысқан. Нәтижесінде, ол кеңістікте сейіледі. Кейін, қызыл алыптың орнында көп бөлігі гелийден тұратын өте жанғыш және компактты жұлдыз - ақ ергежейлі пайда болады. Өзінің жоғарға температурасына байланысты, ол ультракүлгін аралықта сәуле шығарады және қабықшада таралатын газды иондайды. Ақ ережейлілер- шамамен Күннің массасына тең, радиусы - 5000км, ал орташа тығыздығы- шамамен 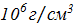 тең компактты денелер [34]. Бұл жұлдыздар өздерінің ядролық жануын аяқтап, суу процесі үстінде және жылулық энергиясын бітіруде. Ақ ергежейлілерде гравитация азғындалған электрондардың қысымына төтеп береді.
тең компактты денелер [34]. Бұл жұлдыздар өздерінің ядролық жануын аяқтап, суу процесі үстінде және жылулық энергиясын бітіруде. Ақ ергежейлілерде гравитация азғындалған электрондардың қысымына төтеп береді.
Енді бізге ақ ергежейлілердің асқын электрондардың гравитациясына төтеп бере алатындығы белгілі. Мысалы, Сириус қос жүйедегі Сириус В ақ ергежейлінің массасы қос жүйенің орбитасына Кеплердің 3- ші заңын қолдану арқылы анықтады. Ертеректе оның массасын 0,75- 0,95 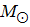 аралықта деп есептеді. Жарықтылығы Күннің 1\360 жарықтылығындай болды. 1914 жылы У.С.Адамс, Сириус В жұлдызын, спектрлері жағынан өзінің нормаль серігі Сириус А жұлдызына ұқсайтын ақ жұлдыз деп айтты. Осындай спектралды өзгерістердің нәтижесінде, жұлдыздың эффективті температурасы 8000К, радиусы 18800км [35].
аралықта деп есептеді. Жарықтылығы Күннің 1\360 жарықтылығындай болды. 1914 жылы У.С.Адамс, Сириус В жұлдызын, спектрлері жағынан өзінің нормаль серігі Сириус А жұлдызына ұқсайтын ақ жұлдыз деп айтты. Осындай спектралды өзгерістердің нәтижесінде, жұлдыздың эффективті температурасы 8000К, радиусы 18800км [35].
Ақ ергежейлілерге тән қасиеттер:
- радиусы Күннің радиусынан кіші болғанда, олар массасы жағынан қаты айырмашылықта болмайды;
- тығыздығы  ;
;
- жарықтылығы өте аз болады, Күннің жарықтылығынан жүз есеге дейін кіші болады.
Радиусының кіші болғанына байланысты, олардың температурасы жоғары болады және аз жарықтылыққа ие болады. Ақ ергежейлілердің орталық бөлігіндегі жылулық энергия 15000К төмен температурада кристалдық тор түзетін иондардың тербелісінде орналасқан. Басқаша айтқанда, ақ ергежейлілер - жанып тұрған алып кристалдар. Ақ ергежейлілердің айқындылығы және жылуөткізгіштігі жоғары болады. Бұл жұлдыздардың айқындылығы Паули принципімен анықталады. Себебі, жарықтың жұтылуы электрондардың бір орбитадан екінші бір орбитаға өткендегі күйіне байланысты. Азғындалған газдың жылуөткізгіштігі жоғары болады. Мысал ретінде, қарапайым металдарды айтсақ болады. Ақ ергежейлілілердің айқындылығы мен жылуөткізгіштігіне байланысты, олар температураның өзгеруіне жол бермейді. Ал, мұндай жағдай орын алса, ол тек азғындалмаған аймақтың сыртқы қабықшасында ғана болады. Ақ ергежейлілер аз да болса сәулеленеді. Сутегі - ақ ергежейлілерде кездеспейді десе болады, себебі, олар жұлдыздың даму барысында жанып кетеді. Бірақ, спектроскопиялық бақылаулар ақ ергежейлілердің сыртқы қабатында сутегі болатынын көрсетеді.
Ақ ергежейлілер туралы теорияны Артур Эддингтон жалғастырды. "Жұлдыздардың ішкі құрылымы" кітабында Эддингтон Сириус В жұлдызы туралы: "Массасы Күннің массасы тең және радиусы Уран радиусынан кіші жұлдыз бар" деп айтты [36]. Сонымен қатар өзінің кітаптарында, Сириус В жұлдызындағы спектр сызықтарындағы қызыл ығысу туралы айтты. Жалпы салыстырмалы теориясын пайдаланы отырып анықталғын қызыл ығысу нәтижесінде M\R қатынасын анықтай аламыз. Эддингтонның қызыл ығысуы көмегімен ақ ергежейлілердің компактты табиғаты анықталды. Қарастырылып отырған жұлдыздың тығыздығы платинаға қарағанда 2000 есе тығыздау, ал кез келген обьекттің газ аккрециясының әсерінен қара құрдым пайда болуы мүмкін.
Оның айтуынша, Ақ ергежейлілер Әлемде жиі кездесуі керек. Сол уақытта Күнге жақын орналасқан үш бірдей ақ ергежейлі жұлдыз кездесті. Эддингтон мынадай тұжырым жасады: "Аса жоғары тығыздық кезінде қарапайым газды жұлдыздар молекуланың мөлшеріне байланысты жойылады, және менің ойымша ақ ергежейлілер өздерін идеал газ сияқты ұстамайды". 1926 ж тамыз айында Дирак Фермидің алған мәліметімен Ферми- Дирак статистикасын тұжырымдады. Осы жылдың желтоқсан айында Фаулер Ферми- Дирак статистикасын пайдаланып компактты жұлдыздарды былай түсіндірді: ол гравитациялық коллапсты ұстап тұрған қысымды азғындалған электрондардың қысымымен теңестірді [37].
1930 ж Чандрасекаро азғындалған электрондар қатысатын жалпы салыстырмалы теорясы ескерілген ақ ергежейлілердің моделін жасады [38]. Сонымен қатар, ақ ергежейлілердің максимал массасы 1,4 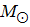 тең екендігін айтты. Ал нақты массасы химиялық құрамына байланысты. Массасы 1
тең екендігін айтты. Ал нақты массасы химиялық құрамына байланысты. Массасы 1 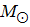 аспайтын ақ ергежейлілердің массасы мен радиусы арасындағы қатынасты анықтаудағы жалпы салыстырмалы теорияның рөлін ең алғыш рет Каплан талқылады. Оның қорытындысы: "Ақ ергежейлілердің радиусы 1,1·
аспайтын ақ ергежейлілердің массасы мен радиусы арасындағы қатынасты анықтаудағы жалпы салыстырмалы теорияның рөлін ең алғыш рет Каплан талқылады. Оның қорытындысы: "Ақ ергежейлілердің радиусы 1,1·  км- ден аз болғанда динамикалық тұрақсыздық болады".
км- ден аз болғанда динамикалық тұрақсыздық болады".
Нейтрондар ашылғаннан кейін, кері бетта- ыдыраудың нәтижесінде, өте жоғары тығыздық кезінде электрондар протондармен әсерлеседі, және нейтрондар пайда болады. Кейіннен ақ ернежейлілерде бетта- ыдырау процесі болатыы анықталды. Шацман, Гаррисон, Ваканно және Уилер кері бетта- ыд
Дата добавления: 2015-10-29; просмотров: 590 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Интересные факты | | | ГЛАВА 1. ИССЛЕДОВАТЕЛЬСКИЕ ПОДХОДЫ К ИЗУЧЕНИЮ ПРЕСТИЖНОГО ПОТРЕБЛЕНИЯ СТУДЕНТОВ КАК СОЦИАЛЬНОГО ФЕНОМЕНА. |