Использование функций МОБР, мопред и мумнож

1. Найдите матрицу, обратную данной:

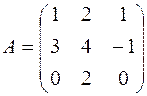
Для этого:

· введите элементы матрицы в диапазон ячеек А1:С3;

· для получения обратной матрицы выделите несмежный диапазон ячеек такого же размера, например E1:G3, и введите формулу массива {=МОБР(А1:С3)}. Для заключения формулы в фигурные скобки после ввода формулы нажмите клавиши CTRL+Shift+Enter.

2. Вычислите определитель матрицы А. Для этого выделите любую свободную ячейку, например А5, и введите формулу

=МОПРЕД(А1:С3)

3. Вычислите произведение матрицы А на матрицу В, где

; .

Для этого:

· введите элементы матрицы А в диапазон ячеек А10:С11;

· введите элементы матрицы В в диапазон ячеек А13:С15;

· выделите диапазон ячеек с таким же числом строк, как массив А, и с таким же числом столбцов, как массив В, например, E10:G11 и введите формулу

{=МУМНОЖ(А10:С11; А13:С15)};

· нажмите CTRL+Shift+Enter.

4. Решите систему линейных уравнений с 3-мя неизвестными

(1)

методом обратной матрицы.

Обозначим

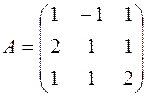;(2)

; .

Решение системы (1) в матричной форме имеет вид АХ = В,

где: А – матрица коэффициентов;

Х – столбец неизвестных;

В – столбец свободных членов.

При условии, что квадратная матрица (2) системы (1) невырожденная, т.е. ее определитель | А | ¹ 0, существует обратная матрица А . Тогда решением системы методом обратной матрицы будет матрица-столбец X = A B. Найдем это решение. Для этого:

· Найдем определитель | А | = 5 (см. п. 2). Для этого активизируем новый рабочий лист и введем элементы матрицы коэффициентов А в диапазон ячеек А1:С3. Выделим любую свободную ячейку, например А5, и введем формулу

=МОПРЕД(А1:С3).

· Так как | А | ¹ 0, то матрица А – невырожденная, и существует обратная матрица А .Найдем обратную матрицу. Для этого выделим несмежный диапазон ячеек такого же размера, что и матрица А, например E1:G3, и введем формулу массива {=МОБР(А1:С3)}.

· Найдем решение системы в виде матрицы-столбца

X = A B.. Для этого введем элементы матрицы В в диапазон ячеек E6:E8, выделим диапазон ячеек с таким же числом строк, как массив А , и с таким же числом столбцов, как массив В, например, G6:G8 и введем формулу массива

={МУМНОЖ(E1:G3; E6:E8)};

Получим:

,

т.е. решение системы (4; 2; 1).

Дата добавления: 2015-10-29