Закон сохранения момента импульса.

Билет №8.

Момент импульса.

Моментом импульса (количества движения) материальной точки А относительно неподвижной точки О называется физическая величина, определяемая векторным произведением:

где r - радиус-вектор, проведенный из точки О в точку A, p =m v - импульс материальной точки (рис. 1); L - псевдовектор, направление которого совпадает с направлением поступательного движения правого винта при его вращении от r к р.

Рис.1

Модуль вектора момента импульса

где α - угол между векторами r и р, l - плечо вектора р относительно точки О.

Моментом импульса относительно неподвижной оси z называется скалярная величина L_z, равная проекции на эту ось вектора момента импульса, определенного относительно произвольной точки О данной оси. Момент импульса L_z не зависит от положения точки О на оси z.

При вращении абсолютно твердого тела вокруг неподвижной оси z каждая точка тела движется по окружности постоянного радиуса r_iсо скоростью v_i. Скорость v_i и импульс m_iv_i перпендикулярны этому радиусу, т. е. радиус является плечом вектора m_iv_i. Значит, мы можем записать, что момент импульса отдельной частицы равен

(1)

и направлен по оси в сторону, определяемую правилом правого винта.

Монет импульса твердого тела относительно оси есть сумма моментов импульса отдельных частиц:

Используя формулу v_i = ωr_i, получим

т. е. (2)

Момент силы.

Итак, для равновесия тела, закрепленного на оси, существенна не сама величина силы, а произведение проекции силы на направление, перпендикулярное к радиусу, проведенному к точке приложения силы, на расстояние этой точки от оси. Это произведение будем называть моментом силы относительно данной оси или просто моментом силы (рис. 116). Моменты разных сил, приложенных к одной точке, равны, если равны проекции этих сил на направление, перпендикулярное к радиусу данной точки (рис. 117).

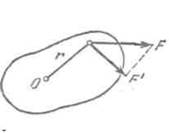
Рис. 116. Момент силы F paвен произведению ее проекции F' на расстояние r.

Рис. 117. Силы F, F₁, F₂ и F₃ имеют одинаковые моменты отноcительно оси О.

Условимся считать момент силы положительным, если эта сила, действуя в отдельности, вращала бы тело по часовой стрелке, и отрицательным в противоположном случае (при этом нужно заранее условиться, с какой стороны мы будем смотреть на тело). Например, согласно рис. 118, силам F₁ и F₂ следует приписать положительный момент, а силе F₃— отрицательный.

Моменту силы можно дать еще и другое определение. Момент силы F на рис. 119 есть M=rF'. Опустим перпендикуляр d из точки О на направление силы. Прямоугольные треугольники на чертеже подобны, ибо их соответственные углы равны. Следовательно, или F'r=Fd.

Рис. 118. Моменты сил F₁ и F₂ положительны, момент силы F₃ отрицателен.

Рис. 119. Момент силы можно выразить через силу и плечо силы, M=Fd.

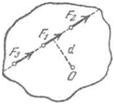
Рис. 120. Равные силы F₁, F₂, F₃ с одинаковым плечом d имеют равные моменты относительно оси О.

Следовательно, M=Fd, т. е. момент силы равен произведению силы F на длину перпендикуляра d, опущенного из оси на направление силы.

Длину перпендикуляра, опущенного из оси на направление силы, называют плечом силы. Значит, момент силы равен произведению величины силы на плечо силы. Ясно, что перенесение точки приложения силы вдоль ее направления не меняет ее момента (рис. 120). Если направление силы проходит через ось вращения, то плечо силы равно нулю; следовательно, равен нулю и момент силы этом случае сила не вызывает вращения тела: сила, момент которой относительно данной оси равен нулю, не вызывает вращения вокруг этой оси.

Пользуясь понятием момента силы, мы можем по-новому сформулировать условия равновесия тела, закрепленного на оси и находящегося под действием двух сил. Как мы видели, для равновесия необходимо, чтобы силы стремились вращать тело в противоположных направлениях и чтобы произведения сил на их расстояния до оси были равны. Значит, при равновесии моменты обеих сил должны быть равны по величине и противоположны по знаку. Таким образом, для равновесия тела, закрепленного на оси, алгебраическая сумма моментов действующих на него сил должна быть равна нулю.

Так как момент силы определяется произведением величины силы на плечо, то единицу момента мы получим, взяв силу, равную единице, плечо которой также равно единице. Значит, в системе СИ единицей момента силы является момент силы в 1 н, действующей на плече в 1 м, т. е. 1 н*м, в системе СГС —1 дин*см, в системе МКСС— 1 кГ*м. Пользуясь данными § 45, найдем соотношения между этими единицами:

1 дин*см = 10^-7 н*м; 1 кГ*м = 9,8 н*м.

Если на тело, закрепленное на оси, действует много сил, то, как показывает опыт, условие равновесия остается тем же, что и для случая двух сил: для равновесия тела, закрепленного на оси, алгебраическая сумма моментов всех сил, действующих на тело, должна быть равна нулю.

Можно ввести понятие об уравновешивающем моменте, о равнодействующем моменте и о сложении моментов сил, действующих на тело, закрепленное на оси, подобно тому как были введены понятия об уравновешивающей силе, о равнодействующей силе и о сложении сил. Так, результирующим моментом нескольких моментов, действующих на тело (составляющих моментов), будем называть алгебраическую сумму составляющих моментов. Под действием результирующего момента тело будет двигаться (вращаться вокруг оси) так же, как оно вращалось бы при одновременном действии всех составляющих моментов. В частности, если результирующий момент равен нулю, то тело, закрепленное на оси, либо покоится, либо вращается равномерно.

Закон сохранения момента импульса.

Суммарный момент импульса замкнутой системы относительно неподвижной оси вращения не изменяется с течением времени.

J*w = const

. Два одинаковых шара насажены на гладкий горизонтальный стержень, но которому они могут скользить. Шары сближают и соединяют нитью. Затем всю установку приводят во вращение вокруг вертикальной оси, предоставляют ее самой себе и пережигают нить. Шары, естественно, разлетаются к концам стержня. Угловая же скорость установки при этом резко уменьшается.

Опыт с шарами

Наблюдаемый эффект является прямым следствием закона сохранения момента импульса, так как данная установка ведет себя, по существу, как замкнутая, так как внешние силы компенсируют друг друга, так как силы трения в оси малы. Для количественной оценки изменения угловой скорости будем считать, что масса всей установки практически сосредоточена в шарах, а их размеры пренебрежимо малы. Тогда из равенства моментов импульса шаров относительно точки C в начальном и конечном состояниях системы следует

Отсюда видно, что с увеличением расстояния шаров от оси вращения угловая скорость установки уменьшается обратно пропорционально квадрату этого расстояния. И наоборот, если бы уменьшалось под действием каких-либо внутренних сил, угловая скорость установки увеличивалась бы. Этот эффект имеет общий характер, и его широко используют спортсмены в своих выступлениях, например, фигуристы и гимнасты.

Дата добавления: 2015-10-23