Эллиптические кривые над конечными полями

Определенные выше операции над точками кривых могут быть распространены на случай произвольного поля. Необходимые формулы могут быть получены, если воспользоваться алгебраическими выражениями для геометрических понятий - "прямая", "вертикальная прямая", "касательная".

В нашей лабораторной работе будем рассматривать только поля типа GP={0, 1, 2, …, p-1}, где p – натуральное простое число. При p>3 уравнение (1) можно преобразовать к виду:

y² = x³ + ax + b (2)

где .

Число точек на такой кривой удовлетворяет неравенству Хассе .

Среди точек кривой необходимо найти некоторую базовую точку B, обладающую тем свойством, что любая другая точка может быть получена, как кратная этой точки. Такая точка называется примитивным, или образующим элементом кривой. В действительности, для ЭК такой точки может не существовать, но должна найтись точка B, обладающая большим порядком k=ord(B) (порядок точки – это наименьшее число k такое, что kB=O –бесконечно удаленная точка). В этом случае, выбирается подгруппа ЭК, порождаемая элементом B.

Рис. 2. Сложение точек на эллиптической кривой

Введем следующие правила сложения точек на эллиптической кривой:

• Точка O выступает в роли нулевого элемента. Так, O = -O и для любой точки Р на эллиптической кривой Р + O = Р.
• Вертикальная линия пересекает кривую в двух точках с одной и той же координатой х - скажем, S = (x, y) и T = (x, -y). Эта прямая пересекает кривую и в бесконечно удаленной точке. Поэтому Р₁ + Р₂ + O = O и Р₁ = -Р₂.
• Чтобы сложить две точки P и Q (см. рис. 2) с разными координатами х, следует провести через эти точки прямую и найти точку пересечения ее с эллиптической кривой. Если прямая не является касательной к кривой в точках P или Q, то существует только одна такая точка, обозначим ее S.

Согласно нашему предположению P + Q + S = О.

Следовательно, P + Q = -S или P + Q = T

Если прямая является касательной к кривой в какой-либо из точек P или Q, то в этом случае следует положить S = P или S = Q соответственно.

• Чтобы удвоить точку Q, следует провести касательную в точке Q и найти другую точку пересечения S с эллиптической кривой. Тогда Q + Q = 2 × Q = -S.

Введенная таким образом операция сложения подчиняется всем обычным правилам сложения, в частности коммутативному и ассоциативному законам. Умножение точки Р эллиптической кривой на положительное число k определяется как сумма k точек Р.

Дадим формулы для вычисления суммы двух точек A (x₁, y₁) и B (x₂, y₂) на ЭК:

(3)

где

Координаты удвоенной точки 2A (или суммы A+B при совпадении точек A и B), определяются по тем же формулам (3), но коэффициент λ будет вычисляться иначе:

Математическая задача, которую должен решить атакующий на шифры ЭК, есть задача дискретного логарифмирования на эллиптической кривой, и формулируется она следующим образом. Даны точки P и Q на эллиптической кривой E_p (a,b). Необходимо найти коэффициент k < p такой, что P = k × Q. Относительно легко вычислить P по данным k и Q, но трудно вычислить k, зная только P и Q.

Пример. Пусть p =23, кривая имеет уравнение , т.е. a =1, b =0.

Перебирая в цикле всевозможные значения x,y от 0 до 22 найдем множество пар точек, лежащих на этой кривой:

ЭК ={(10, 11), (13, 18), (15, 20), (9, 18), (19, 22), (1, 5), (17, 10), (18, 13), (20, 19), (16, 8), (21,17), (0, 0), (21, 6), (16, 15), (20, 4), (18, 10), (17, 13), (1, 18), (19, 1), (9, 5), (15, 3), (13, 5), (11, 13), (∞,∞)}

Таким образом, порядок числа точек на кривой равен 24 (в конец списка добавлена бесконечно удаленная точка).

Вычислим, например, сумму точек A (13; 18) и B (9; 5). По формулам (3) имеем:

.

Для нахождения обратного элемента используем расширенный алгоритм Евклида, подставляя на входе p =23 и b =4:

P	B	P mod B	P div B	x	y
				-1
					-1

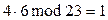В правом верхнем углу получим значение . Действительно, . Тогда, . Вычислим координаты суммы точек:

Значит, сумма точек A (13; 18) и B (9; 5) равна C (13; 5). Можно проверить, что эта точка присутствует на ЭК нашего примера.

Рассмотрим три способа использования эллиптических кривых в криптографии.

Дата добавления: 2015-10-29