Раскраски графов

Пусть G=(V,E) – граф

Опр. Раскраской графа называется такое приписывание цветов его вершинам, что никакие 2 смежные вершины не получают одинакового цвета.

Т. Образом мн-во вершин одного цвета явл. Независимым мн-вом

Опр. Хроматическим числом X(G) наз. Min числом цветов, требующихся для раскраски графа G

Если X(G)=k, то граф Gназыв. К-хроматическим

Задача раскраски вершин и ребер графа занимает важнейшую роль в истории развития графов.

К построению раскрасок сводится ряд задач,

напр: 1.задача построения расписания 2.распределение оборудования

Легко найти хроматические числа для нек-х известных графов X() = n, X()=1, X(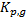) = 2, X(T) = 2 (дерево)

Эффективные методы определения хромат числа произвольных графов пока не наидены

В такой ситуации актуальны оценки хром. Числа терминах более или менее просто вычислительных параметров графа Обозначим граф Р(G) - наибол. Из степеней графа G

Т1. Для любого неориент. Графа выполрав-во X(G) P(G) +1

Проблема раскраски планарных явл. Одной из самых значимых проблем в теории графов.

Она возникла из задач раскраски геогр. Карты, любые 2 соседние страны должны быть раскрашены в различные цвета. Эта задача сводится к раскраске планарных графов

В 1879г Кэпи сформулировал гипотезу 4-х красок. Всякий планарный граф 4-х раскрашиваемый. Попытки доказательств в 1890г привели к теореме Хи вуда

Т2. Всякий планарный граф 5-раскрашиваемый (задача о 5 красках)

Трудность проблемы 4-х красок привела к появлению большому кол-ву равносильных ей формулировок.

В 1960г эта проблема была сведена к исследованию большого, но конечного множ. Так называемых неустранимых конфигураций, число которое оказалось 1482

В 1976 г науч. Коллективу под руководством Аппеля и Хейкена удалось с исп. ЭВМ правильно раскрасить все графы из множ. Неустранимых конфигураций, затратив на это около 2-х тысяч часов машинного времени.

Т.об. можно считать, что формально гипотеза 4-х красок доказана. Алгоритм последовательной раскраски графа в общем случае не приводит к min раскраске.

Только для некоторых классов графов (полных k-дольных) последовательная раскраска минимальная

Дата добавления: 2015-10-28