Задачи для самостоятельного решения.

X

Y1

Y2

Y3

Y4

Y5

Y6

Y7

Y8

Y9

Y10

Y11

Y12

Справа приведена таблица из двенадцати вариантов функций Y(X). Для каждой из них известны восемь точек. Для своего варианта сделать следующее:

· Найти уравнения регрессии первой, второй и третьей степени, используя технологию, рассмотренную на рис. 3-1.

· Для Х=10 вычислить значение Y по этим уравнениям.

· Построить их кривые, аналогичные рис. 3-3.

· Построить аппроксимирующие зависимости, используя только средства деловой графики Excel.

4. Множественная линейная регрессия. Ранее нами была рассмотрена технология нахождения парной линейной регрессии Y(X). На практике, конечно, на исследуемую систему влияет не один, а несколько (или даже много) параметров. В этом случае необходимо использовать уже множественную регрессию, т.е. найти функцию вида Y(X,Z, …). Геометрическим представлением тогда будет не прямая линия, а плоскость или гиперплоскость.

Найдем сейчас коэффициенты уравнения линейной регрессии, для двух влияющих переменных Y(X,Z). Такое уравнение будет выглядеть так Y=a+bX+cZ. Таким образом, нам нужно найти три коэффициента А, В и С.

Поступим уже известным нам образом. Искомые коэффициенты будем искать (рис. 4-1) в клетках A2, B2, C2. Первоначально они пусты (т.е. коэффициенты a, b, c пока считаем равными нулю). В столбцы A, B, C (область A4:C10) внесем известные нам значения X, Y, Z. В столбец D внесем формулы для вычисления значений, полученных с помощью пока не найденной функции линейной регрессии Yл (D4=A$2+B$2*A4+C$2*B4). В клетку D11 – формулу (=СУММКВРАЗН(C4:C10;D4:D10)) суммирующую квадраты разностей двух векторов (у нас Y и Yл). Теперь вызываем Поиск решения, где задаем: установить в ячейке D11 минимальное значение, изменяя ячейки A2:C2. Результат мы видим в таблице – искомая функция такова Yл=9,8-0,7X-0,7Z.

Теперь построим диаграмму (рис. 4-2), отображающую наше решение. Она будет использовать данные из области G3:M6. Создадим ее. В столбец F внесем значения X, в строку 2 – значения Z. Клетки заполним формулами вычисляющими Yл для значений X и Z, на пересечении которых она находится (G3=$A$2+$B$2*$F3+$C$2*G$2). Затем строим диаграмму (Поверхность (проволочная)) из данных, находящихся в области G3:M6.

Уравнение множественной регрессии можно получить и, используя один из прилагаемых к Excel, дополнительных модулей – Пакет анализа. С его помощью можно получить коэффициенты уравнения и его статистические характеристики.

	A	B	C	D	E	F	G	H	I	J	K	L	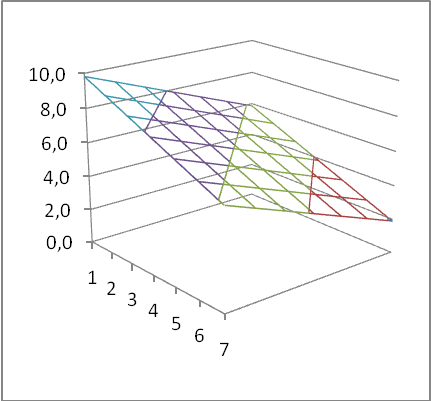Рис. 4-2   M
	a	b	c
	9,8	-0,7	-0,7			x\z
	X	Z	Y	Yл			9,8	9,2	8,5	7,8	7,2	6,5	5,9
				9,8			9,2	8,5	7,8	7,2	6,5	5,9	5,2
				8,5			8,5	7,8	7,2	6,5	5,9	5,2	4,5
				7,2			7,8	7,2	6,5	5,9	5,2	4,5	3,9
				5,9			7,2	6,5	5,9	5,2	4,5	3,9	3,2
				4,5			6,5	5,9	5,2	4,5	3,9	3,2	2,6
				3,2			5,9	5,2	4,5	3,9	3,2	2,6	1,9
				1,9
	Сумма D^2:	2,0								Рис.	4-1

Дата добавления: 2015-10-28