Формирование последовательности случайных чисел, распределенных по показательному закону.

В настоящее время известно множество алгоритмов, генерирующих случайные числа, с заданным законом распределения. Такие числа называют псевдослучайными. Познакомимся с одним из них. Для того чтобы получить последовательность случайных чисел с заданным законом распределения необходимо:а) получить равномерно распределенные случайные числа R в промежутке (0,1). В состав стандартных функций многих алгоритмических языков входят стандартные функции, генерирующие RÎ(0,1); б) подставив в соответствующую формулу преобразования полученные числа, смоделировать случайные числа с заданным законом распределения. V= f(R).Для каждого закона распределения существует иногда несколько формул преобразований. Приведем некоторые формулы преобразования для наиболее употребляемых законов распределений: б) для показательного закона распределения где l - плотность потока, RÎ(0,1);

7. Жүйлерді модельдеудің кезеңдері Жүйелерді модельдеу кезеңдері S жүйесін модельдеу үш негізгі кезеңнен тұрады: 1) Жүйенің концептуальды моделін құру және оны формализациялау.2) Жүйе моделін алгоритмдеу және оны машиналық жүзеге асыру.3) Жүйені модельдеу нәтежиелерін алу және интерпретациялауӘр кезеңге нақтырақ тоқталалық:Бірінші кезең келесі ішкі кезеңдерден тұрады.Модельдеу мақсатын анықтау.Тапсырманың құрылымы.Тапсырмаға талдау.Бастапқы ақпараттарға талаптарды анықтау және оны жинақтауды ұйымдастыру.

Параметрлер мен айнымалыларды анықтау.Жүйе тиімділігін бағалау критерилерін негіздеу.Концептуальды модель - бұл абстрактылы модель, жүйе құрылымын, оның элементтерінің қасиеттерін анықтайды және олардың арасында салыстыруды жүзеге асырады.2) ЕКІНШІ КЕЗЕҢ

Жүйе модельдерін алгоритмдеу және машиналық жүзеге асыру.2.1. Модельдің логикалық сұлбасын құру (блок-сұлба)2.2. Математикалық қатынастарды функциялар түрінде алу.2.3. Жүйе моделінің сәйкестігін (адекваттығын) тексеру, яғни оның адекваттылығын тексеру.2.4. Модель алгоритмін жүзеге асыратын программа әзірлеу.3) ҮШІНШІ КЕЗЕҢЖүйені модельдеу нәтежиелерін алу және интерпретациялау.3.1. Жүйе моделімен машиналық тәжірибені жоспарлау.3.2. Есептеу жабдықтарына талаптарын анықтау.3.3. Жұмыс есептеулерін жүргізу.

3.4. Жүйені модельдеу нәтежиелерін талдау.3.5. Модельдеу нәтежиелерін көрсету (графиктер, диаграммалар, кестелер және т.б. түрінде)

8.Жаппай қызмет ету жүйелері туралы жалпы мәліметтер (ЖҚЖ).

Математикалық модельдеудегі маңызды бөлімдердің бірі жаппай қызмет көрсету жүйелерінің теориясы болып табылады. Теорияның негізін қалаушы Дат математигі А.К.Эрланг..Әрбір жаппай қызмет көрсету жүйесі өз құрылымына қызмет көрсетуші құрылғылардың бірнеше санын қамтиды, ол қызмет көрсету каналдары деп аталады. Каналдар ролін түрлі операцияларды орындайтын (кассирлер,операторлар, сатушылар) түрлі аспаптар, байланыс желілері, тұлғалар ойнай алады.Жаппай қызмет көрсету жүйесі бір каналдық немесе көпканалдық болуы мүмкін.Әрбір ЖҚКЖ уақыттың кездейсоқ бір сәтінде жүйе кірісіне келіп түсетін тапсырыстардың кейбір ағынына қызмет көрсетуге арналған. Тапсырыстарға қызмет көрсету кездейсоқ уақытқа созылады. Тапсырысқа қызмет көрсетілгеннен кейін канал босайды және келесі тапсырысты қабылдауға дайын тұрады.Тапсырыстар ағынының және оларға қызмет көрсету уақытының кездейсоқтық сипаты ЖҚКЖ-ның жүктемесін қалыпты жағдайдан ауытқытып жібереді: уақыттың қандай да бір аралығында кіріске тапсырыстар жиналып қалады, қызмет көрсету кезегіне тұрады, болмаса жүйені тастап кетеді. Осылайша, жалпы ЖҚКЖ-н келесідей негізгі элементтерге бөлуге болады:

Тапсырыстардың кіріс ағыны;

Кезек;

Қызмет көрсету каналдары;

Қызмет көрсетілген тапсырыстар ағыны;

Қызмет көрсетілмеген тапсырыстар ағыны;

ЖҚКЖ мыналар мысал бола алады: телефон станциялары, билет кассалары, дүкендер, шаштараздар және т.б.

Әрбір ЖҚКЖ - тапсырыстар ағынының сипаттамалары, қызмет көрсету каналдарының саны және олардың өнімділігі, жұмысты ұйымдастыру ережелері сияқты параметрлерге сәйкес қызмет көрсетудің белгілі бір тиімділігін қамтиды. Жаппай қызмет көрсету теориясының нысаны - тапсырыстар ағынының сипаттамалары, каналдар саны және олардың өнімділігі, ЖҚКЖ жұмыс ережелері және қызмет көрсету тиімділігі арасында тәуелділік орнату болып табылады.

9) Жаппай қызмет ету жүйелері теориясының мақсаттары. ЖҚЖ-ның мақсаттары: ЖҚЖ-ның әртүрлі жағдайының ықтималдығын табу,сонымен бірге берілген параметрлердің арасындағы тәуелділікті (n каналдар саны, тапмырыстар ағынының екпінділігі және т.б.),ЖҚЖ жұмысының сапасының сипаттамаларын анықтау.ЖҚЖ жұмысының сапасының сипаттамалары:уакыт бірлігінде қызмет көрсетілетін тапсырыстардың орташа саны немесе ЖҚЖ-ң өткізу мүмкіндігі;қызмет көрсетуден бас тарту ықтималдығы;ЖҚЖ-дағы тапсырыстардың орташа саны;кезектегі тапсырыстардың орташа саны;тапсырыстардың кезекте болуының орташа саны;тапсырыстардың ЖҚЖ-да болу уақытының орташа мәні;тапсырыстардың кезекте болу уақытының орташа мәні;бос емес каналдардың орташа саны.

10) Оқиғалар ағыны. Оқиғалар ағынының қасиеттері. Оқиғалар ағыны кездейсоқ уақыт мезетінде бірінен соң бірі келіп тұратын бірдей оқтғалар тізбегі.Оған мысал:телефон станциясына келіп түсетін шақырулар саны, компьютердегі ақаулар ағыны, теміржол станциясына келіп түсетін жүктер ағыны.Оқиғалар ағыны түрлі қасиеттерге ие. Осы қасиеттерге қарай ағындарды бірнеше топқа бөлеміз. Реттелген ағын (регулярный поток) бірдей тең уақыт аралығы арқылы бірінен соң бірі келіп түсетін оқиғалар ағыны.Мұндай ағындар тәжірибеде сирек кездеседі.Телекомм. жүйелерде оқиғалардың келіп түсу мезеті және олардың арасындағы уақыт аралығы кездейсоқ болады. Стационарлық ағын (тұрақты ағын) дегеніміз егер t уақыт аралығында оқиғаның қандай бір санының пайда болу ықтималдығы осы аралықтың ұзындығына тәуелді болса, ал осы аралықтың уақыт бірлігінің қай жерде орналасқанынан тәуелсіз болса орындалады.Ординарлық ағын дегеніміз бір уақыт мезетінде 1-ден көп оқиғаларың келіп түсу ықтималдығы өте аз болатын ағын немесе ординарлық ағында бір уақыт мезетінде бір ғана оқиға келіп түсе алады.Телекомм. желілерінде ағындар әрқашанда жалғызданған болады. Кейінді ықпалдықсыз ағын (поток без последствия)дегеніміз келесі шарттарда орындалады:- егер оқиғалар ағының ықтималдың сипаттамалары тек осы шақтан тәуелді болып, өткен шақтардан тәуелсіз болса, онда оқиғалар ағының кейінді ықпалдықсыз деп атайды.()

11) Қарапайым оқиғалар ағыны. Пуассон формуласы.

Тұрақты – жалғызданған ағын кейінгі ықпалдықсыз ағынды қарапайым ағын (простейший поток) немесе Пуассон ағыны деп атайды.Ағын Пуассон үлестірім заңына бағынғандықтан Пуассон ағыны деп аталады.

-t уақыт ішінде k-оқиғалардың келіп түсуінің ықтималдығы; ағынның екпінділігі.Кез-келген ағынның параметрі дегеніміз:

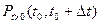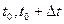- ()-уақыт аралығында ең болмаса бір оқиғаның келіп түсу ықтималдығы.Оқиғалар ағынының екпінділігі дегеніміз уақыт бірлігінде келіп түсетін оқиғалардың орташа саны().Тұрақты ағында =const, қарапайым ағында Қарапайым ағынның сипаттамалары мен қасиеттері: 1.Егер Z-қарапайым ағында келіп түсетін тапсырмалардың арасындағы уақыт болса, онда Mz = Mz-математикалық үміт; -орташа квадраттық ауытқу.2.t уақыт аралығында келіп түсетін шақыруларлың санының (і) Мі мен дисперсиясы өзара тең Мі=Dі= t. Бұл қасиетті оқиғалар ағынын қарапайым екпінділігін тексергенде пайдаланады.

3.Бірнеше қарапайым ағын қосылғанда пайда болатын ағын қарапайым болды.

4.Қарапайым ағын бірнеше ағынға айрылғанда п.б. ағындар қарапайым болады.

Қарапайым ағында тапсырыстар арасындағы аралықтар көрсеткіш заңмен үлестіріледі. GENERATE (Exponential(1,0,300))

12) ЖҚЖ модельдерінің символдық белгіленуі (Кендалл бойынша).

Американдық ғалым Кендалл зерттелетін модель туралы бастапқы мәліметтерді түсіндіру үшін келесі символдарды ұсынған.Кендалдың символикасында 6 разряд бар.1-ші разряд жүйеге келіп түсетін тапсырмалар ағынын анықтайды.2-ші разряд қызмет көрсету уақытының үлестірім заңын анықтайды.3-ші жүйенің құрылымын көрсетеді.4-ші қызмет көрсету тәртібін, 5-ші тапсырысты кезектен таңдап алу тәсілін,6-бос аспаптарды иемдену тәртібін анықтайды.Разрядтар бір-біріне көлбеу сызық (/) арқылы ажыратылады.

І-разрядта келесі символдар қолданылады:М-тапсырыстар арасындағы уақыт көрсеткіш заңымен үлестірілген (қарапайым ағын).D-тапсырыстар арасындағы уақыт тұрақты, яғни детерминантты.Gl-тапсырыстар арасындағы кез-келген үлестірім заңымен үлестірілген.

ІІ-разрядта осы символдар қолданылады,бірақ мұнда олардың қызмет көрсету уақытының қандай заңмен үлестірілгенін көрсетеді.

ІІ-разрядта еркін үлестіру G-мен көрсетіледі.

ІІІ-разряд жүйенің құрылымын көрсетеді.S-кез-келген құрылым.FM(Full Matrix)-толық қатынастағы құрылым.Кез-келген каналды ала алады.кейбір жағдайда бұл разрядта каналдардың саны көрсетіледі(V).

IV-разрядта келесі символдар қолданылады:LL-шығынсыз қызмет көрсету тәртібі, L-айқын шығындармен қызмет көрсету,W(wait)-күту мен қызмет көрсету тәртібі,R(Reattemt)-қайталау мен қызмет қөрсету.

V- разрядта келесі символдпр қолданылады.SP(same Probability)-тең ықтималды тәртіп,FF(First in-First out)-реттелген тәртіп,LF(Last in Last out)-соңғы келген тапсырысқа бірінші қызмет көрсетіледі, PR- приоритетті тәртіп.

VI-разрядта тапсырыс каналдарды таңдайды.S-тең ықтималдықты R-кездейсоқ.

Американдык галым Кендалл зерттелетiн модель туралы бастапкы малiметтердi тусiндiру ушiн келесi символдарда в разряд бар: 1-шi разряд жуйеге келiп тусетiн тапсырыстар агынын аныктайды.2-шi разряд кызмет корсету уакытынын улестiрiм занын аныктайды.3 разряд жуйенiн курылымын корсетедi.4-шi разряд кызмет корсету тартiбiн аныктайды.6-шы разряд бос аспаптарды иемдену тартiбiн анык.1-шi разрядта келесi символдар колданылады: М-тапсырыстар арасындагы уакыт корсеткiш занымен улестiрiлген. D-тапсырыстар арасындагы уакыт детерминанты. GL-тапсырыстар арасындагы уакыт корсеткiш занымен улестiрiлген. 2- разрядта еркiн улестiрiлiм G арiпiмен корсетiледi.3-разряд жуйенiн курылымын корсетедi. Егер S турса кез-келген курылым FM- толык катынастагы курылым. Кез-келген тапсырыс кез-келген каналды ала алады. (full matrix). 4-шi разрядта келесi символдар колданылады:LL- шыгынсыз кызмет корсету факторы (lassles).L айкын шыгындармен кызмет корсету.W- куту мен кызмет корсету тартiбi.(wait).R- кайталау мен кызмет корсету(Reattemt). 5-шi разрядта: SP- тен ыктималды тартiп. FF – реттелген тартiп.LF – сонгы келген тапсырыска 1-шi кызмет корсетемiз.PR- приоритеттi тартiп. 6-шы разрядта: S- тен ыктималдыкты. R-кездейсок.

Дата добавления: 2015-10-28