Сети СМО. Замкнутые и разомкнутые

В общем случае сеть СМО (Queuing Networks) можно представить в виде графа, вершинами которого являются одноканальные и многоканальные СМО (дуги определяют потоки передачи требований).

Простейшая разомкнутая или открытая сеть получается при по­следовательном соединении СМО (рис.7.1). Она еще называется многофазной СМО.

Рисунок 7.1

Различают замкнутые и разомкнутые сети. Для замкнутой веро­ятностной сети не существует внешних источников требований, то есть в ней всегда находится одно и то же количество требований. Для разомкнутой сети имеются источники требований и стоки требований.

Для расчетов сетей массового обслуживания используется теория вероятностных сетей, которая основывается на марковских и полумарковских процессах, но большинство результатов получено только для экспоненциальных законов распределения. При количестве узлов сети больше трех для расчетов используются численные приближенные методы. Операционный анализ в отличие от тео­рии массового обслуживания опирается на логику работы рассматри­ваемой или моделируемой системы. Это позволяет установить про­стые зависимости между параметрами и показателями работы систе­мы, не абстрагируясь от процессов ее функционирования.

Основная задача операционного анализа вероятностных сетей состоит в определении таких показателей, как среднее время пребывания требований в отдельных узлах сети, загрузка устройств в узлах, средние длины очередей к узлам и т.п.

Большинство результатов операционного анализа касается замкнутых сетей, когда требования, которые покидают сеть, снова возвращаются в нее. Замкнутые сети можно использовать, когда рас­сматриваемая система работает с перегрузкой. В этом случае можно считать, что вместо требования, которое покинуло систему, в систему поступает другое требование с такими же параметрами.

21. Сети СМО. Графы и матрицы передач. Теорема Джексона. В общем случае сеть СМО (Queuing Networks) можно представить в виде графа, вершинами которого являются одноканальные и многоканальные СМО (дуги определяют потоки передачи требований). Сеть СМО удобно представлять в виде графа передач (рисунок 7.2), где вершины графа соответствуют СМО, дуги указывают возможности перехода заявки из одной СМО в другую, а числа в дугах — вероятности перехода.

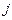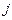Рассмотрим сеть систем массового обслуживания, которая включает M СМО и один источник заявок. Заявки, выходящие из -й системы с постоянной вероятностью , поступают в систему или покидают сеть . Из источника в -ю систему заявки поступают с вероятностью Матрицу вероятностей поступления требований из одной системы в другую называют матрицей передач:

Для графа передач, представленного на рис.7.2, матрица передач будет следующей

Дата добавления: 2015-10-28