Розміщення з повтореннями

МІНІСТЕРСТВО ОСВІТИ ТА НАУКИ УКРАЇНИ

НАЦІОНАЛЬНИЙ ТЕХНІЧНИЙ УНІВЕРСИТЕТ УКРАЇНИ

«КИЇВСЬКИЙ ПОЛІТЕХНІЧНИЙ ІНСТИТУТ»

КАФЕДРА ОБЧИСЛЮВАЛЬНОЇ ТЕХНІКИ

Протокол до

лабораторної роботи №3

Виконав:

Папуша Олександр Васильович

Факультет ІОТ

Група ІО-34

Номер залікової книжки 3418

Тема: «Комбінаторика: перестановки, розміщення, сполучення».

Мета: вивчення правил утворення комбінацій можин: перестановок,

розміщень, сполучень

Завдання лабораторної роботи

Виконати завдання 1 до лабораторної роботи за умови, що вхідні

параметри приймають такі значення:

1. Максимальне значення n дорівнює (10+NZK mod 11).

2. Значення s може змінюватися довільно від 1 до n

3. Сформувати початкову перестановку P таким чином, що кожен її

елемент вибирається випадково та без повторень чисел.

Вивчити принципи роботи алгоритму перестановок у лексикографічному

порядку. Використовуючи блок-схему, представлену на рис. 3.1. написати

програму перестановок чисел десяткової системи числення у

лексокографічному порядку.

Рис.3.1. Блок-схема алгоритму перестановок в лексикографічному порядку

Теоретичні відомості:

Перестановки

Комбінації з n елементів, які відрізняються одна від одної тільки

порядком елементів, називаються перестановками.

Перестановки позначаються символом Рn, де n — число елементів, що

входять у кожну перестановку.

Отже, число перестановок обчислюємо за формулою: Рn = n!

Розміщення

Комбінації з n елементів по m елементів, які відрізняються одна від одної

або самими елементами, або порядком елементів, називаються розміщеннями.

Розміщення позначаються символом m

Аn, де n – число всіх наявних

елементів, m – число елементів у кожній комбінації. Число розміщень можна

обчислити за формулою:

Аm = n (n -1)(n - 2) ... (n - m + 1), де 0 ≤ m ≤ n; m, n Î N.

Формулу розміщення можна записати у факторіальній формі:

Сполучення

Сполученнями називаються всі можливі комбінації з n елементів по m, які

відрізняються одна від одної принаймні хоча б одним елементом

У загальному випадку число сполучень із n елементів по m дорівнює числу

розміщень з n елементів по m, діленому на число перестановок з m елементів:

Одержимо формулу кількості сполучень у вигляді:

Розміщення з повтореннями

Розміщення з n елементів по k відображають упорядковані комбінації різних

елементів множини М, |М|=n. Часто доводиться утворювати упорядковані

комбінації з повтореннями деяких елементів.

Такі упорядковані k -комбінації називають

кортежами довжини k. Два кортежі (тобто дві загальні комбінації) вважаються однаковими, якщо вони мають однакову довжину і на місцях з однаковими номерами стоять однакові елементи.

Кортеж довжини k з n елементів називається розміщенням з повтореннями з n елементів по k.

Кількість кортежів обчислюється за формулою:

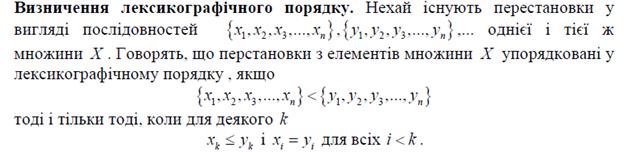
Дата добавления: 2015-10-28