Принцип непрерывности магнитного поля.

Индукция и поток вектора индукции магнитного поля

Одной из основных характеристик магнитного поля является вектор магнитной индукции - векторная величина, характеризующая магнитное поле и определяющая силу 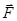, действующую на движущуюся или смещающуюся заряженную частицу со стороны магнитного поля в заданной точке. Модуль и направление вектора магнитной индукции определяется по влиянию магнитного поля на рамку с током, помещаемую в заданную точку магнитного поля.

,

где 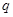- электрический заряд; - скорость заряда; - магнитная индукция однородного поля.

При изучении электромагнитной индукции невозможно обойтись без введения новой физической величины, называемой магнитным потоком. Если вектором В можно охарактеризовать магнитное поле в каждой отдельной точке пространства, то этого явно недостаточно, ибо процессы происходят в объёме и необходимо ввести понятие о величине, характеризующий магнитные явления в пространстве вблизи плоского контура.

Контур зададим нормалью n. Нормалью n называют вектор единичной длины, перпендикулярный к плоской поверхности исследуемого контура. Вектор составляет угол α с направлением вектора магнитной индукции. Пусть S - площадь поверхности плоского контура. Магнитным потоком Ф (потоком магнитной индукции) через поверхность площадью S называют величину, равную произведению модуля вектора магнитной индукции В на площадь S и косинус угла α между векторами В и n (справедливо для однородного поля):

,

где Ф - магнитный поток; В - модуль вектора магнитной индукции; S - площадь контура, внутри которого мы измеряем магнитный поток, α - угол между вектором магнитной индукции В и нормалью к плоскости контура.

В случаи неоднородного поля магнитный поток определяется из выражения

Принцип непрерывности магнитного поля.

вычислим поток через замкнутую поверхность, имеющую площадь S. Можно провести такую замкнутую линию L таким образом, чтоб в любой точке справа от L линии магнитной индукции входили в этот объем, а слева – выходили.

В каждой части поверхности S выделим очень маленькую площадь 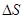. Выберем положительный обход поверхности и представим 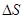вектором. Векторы этих площадок всегда направлены от поверхности. Таким образом, вектора и имеют между собой тупой угол. Следовательно, поток, пронизывающий имеет знак «-».

Угол между и - острый, поэтому поток, пронизывающий имеет знак «+».

Для каждой площади 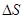справа от линии L найдется площадь 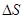слева от линии, так что суммарный поток через эти площадки = 0.

.

Перемещая площадь 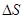вдоль линий магнитной индукции мы убеждаемся в том, что для любого положения справедливо уравнение . Это нас приводит к выводу о том, что линии магнитной индукции непрерывны и замкнуты.

Векторное поле, для которого выполняется это уравнение называется соленоидальным, а векторное поле, для которого выполняется это уравнение – вихревым.

Как охарактеризовать способность порождать вектор в каждой точке?

Дивергенция вектора характеризует возможность порождения потока в каждой точке пространства.

Предположим, что у нас есть вектор а, который пронизывает замкнутую поверхность S.

Обозначим объем, ограниченный площадью S как . Введем новую величину, которая равна: .

Эта величина характеризует способность объема порождать вектор . Устремим к нулю и выведем величину – дивергенция вектора , которая определяется этим уравнением.

Дата добавления: 2015-10-28