
|
Читайте также: |
Variant 3
1. For the triangle with the vertices А (2;5), В (–6;-4), С (6;–3) find:
a) length of the side АВ;
b) equation of the line АМ which parallel to the side ВС;
c) the equation of the hieght ВF;
d) the equation of the median AD;
e) the interior angle  ;
;
f) the coordinates of the points N and K, which divides the greater sige of the triangular into three equal parts;
g) area of the treangular АВС.
2. There are given the points М 1(1;–2;0), M 2(2;–3;2), of the plane Р 1: 2x+3y-4z-2=0,
Р 2: 2x-y+z+9=0 and lines лінії L 1:  ; L 2:
; L 2: 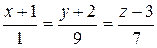 .
.
а) Write down the equation of the straight line passing through the points М 1 and M 2;
b) Find the acute angle between the lines L 1 and L 2;
c) Through the point M 2 draw the plane parallel to the plane Р 2;
d) Find the acute angle between the planes Р 1 and Р 2;
e) Find the distance from the point М 1 to the plane Р 2;
f) Through the point M 2 draw the line parallel to the line L 2;
g) Find the acute angle between the line L 2 and the plane Р 2;
h) Through the point М 1 draw the line perpendicular to the plane Р 1;
i) Write down the equation of the plane passing through the point М 1 and perpendicular to the planes Р 1 and Р 2;
j) Write down the canonic equation of the line which is the concurent of two planes Р 1 and Р 2.
3. Calculate the limits: а) 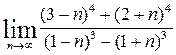 ; b)
; b) 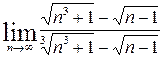 ;
;
c) 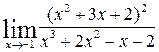 ; d)
; d) 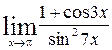 .
.
4. Calculate the limits: а)  ; b).
; b).  .
.
5. Investigate the function for continuity:  .
.
Module 2. Analitic geometry. Introduction to Calculus
Individual Home Task
Variant 4
1. For the triangle with the vertices А (-5;-2), В (7;6), С (5;-4) find:
a) length of the side АВ;
b) equation of the line АМ which parallel to the side ВС;
c) the equation of the hieght ВF;
d) the equation of the median AD;
e) the interior angle  ;
;
f) the coordinates of the points N and K, which divides the greater sige of the triangular into three equal parts;
g) area of the treangular АВС.
3. There are given the points М 1(1;-2;-4), M 2(2;–1;3), of the plane Р 1: 5x+3y-4z+8=0,
Р 2: x-y+z+5=0 and лінії L 1: 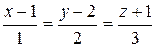 ; L 2:
; L 2: 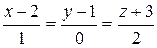 .
.
а) Write down the equation of the straight line passing through the points М 1 and M 2;
b) Find the acute angle between the lines L 1 and L 2;
c) Through the point M 2 draw the plane parallel to the plane Р 2;
d) Find the acute angle between the planes Р 1 and Р 2;
e) Find the distance from the point М 1 to the plane Р 2;
f) Through the point M 2 draw the line parallel to the line L 2;
g) Find the acute angle between the line L 2 and the plane Р 2;
h) Through the point М 1 draw the line perpendicular to the plane Р 1;
i) Write down the equation of the plane passing through the point М 1 and perpendicular to the planes Р 1 and Р 2;
j) Write down the canonic equation of the line which is the concurent of two planes Р 1 and Р 2.
3. Calculate the limits: а) 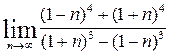 ; b)
; b)  ;
;
c)  ; d)
; d) 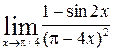 .
.
4. Calculate the limits: а) 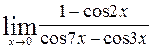 ; b)
; b) 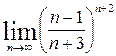 .
.
5. Investigate the function for continuity: 
Дата добавления: 2015-10-28; просмотров: 127 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Module 2. Analitic geometry. Introduction to Calculus | | | Module 2. Analitic geometry. Introduction to Calculus |