Module 2. Analitic geometry. Introduction to Calculus. Module 2. Analitic geometry

Module 2. Analitic geometry. Introduction to Calculus

Individual Home Task

Variant 1

1. For the triangle with the vertices А (-3;5), В (11;-12), С (-7;12) find:

a) length of the side АВ;

b) equation of the line АМ which parallel to the side ВС;

c) the equation of the hieght ВF;

d) the equation of the median AD;

e) the interior angle ;

f) the coordinates of the points N and K, which divides the greater sige of the triangular into three equal parts;

g) area of the treangular АВС.

2. There are given the points М ₁(3;-1;2), M ₂(2;4;-2), planes Р ₁: 2x+3y-4z+5=0,
Р ₂: x-y+z+2=0 and lines L ₁: ; L ₂: .

а) Write down the equation of the straight line passing through the points М ₁ і M ₂;

b) Find the acute angle between the lines L ₁ і L ₂;

c) Through the point M ₂ draw the plane parallel to the plane Р ₂;

d) Find the acute angle between the planes Р ₁ і Р ₂;

e) Find the distance from the point М ₁ to the plane Р ₂;

f) Through the point M ₂ draw the line parallel to the line L ₂;

g) Find the acute angle between the line L ₂ and the plane Р ₂;

h) Through the point М ₁ draw the line perpendicular to the plane Р ₁;

i) Write down the equation of the plane passing through the point М ₁ and perpendicular to the planes Р ₁ and Р ₂;

j) Write down the canonic equation of the line which is the concurent of two planes Р ₁ and Р ₂.

3. Calculate the limits: а) 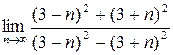; b) ;

c) ; d) .

4. Calculate the limits: а) ; b). .

5. Investigate the function for continuity: .

Module 2. Analitic geometry. Introduction to Calculus

Individual Home Task

Variant 2

1. For the triangle with the vertices А (-3;4), В (-4;-3), С (8;1) find:

a) length of the side АВ;

b) equation of the line АМ which parallel to the side ВС;

c) the equation of the hieght ВF;

d) the equation of the median AD;

e) the interior angle ;

f) the coordinates of the points N and K, which divides the greater sige of the triangular into three equal parts;

g) area of the treangular АВС.

2. There are given the points М ₁(3;1;–4), M ₂(1;–3;2), of the plane Р ₁: 2 x – y – z + 4=0,
Р ₂: x -4 y +5 z -1=0 and lines L ₁: ; L ₂: .

а) Write down the equation of the straight line passing through the points М ₁ and M ₂;

b) Find the acute angle between the lines L ₁ and L ₂;

c) Through the point M ₂ draw the plane parallel to the plane Р ₂;

d) Find the acute angle between the planes Р ₁ and Р ₂;

e) Find the distance from the point М ₁ to the plane Р ₂;

f) Through the point M ₂ draw the line parallel to the line L ₂;

g) Find the acute angle between the line L ₂ and the plane Р ₂;

h) Through the point М ₁ draw the line perpendicular to the plane Р ₁;

i) Write down the equation of the plane passing through the point М ₁ and perpendicular to the planes Р ₁ and Р ₂;

j) Write down the canonic equation of the line which is the concurent of two planes Р ₁ and Р ₂.

3. Calculate the limits: а) 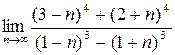; b) ;

c) ; d) .

4. Calculate the limits: а) 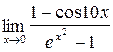; b) .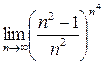

5. Investigate the function for continuity.

Module 2. Analitic geometry. Introduction to Calculus

Дата добавления: 2015-10-28