Раздел №1. Моделирование геометрических операций и фигур

ПРАКТИКУМ по Microsoft Paint

Задача 1.1 Моделирование геометрических операций.

Модель 1. Деление отрезков (моделирование функций линейки)

Алгоритм деления отрезка пополам приведен на рисунке 1.1. Построение основано на том, что высота в равнобедренном треугольнике является одновременно биссектрисой и медианой. Для построения достаточно инструмента Линия и клавиши Shift.

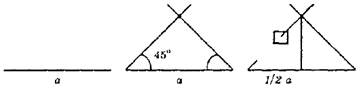
Рис. 1.1. Алгоритм деления отрезка пополам

Алгоритм деления отрезка на n равных частей (для n =3) приведен на рисунке 1.2. Для выполнения операции деления используется отрезок произвольной длины х. Построение основано на подобии треугольников. Параллельность линий достигается копированием.

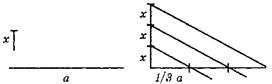
Рис. 1.2. Алгоритм деления отрезка на n равных частей

Модель 2. Построение окружности заданного радиуса и определение ее центра (моделирование функций циркуля)

Окружность в графическом редакторе вписывается в квадрат со стороной, равной удвоенному радиусу. Алгоритм построения окружности изображен на рисунке 1.3.

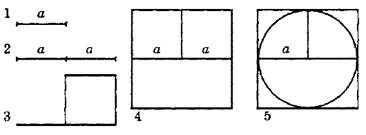
Рис. 1.3. Алгоритм построения окружности с заданным радиусом

Модель 3. Деление угла пополам (моделирование функции транспортира)

На рисунке 1.4 приведен один из вариантов алгоритма деления. 

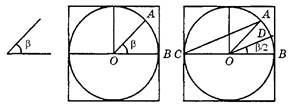
Рис. 1.4. Алгоритм деления угла пополам

В качестве дополнительного построения используется окружность любого радиуса. В ее центр помещается копия угла, подлежащего делению. Углы АОВ и АСВ относятся как 2:1 (докажите это). Отсюда, если линия DO параллельна линии АС, то она является биссектрисой заданного угла. Построение сводится к копированию части отрезка АС и установке его копии к точке О. Полученная параллельная линия DO разделит заданный угол пополам.

Задача 1.2 Моделирование объектов с заданными геометрическими свойствами.

Модель 4. Построение равностороннего треугольника с заданной стороной

Данный алгоритм предложил Евклид в IV в. до н. э. Построить треугольник по алгоритму, приведенному на рисунке 1.5, и доказать, что полученный треугольник действительно правильный.

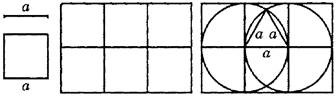
Рис. 1.5. Алгоритм построения равностороннего треугольника с заданной стороной

Модель 5. Построение правильного шестиугольника с заданной стороной

Используя свойство правильных фигур вписываться в окружность и то, что сторона равностороннего шестиугольника равна радиусу описанной окружности, выполнить построение по алгоритму на рисунке 1.6. Начать построение окружности с радиусом, равным заданной стороне шестиугольника.

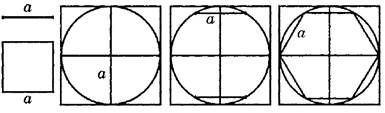
Рис. 1.6. Алгоритм построения правильного шестиугольника с заданной стороной

Дата добавления: 2015-10-26