L’espace et le temps

Nos idйes actuelles sur le mouvement des corps datent de Galilйe et de Newton. Avant eux, les hommes croyaient Aristote, lorsque ce dernier avanзait que l’йtat naturel d’un corps йtait d’кtre au repos et qu’il ne se dйplaзait que sous l’action d’une force ou d’une poussйe. Il s’ensuivait qu’un corps lourd devait tomber plus vite qu’un corps lйger, parce qu’il subissait une plus grande attirance vers la Terre.

La tradition aristotйlicienne soutenait йgalement que l’on pouvait trouver toutes les lois qui rйgissent l’univers par la seule rйflexion: vйrifier par l’observation n’йtait pas nйcessaire. Aussi, personne jusqu’а Galilйe ne s’йtait-il donnй la peine de voir si des corps de poids diffйrents tombaient vraiment selon des vitesses diffйrentes. On dit que Galilйe montra qu’Aristote se trompait en laissant tomber des poids du haut de la tour penchйe de Pise. L’histoire est presque certainement inexacte et Galilйe a dы faire quelque chose comme laisser rouler des billes de poids diffйrents sur une pente douce. La situation est semblable а celle de corps pesants tombant а la verticale, mais elle est plus facile а observer parce que les vitesses sont plus faibles. Les mesures de Galilйe montrиrent que chaque corps voit sa vitesse augmenter dans la mкme proportion, quel que soit son poids. Si vous laissez courir une bille sur une pente qui descend de 1 mиtre tous les 10 mиtres, la bille effectuera sa descente а la vitesse de 1 mиtre par seconde aprиs 1 seconde, 2 mиtres par seconde aprиs 2 secondes, et ainsi de suite, quel que soit le poids de la bille. Bien sыr, un poids supйrieur tombe plus vite qu’un poids moindre, mais c’est uniquement parce qu’un poids lйger est ralenti par la rйsistance de l’air. Si on laisse tomber deux corps de poids diffйrents qui ne prйsentent pas grande rйsistance а l’air, ils tomberont а la mкme vitesse.

Les mesures de Galilйe furent utilisйes par Newton comme base de ses lois du mouvement. Dans les expйriences de Galilйe, un corps roulant sur une pente est toujours soumis а la mкme force (son poids) dont l’effet augmenterait constamment sa vitesse. Cela montre que la vйritable action d’une force est toujours de modifier la vitesse d’un corps, au lieu de mettre simplement celui-ci en mouvement, comme on le pensait prйcйdemment. Cela signifie aussi que lorsqu’un corps n’est soumis а aucune force, il continue а se dйplacer en ligne droite а la mкme vitesse. Cette notion fut pour la premiиre fois explicitйe dans les Principia Mathematica de Newton, publiйs en 1687, et elle est connue sous le nom de «premiиre loi de Newton». Ce qui arrive а un corps lorsqu’une force agit sur lui est йnoncй par la «seconde loi de Newton»: le corps accйlйrera (sa vitesse sera modifiйe continыment) proportionnellement а l’intensitй de la force. (Exemple: pour une force deux fois plus grande, l’accйlйration sera deux fois plus grande.) L’accйlйration sera aussi plus faible si la masse du corps (quantitй de matiиre) est plus grande. (La mкme force agissant sur un corps de masse deux fois plus grande produira la moitiй de l’accйlйration.) Un exemple bien connu est celui d’une voiture: plus le moteur est puissant, plus l’accйlйration est grande, mais plus la voiture est lourde, plus l’accйlйration sera faible pour un mкme moteur.

En plus des lois du mouvement, Newton dйcouvrit la loi de la force de gravitй: tout corps attire tout autre corps selon une force proportionnelle а la masse de chacun des corps. Ainsi, la force agissant entre deux corps A et B devrait кtre deux fois plus forte si l’un des corps (disons le corps A) avait une masse double. C’est ce а quoi vous pourriez vous attendre, parce que l’on pourrait penser que le nouveau corps A est en fait constituй de deux corps ayant chacun la masse d’origine et attirant chacun le corps B selon la force d’origine. Donc, la force totale entre A et B devrait кtre le double de la force d’origine. Et si l’un des corps avait une masse double, et l’autre, une masse triple de celle de dйpart, alors la force qui les attirerait serait six fois plus forte. On voit maintenant pourquoi tous les corps tombent а la mкme vitesse: un corps ayant deux fois un poids donnй subira une force de gravitй le poussant doublement vers le bas, mais il aura aussi une masse double. Selon la seconde loi de Newton, ces deux effets s’annuleront exactement l’un l’autre, si bien que l’accйlйration sera la mкme dans tous les cas.

La loi de la gravitation de Newton nous dit йgalement que plus les corps seront йloignйs les uns des autres, plus la force d’attraction sera faible. Elle dit encore que l’attraction gravitationnelle d’une йtoile sur un corps est exactement le quart de celle d’une йtoile similaire qui serait situйe а mi-distance de ce corps. Elle prйdit les orbites de la Terre, de la Lune et des planиtes avec une grande exactitude. Si elle avait stipulй que l’attraction gravitationnelle d’une йtoile diminue plus rapidement avec la distance, les orbites des planиtes n’auraient pas йtй elliptiques, elles auraient йtй des spirales aboutissant au Soleil. Si elle avait diminuй plus lentement, les forces gravitationnelles venant des йtoiles йloignйes auraient dominй celle venant de la Terre.

La grande diffйrence entre les idйes d’Aristote et celles de Galilйe et de Newton est qu’Aristote croyait en un йtat prйfйrentiel de repos que chaque corps adopterait s’il n’йtait soumis а aucune force ou а aucune poussйe. En particulier, il pensait que la Terre йtait au repos. Mais il dйcoule des lois de Newton qu’il n’y a pas de norme unique de repos. On pourrait aussi bien dire que le corps A est au repos et que le corps B se dйplace а vitesse constante relativement au corps A, ou que le corps B est au repos et que c’est A qui se dйplace. Par exemple, si l’on fait un moment abstraction de la rotation de la Terre et de son orbite autour du Soleil, on peut tout aussi bien dire que la Terre est au repos et que le train а sa surface se dirige vers le nord а cent cinquante kilomиtres а l’heure, ou que c’est le train qui est au repos et la Terre qui se dйplace vers le sud а cent cinquante kilomиtres а l’heure. Si l’on avait fait des expйriences dans ce train sur la chute des corps, toutes les lois de Newton auraient йtй conservйes. Par exemple, en y jouant au ping-pong, on aurait trouvй que la balle obйissait aux lois de Newton exactement comme une balle sur une table qui aurait йtй installйe sur la voie. Aussi n’y a-t-il aucun moyen de dire qui, du train ou de la Terre, est en mouvement.

L’absence de norme absolue de repos signifie que l’on ne peut dйterminer si deux йvйnements qui ont eu lieu а deux moments diffйrents sont advenus dans la mкme position dans l’espace. Par exemple, supposons que notre balle de ping-pong dans le train rebondisse а la verticale, heurtant la table au mкme endroit а une seconde d’intervalle. Pour quelqu’un sur la voie, les deux rebonds sembleraient s’effectuer а une centaine de mиtres l’un de l’autre parce que le train aurait avancй sur ses rails entre-temps. La non-existence du repos absolu signifie donc que l’on ne peut donner а un йvйnement une position absolue dans l’espace, comme le croyait Aristote. La localisation des йvйnements et la distance entre eux diffйreraient donc pour une personne dans le train de celles йvaluйes par une autre sur la voie, et il n’y aurait aucune raison a priori de «prйfйrer» la position de l’une plutфt que celle de l’autre.

Newton йtait trиs chagrinй par cette absence de localisation absolue, ou d’espace absolu, comme on disait, parce que cela ne s’accordait pas avec sa notion d’un Dieu absolu. En fait, il refusa de l’admettre bien que cela fыt sous-entendu par ses lois. Il fut sйvиrement critiquй pour cette croyance irrationnelle par beaucoup de gens et plus particuliиrement par l’йvкque Berkeley, un philosophe qui pensait que tous les objets matйriels, l’espace et le temps sont une illusion. Quand le cйlиbre Dr Johnson fut informй de l’opinion de Berkeley, il s’йcria: «Je la rйfute donc!» et il heurta une grosse pierre du pied.

Aristote et Newton croyaient tous deux en un temps absolu. C’est-а-dire qu’ils pensaient que l’on pouvait mesurer sans ambiguпtй l’intervalle de temps sйparant deux йvйnements et que cet intervalle serait le mкme quelle que soit la personne qui le mesure, pourvu que l’on se serve d’une bonne horloge. Le temps йtait encore complиtement sйparй et indйpendant de l’espace. C’est ce que la plupart des gens considйreraient encore aujourd’hui comme une opinion sensйe. Pourtant nous avons йtй amenйs а modifier nos idйes sur l’espace et le temps. Bien que ces notions qui nous semblent justes fonctionnent lorsqu’il s’agit de pommes ou de planиtes qui se meuvent relativement lentement, elles ne sont plus du tout valables dans le cas d’objets se dйplaзant а la vitesse de la lumiиre ou presque.

La lumiиre voyage а une vitesse finie, mais trиs йlevйe; cela a йtй dйcouvert pour la premiиre fois en 1676 par l’astronome danois Ole Christensen Rњmer. Celui-ci observa que les disparitions des lunes de Jupiter derriиre cette planиte n’йtaient pas йgalement espacйes dans le temps, comme on aurait pu s’y attendre si les lunes avaient orbitй а vitesse constante. Comme la Terre et Jupiter tournent autour du Soleil, la distance entre les deux planиtes varie. Rњmer remarqua que les йclipses des lunes de Jupiter йtaient d’autant plus tardives que nous йtions plus loin de la planиte gйante. Il affirma que c’йtait parce que la lumiиre de ses lunes mettait plus longtemps а nous atteindre quand nous en йtions plus йloignйs. Les mesures des variations de distance entre la Terre et Jupiter dont il disposait n’йtant pas trиs exactes, il avanзa pour la vitesse de la lumiиre deux cent mille kilomиtres par seconde environ alors que la valeur moderne est de trois cent mille kilomиtres par seconde. Nйanmoins, son exploit – non seulement Rњmer prouvait que la lumiиre voyageait а une vitesse finie, mais encore avait-il mesurй cette vitesse – йtait remarquable, intervenant, comme ce fut le cas, onze ans avant la publication par Newton des Principia Mathematica.

Une vйritable thйorie de la propagation de la lumiиre ne fut йlaborйe qu’en 1865, quand le physicien britannique James Clerk Maxwell rйussit а unifier les thйories partielles qui jusqu’alors avaient йtй utilisйes pour dйcrire les forces de l’йlectricitй et du magnйtisme. Les йquations de Maxwell prйdisaient qu’il pourrait y avoir des perturbations en forme d’onde dans le champ combinй йlectromagnйtique, et que ces derniиres se propageraient а une vitesse donnйe, comme des rides а la surface d’un йtang. Si la longueur d’onde de ces ondes (distance entre la crкte d’une onde et la suivante) est d’un mиtre ou plus, il s’agit de ce que nous appelons maintenant des ondes radio. Des longueurs d’onde plus courtes sont connues sous le nom d’ondes centimйtriques (quelques centimиtres) ou encore infrarouges (plus d’un dix milliиme de centimиtre). La lumiиre visible a une longueur d’onde comprise seulement entre quarante et quatre-vingts millioniиmes de centimиtre. Les longueurs d’onde encore plus petites sont celles de l’ultraviolet, des rayons X et des rayons gamma.

La thйorie de Maxwell prйdisait que les ondes radio ou lumineuses se propageraient а une certaine vitesse, bien dйterminйe. Mais la thйorie de Newton s’йtait dйbarrassйe de la notion de repos absolu; donc, si la lumiиre йtait supposйe se propager а une vitesse donnйe, il faudrait prйciser relativement а quoi cette vitesse donnйe avait йtй mesurйe. On fit appel а une substance appelйe «йther», prйsente partout, mкme dans l’espace «vide». Les ondes lumineuses se propageraient а travers l’йther comme les ondes sonores а travers l’air, et leur vitesse serait donc relative а ce milieu. Diffйrents observateurs, en mouvement par rapport а l’йther, verraient donc la lumiиre arriver dans leur direction а des vitesses diffйrentes, mais la vitesse de la lumiиre par rapport а l’йther resterait fixe. En particulier, comme la Terre est en mouvement dans l’йther sur son orbite autour du Soleil, la vitesse de la lumiиre mesurйe dans la direction du mouvement de la Terre dans l’йther (lorsque nous nous dйplaзons en direction de la source de lumiиre) devrait кtre plus йlevйe que la vitesse de la lumiиre perpendiculaire а ce mouvement (lorsque nous ne nous dйplaзons pas vers la source lumineuse). En 1887, Albert Michelson (qui par la suite devait кtre le premier Amйricain а recevoir le prix Nobel de physique) et Edward Morley firent une expйrience trиs minutieuse а la Case School of Applied Science а Cleveland. Ils comparиrent la vitesse de la lumiиre dans la direction du mouvement de la Terre et perpendiculairement а ce mouvement. А leur grande surprise, ils trouvиrent deux valeurs exactement identiques!

Entre 1887 et 1905, il y eut plusieurs tentatives, en particulier celle du physicien hollandais Hendrick Lorentz, pour expliquer les rйsultats de l’expйrience de Michelson-Morley en termes d’objets contractйs et d’horloges ralentissant en voyageant а travers l’йther. Cependant, dans un article cйlиbre paru en 1905, un employй jusque-lа inconnu du Bureau des brevets en Suisse, Albert Einstein, fit remarquer que toute idйe d’йther йtait inutile pourvu que l’on veuille bien abandonner l’idйe de temps absolu. Une remarque semblable fut faite quelques semaines plus tard par un grand mathйmaticien franзais, Henri Poincarй. Les arguments d’Einstein йtant de nature plus physique que ceux de Poincarй – qui avait abordй le problиme en mathйmaticien –, Einstein est habituellement crйditй de la nouvelle thйorie, mais on doit se souvenir de Poincarй comme d’un nom attachй а une partie importante de cette thйorie.

Le postulat fondamental de la thйorie de la Relativitй, comme on l’appela, c’est que les lois de la physique devraient кtre les mкmes pour tous les observateurs se mouvant librement, quelle que soit leur vitesse. C’йtait vrai pour les lois newtoniennes du mouvement, mais maintenant, cette idйe йtait йtendue jusqu’а inclure la thйorie de Maxwell et la vitesse de la lumiиre: tous les observateurs devraient mesurer la mкme vitesse pour la lumiиre, quelle que soit la vitesse de leur dйplacement. Cette notion simple a quelques consйquences remarquables. Peut-кtre les plus connues sont-elles l’йquivalence de la masse et de l’йnergie, rйsumйe dans la cйlиbre йquation d’Einstein E = mcІ (oщ E est l’йnergie, m la masse et c la vitesse de la lumiиre), et la loi voulant que rien ne peut se dйplacer plus vite que la lumiиre. Par suite de l’йquivalence entre йnergie et masse, l’йnergie qu’un objet possиde en raison de son mouvement augmentera sa masse et, par consйquent, il lui deviendra encore plus difficile d’augmenter sa vitesse. Cet effet n’est rйellement significatif que pour des objets se dйplaзant а des vitesses proches de celle de la lumiиre. Par exemple, а 10 % de la vitesse de la lumiиre, la masse d’un objet n’est que de 0,5 % supйrieure а l’ordinaire, alors qu’а 90 % de la vitesse de la lumiиre, l’objet verra sa masse plus que multipliйe par deux. S’il approche la vitesse de la lumiиre, sa masse augmentera toujours plus vite, de telle sorte que cela lui demandera de plus en plus d’йnergie pour aller toujours plus vite. Il ne pourra en fait jamais atteindre la vitesse de la lumiиre, parce que alors sa masse devrait кtre infinie, et qu’en raison de l’йquivalence entre sa masse et son йnergie, cela lui demanderait une quantitй infinie d’йnergie pour y arriver. C’est ainsi que tout objet normal en est а tout jamais rйduit par la Relativitй а se mouvoir а des vitesses infйrieures а celle de la lumiиre. Seule la lumiиre, ou d’autres phйnomиnes dйnuйs de masse intrinsиque, peuvent l’atteindre.

Autre consйquence remarquable de la Relativitй: la rйvolution qu’elle a semйe dans nos idйes sur l’espace et le temps. Dans la thйorie de Newton, si un йclair lumineux est envoyй d’un endroit а un autre, diffйrents observateurs seront d’accord sur le temps que le voyage aura pris (йtant donnй que le temps est absolu), mais ne seront pas toujours d’accord sur la distance que la lumiиre aura parcourue (йtant donnй que l’espace n’est pas absolu). Comme la vitesse de la lumiиre n’est que la distance qu’elle a parcourue divisйe par le temps qu’elle a mis pour le faire, des observateurs diffйrents devraient mesurer des vitesses diffйrentes pour la lumiиre. En Relativitй, au contraire, tous les observateurs sont d’accord sur la vitesse de la lumiиre. Ils ne sont cependant pas d’accord sur la distance parcourue, aussi doivent-ils йgalement кtre en dйsaccord sur la durйe du trajet. (Cette durйe n’est, aprиs tout, que la distance que la lumiиre a parcourue – sur laquelle les observateurs ne sont pas d’accord – divisйe par la vitesse de la lumiиre – sur laquelle ils sont d’accord.) En d’autres termes, la thйorie de la Relativitй a mis un terme а l’idйe de temps absolu! Il est alors apparu que chaque observateur devrait avoir sa propre mesure de temps, effectuйe par une horloge qu’il emporterait avec lui, et que des horloges identiques, aux mains d’observateurs diffйrents, ne devraient pas nйcessairement indiquer la mкme chose.

Chaque observateur devrait utiliser un йmetteur pour dire oщ et quand un йvйnement a lieu en envoyant un йclair lumineux ou des ondes radio. Une partie de l’йclat sera renvoyйe а l’йvйnement et l’observateur mesurera le temps mis pour recevoir cet йcho. Le temps de l’йvйnement est alors rйputй кtre la moitiй de celui qui s’est йcoulй entre le moment oщ l’йclair a йtй envoyй et celui oщ sa rйflexion a йtй reзue; la distance de l’йvйnement est la moitiй du temps pris pour ce voyage aller-retour, multipliйe par la vitesse de la lumiиre. (Un йvйnement, dans ce sens, est quelque chose qui a lieu en un point unique de l’espace, а un instant prйcis dans le temps.) Cette idйe est illustrйe sur la fig. 2.1, exemple de diagramme espace-temps. En utilisant cette procйdure, les observateurs qui se dйplacent relativement les uns par rapport aux autres assigneront des temps et des positions diffйrents au mкme йvйnement. Aucune mesure d’un observateur particulier ne sera plus correcte qu’une autre, mais toutes les mesures seront relatives. Tout observateur peut trouver prйcisйment le temps et la position que tout autre observateur assignera а un йvйnement, pourvu qu’il connaisse sa vitesse relative.

Figure 2.1

De nos jours, nous utilisons cette mйthode pour mesurer les distances avec exactitude, parce que nous pouvons mesurer le temps plus exactement que la longueur. En effet, le mиtre est dйfini comme la distance parcourue par la lumiиre en 0,000000003335640952 seconde, mesurйe par une horloge au cйsium. (La raison de ce nombre particulier est qu’il correspond а la dйfinition historique du mиtre, deux marques sur une barre de platine conservйe а Paris.) De faзon йquivalente, nous pouvons utiliser une nouvelle unitй de longueur plus pratique, que l’on appelle la seconde-lumiиre. On la dйfinit absolument comme la distance que la lumiиre parcourt en 1 seconde. Dans la thйorie de la Relativitй, nous dйfinissons maintenant les distances en termes de temps et de vitesse de la lumiиre, d’oщ il s’ensuit automatiquement que chaque observateur mesurera la mкme vitesse de la lumiиre (par dйfinition, 1 mиtre par 0,000000003335640952 seconde). Nul besoin d’introduire l’idйe d’un йther, dont la prйsence de toute faзon n’a pas йtй dйtectйe, comme l’expйrience de Michelson-Morley l’a montrй. La thйorie de la Relativitй, cependant, nous force а modifier fondamentalement nos idйes sur l’espace et le temps. Nous devons accepter que le temps ne soit pas complиtement sйparй de l’espace ni indйpendant de lui, mais qu’il se combine а lui pour former un objet appelй «espace-temps».

On sait que l’on peut dйcrire la position d’un point dans l’espace grвce а trois nombres, ses coordonnйes. Par exemple, on peut dire qu’un point dans une piиce est а 2 mиtres d’un mur, 1 mиtre d’un autre et а 1,50 mиtre au-dessus du plancher. On pourrait aussi spйcifier qu’un point est а une certaine latitude, а une certaine longitude et а une certaine hauteur au-dessus du niveau de la mer. On est libre d’utiliser toutes coordonnйes adйquates, bien qu’elles n’aient qu’une portйe limitйe de validitй: on ne pourrait guиre spйcifier la position de la Lune en termes de kilomиtres au nord et а l’est de Piccadilly Circus et de pieds au-dessus du niveau de la mer. En revanche, il sera plus aisй de la dйfinir en termes de distance au Soleil, de distance au plan des orbites des planиtes et d’angle entre la droite joignant la Lune au Soleil et celle joignant le Soleil а une йtoile proche comme Alpha du Centaure. Ces coordonnйes elles-mкmes ne seraient pas non plus d’une grande utilitй pour dйcrire la position du Soleil dans notre Galaxie ou la position de notre Galaxie dans le Groupe Local. En fait, on peut dйcrire tout l’univers selon une collection de trames de rйfйrences se chevauchant. Sur chacune d’elles, on peut utiliser un ensemble diffйrent de trois coordonnйes pour spйcifier la position d’un point.

Un йvйnement est quelque chose qui arrive en un point particulier de l’espace а un moment particulier. Aussi peut-on le spйcifier par quatre nombres ou coordonnйes. Encore une fois, le choix des coordonnйes est arbitraire; on peut utiliser n’importe quelles coordonnйes spatiales bien dйfinies et n’importe quelle mesure du temps. En Relativitй, il n’y a pas de vйritable distinction entre l’espace et les coordonnйes de temps, tout comme il n’y a pas de vйritable diffйrence entre deux coordonnйes de l’espace. On pourrait choisir un nouvel ensemble de coordonnйes dans lequel la premiиre coordonnйe spatiale serait, mettons, la combinaison des anciennes premiиre et seconde coordonnйes. Par exemple, au lieu de mesurer la position d’un point sur la Terre en kilomиtres au nord et en kilomиtres а l’est de Piccadilly, on pourrait utiliser les kilomиtres au nord-est de Piccadilly et les kilomиtres au nord-ouest de Piccadilly. De la mкme faзon, en Relativitй, on pourrait utiliser une nouvelle coordonnйe de temps qui serait l’ancien temps (en secondes) plus la distance (en seconde-lumiиre) au nord de Piccadilly.

Il est souvent salutaire de penser aux quatre coordonnйes d’un йvйnement comme caractйrisant sa position dans un espace а quatre dimensions appelй espace-temps. Il est impossible d’imaginer un espace а quatre dimensions. Personnellement, je trouve dйjа difficile de visualiser l’espace а trois dimensions! Cependant, il est facile de tracer des diagrammes а deux dimensions, comme l’est la surface de la Terre. (On dit que la surface de la Terre est а deux dimensions parce que la position d’un point peut y кtre spйcifiйe par deux coordonnйes, latitude et longitude.) J’utiliserai gйnйralement des diagrammes dans lesquels le temps croоtra verticalement et oщ l’une des dimensions spatiales sera indiquйe horizontalement. Les deux autres dimensions spatiales seront nйgligйes ou, parfois, l’une d’elles sera indiquйe en perspective. (On les appelle des diagrammes d’espace-temps, comme sur la fig. 2.1.) Par exemple, sur la fig. 2.2, le temps est mesurй verticalement en annйes et la distance le long de la ligne allant du Soleil а Alpha du Centaure est mesurйe horizontalement en kilomиtres. Les trajets du Soleil et d’Alpha du Centaure а travers l’espace-temps apparaissent en lignes verticales, а droite et а gauche du diagramme. Un rayon de lumiиre venant du Soleil suit la diagonale et met quatre ans pour aller du Soleil а Alpha du Centaure.

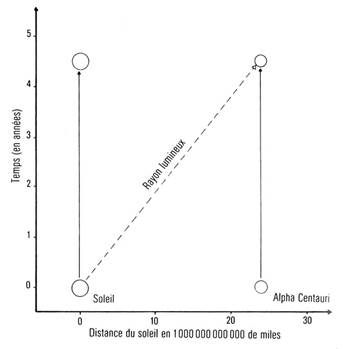
Figure 2.2

Comme nous l’avons vu, les йquations de Maxwell prйdisaient que la vitesse de la lumiиre devrait кtre la mкme quelle que soit la vitesse de la source, et cela a йtй confirmй par des mesures prйcises. Il s’ensuit que si un йclair de lumiиre est йmis а un instant particulier en un point particulier de l’espace, au fur et а mesure que le temps s’йcoulera, cet йclair grandira comme une sphиre de lumiиre dont la grandeur et la position seront indйpendantes de la vitesse de la source. Aprиs un millioniиme de seconde, la lumiиre se sera йtendue jusqu’а former une sphиre de trois cents mиtres de rayon; aprиs deux millioniиmes de seconde, ce rayon sera de six cents mиtres; et ainsi de suite, comme les rides qui s’йtendent а la surface d’un йtang quand un caillou y a йtй lancй. Les rides s’йtendent en un cercle qui s’йlargit au fur et а mesure que le temps passe. Si l’on pense а un modиle en trois dimensions constituй par la surface а deux dimensions de l’йtang et la dimension temps, le cercle en question formera un cфne dont le sommet sera situй а l’endroit et au moment oщ la pierre aura frappй l’eau (fig. 2.3). De faзon similaire, la lumiиre issue d’un йvйnement forme un cфne а trois dimensions dans l’espace-temps а quatre dimensions. Ce cфne est appelй le «cфne de lumiиre future» de l’йvйnement. De la mкme maniиre, nous pouvons dessiner un autre cфne, appelй le «cфne de lumiиre passйe», qui est l’ensemble des йvйnements d’oщ un йclair lumineux peut atteindre l’йvйnement en question (fig. 2.4).

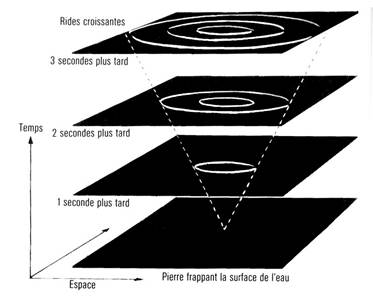
Figure 2.3

Figure 2.4

Les cфnes de lumiиre passйe et future d’un йvйnement P divisent l’espace-temps en trois rйgions (fig. 2.5).

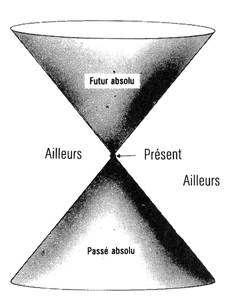
Figure 2.5

Le «futur absolu» de l’йvйnement est la rйgion intйrieure du cфne de lumiиre future de P. C’est l’ensemble de tous les йvйnements qui peuvent кtre influencйs par ce qui arrive en P. Les йvйnements hors du cфne de lumiиre de P ne peuvent кtre atteints par les signaux venant de P parce que rien ne peut voyager plus vite que la lumiиre. Donc, ils ne peuvent pas кtre affectйs par ce qui arrive en P. Le «passй absolu» de P est la rйgion а l’intйrieur du cфne de lumiиre passйe. C’est l’ensemble de tous les йvйnements d’oщ les signaux voyageant а la vitesse de la lumiиre ou presque peuvent atteindre P. C’est donc l’ensemble de tous les йvйnements qui peuvent affecter ce qui arrive en P. Si l’on connaоt ce qui arrive а tout instant particulier partout dans la rйgion de l’espace qui s’йtend а l’intйrieur du cфne de lumiиre passйe de P, on peut prйdire ce qui arrivera en P. «L’ailleurs» est la rйgion de l’espace-temps qui ne s’йtend dans aucun des cфnes de lumiиre – passйe ou future – de P. Les йvйnements dans «L’ailleurs» ne peuvent affecter les йvйnements en P, ni en кtre affectйs. Par exemple, si le Soleil devait cesser de briller а un instant prйcis, cela n’affecterait pas les choses sur la Terre au mкme moment parce que celle-ci serait dans Tailleurs de l’йvйnement Soleil-venant-de-s’йteindre (fig. 2.6). Nous ne saurions cela qu’aprиs huit minutes, temps que la lumiиre met а nous parvenir du Soleil. Ce n’est qu’а partir de lа que les йvйnements sur Terre s’йtendraient dans le cфne de lumiиre future de l’йvйnement qui aurait vu le Soleil s’йteindre; de faзon similaire, nous ne savons pas ce qui arrive en ce moment au loin dans l’univers: la lumiиre que nous captons en provenance des galaxies lointaines les a quittйes il y a quelque huit milliards d’annйes de cela. Aussi, lorsque nous regardons une rйgion de l’univers, la voyons-nous comme elle йtait dans le passй.

Figure 2.6

Si l’on nйglige les effets gravitationnels, comme le firent Einstein et Poincarй en 1905, on a ce que Ton appelle la thйorie de la Relativitй Restreinte. Pour chaque йvйnement dans L’espace-temps, nous pouvons construire un cфne de lumiиre (l’ensemble de tous les rayons lumineux dans L’espace-temps йmissibles а cet instant); et puisque la vitesse de la lumiиre est la mкme а chaque йvйnement et dans toutes les directions, tous les cфnes de lumiиre seront identiques et iront tous dans la mкme direction. La thйorie nous dit aussi que rien ne peut voyager plus vite que la lumiиre. Cela signifie que la trajectoire de tout objet а travers l’espace et le temps peut кtre reprйsentйe par une droite qui s’йtend а l’intйrieur du cфne de lumiиre pour tout йvйnement figurant sur cette droite (fig. 2.7).

Figure 2.7

La thйorie de la Relativitй Restreinte expliqua de faзon trиs efficace le fait que la vitesse de la lumiиre apparaisse la mкme а tous les observateurs (comme l’a prouvй l’expйrience de Michelson-Morley) et ce qui arrive lorsque les choses se meuvent а des vitesses proches de celle de la lumiиre. Cependant, elle йtait incompatible avec la thйorie newtonienne de la gravitation, qui disait que les objets s’attirent les uns les autres selon une force qui dйpend de la distance qui les sйpare. Cela signifiait que si l’on changeait de place l’un des objets, la force exercйe sur l’autre serait instantanйment modifiйe. Ou, en d’autres termes, que les effets gravitationnels devraient voyager а une vitesse infinie, et non а une vitesse йgale ou infйrieure а celle de la lumiиre, comme la thйorie de la Relativitй Restreinte l’exigeait; Einstein fit nombre d’essais infructueux entre 1908 et 1914 pour trouver une thйorie de la gravitation qui soit compatible avec la Relativitй Restreinte. Finalement, en 1915, il proposa ce que nous appelons maintenant la thйorie de la Relativitй Gйnйrale.

Einstein avanзa la suggestion rйvolutionnaire que la gravitation n’йtait pas une force comme les autres, mais une consйquence du fait que l’espace-temps n’est pas plat, ce qui avait dйjа йtй envisagй: il est courbe, ou «gauchi» par la distribution de masse et d’йnergie qu’il contient. Des corps comme la Terre ne sont pas obligйs de se mouvoir sur des orbites courbes а cause d’une force appelйe gravitation; ils suivent en fait ce qui se rapproche le plus d’une trajectoire rectiligne dans un espace courbe, c’est-а-dire une gйodйsique. Une gйodйsique est la plus courte (ou la plus longue) trajectoire entre deux points voisins. Par exemple, la surface de la Terre est un espace courbe а deux dimensions. Une gйodйsique sur la Terre est appelйe un grand cercle et c’est le plus court chemin entre deux points (fig. 2.8). Comme la gйodйsique est la trajectoire la plus courte entre deux aйroports quelconques, c’est la route qu’un navigateur indiquera au pilote de l’avion. En Relativitй Gйnйrale, les corps suivent toujours des lignes droites dans un espace-temps а quatre dimensions, mais ils nous apparaissent nйanmoins se mouvoir le long de trajectoires courbes dans notre espace-temps а trois dimensions. (C’est un peu comme regarder un avion survoler un sol accidentй. Bien qu’il suive une ligne droite dans l’espace а trois dimensions, son ombre suit une trajectoire courbe sur le sol а deux dimensions.)

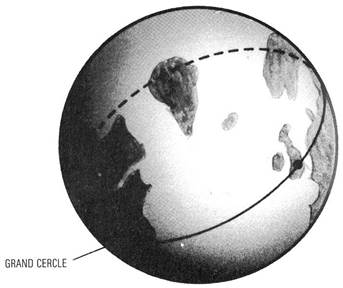
Figure 2.8

La masse du Soleil incurve l’espace-temps de telle sorte que, bien que la Terre suive une trajectoire droite dans un espace-temps а quatre dimensions, elle nous apparaоt comme se mouvant le long d’une orbite dans un espace а trois dimensions. En fait, les orbites des planиtes prйdites par la Relativitй Gйnйrale sont trиs exactement les mкmes que celles prйdites par la thйorie newtonienne de la gravitation. Cependant, dans le cas de Mercure, la planиte la plus proche du Soleil qui en ressent les effets gravitationnels le plus fortement et dont l’orbite est un peu plus allongйe, la Relativitй Gйnйrale prйdit que le grand axe de l’ellipse devrait tourner autour du Soleil au rythme d’environ un degrй tous les dix mille ans. Aussi petit que soit cet effet, il avait йtй remarquй avant 1915 et a йtй l’une des premiиres confirmations de la thйorie d’Einstein. Au cours des derniиres annйes, les dйviations encore plus faibles des autres planиtes par rapport aux prйdictions newtoniennes ont йtй mesurйes grвce au radar et sont en accord avec les prйdictions de la Relativitй Gйnйrale.

Les rayons lumineux aussi doivent suivre des gйodйsiques de l’espace-temps. Encore une fois, le fait que l’espace soit courbe signifie que la lumiиre ne peut plus apparaоtre dorйnavant comme voyageant en ligne droite dans l’espace. Ainsi, la Relativitй Gйnйrale prйdit-elle que la lumiиre devrait кtre dйviйe par les champs gravitationnels. La thйorie prйdit par exemple que les cфnes de lumiиre de points proches du Soleil sont lйgиrement incurvйs а cause de la masse du Soleil. Cela signifie que la lumiиre d’une йtoile lointaine qui passerait prиs du Soleil serait trиs lйgиrement dйviйe, ce qui fait que l’йtoile n’apparaоtrait pas au bon endroit pour un observateur sur Terre (fig. 2.9). Bien sыr, si la lumiиre venue de l’йtoile passait toujours prиs du Soleil, nous ne serions pas capables de dire si elle est dйviйe ou si l’йtoile se trouve rйellement lа oщ nous la voyons. Cependant, comme la Terre tourne autour du Soleil, des йtoiles diffйrentes ont l’occasion de passer derriиre lui et leur lumiиre d’кtre alors dйviйe. Elles changent donc de position apparente par rapport aux autres йtoiles.

Figure 2.9

Il est trиs difficile normalement de voir cet effet, parce que la lumiиre provenant du Soleil rend impossible l’observation d’йtoiles proches de lui dans le ciel. Cependant, il est possible de le dйtecter durant une йclipse de Soleil, lorsque la lumiиre de ce dernier est stoppйe par la Lune. La prйdiction d’Einstein sur la dйviation de la lumiиre ne put кtre immйdiatement vйrifiйe en 1915, а cause de la Premiиre Guerre mondiale; et ce n’est qu’en 1919 qu’une expйdition britannique, observant une йclipse en Afrique-Occidentale, en apporta la preuve. Cette confirmation d’une thйorie allemande par des savants anglais fut saluйe comme un grand acte de rйconciliation entre les deux pays. Il est donc assez drфle qu’un examen postйrieur des photographies prises lors de cette expйdition montre des erreurs aussi importantes que l’effet qu’elles йtaient censйes mesurer. Les mesures de l’йpoque dйcoulиrent de la chance pure et simple, et sont typiques du cas oщ l’on connaоt а l’avance le rйsultat que l’on veut obtenir; cela n’est pas si rare en science. La dйviation de la lumiиre a йtй, cependant, confirmйe avec exactitude par nombre d’observations ultйrieures.

Autre prйdiction de la Relativitй Gйnйrale: le temps devrait apparaоtre comme coulant moins vite prиs d’un corps massif comme la Terre. Cela а cause d’une relation entre l’йnergie de la lumiиre et sa frйquence (c’est-а-dire le nombre d’ondes de lumiиre par seconde): plus l’йnergie est grande, plus la frйquence est haute. Comme la lumiиre voyage vers le haut dans le champ gravitationnel de la Terre, elle perd de l’йnergie, et ainsi sa frйquence baisse. (Cela signifie que la longueur de l’intervalle de temps entre la crкte d’une onde et la suivante augmente.) Pour quelqu’un situй trиs au-dessus, il apparaоtrait que toute chose trиs en dessous prendrait plus de temps pour arriver. Cette prйdiction fut mise а l’йpreuve en 1962, а l’aide d’une paire d’horloges trиs exactes installйes au sommet et au pied d’une tour. On trouva que l’horloge du pied, qui йtait la plus proche de la Terre, marchait plus lentement, en accord exact avec la Relativitй Gйnйrale. La diffйrence de vitesse des horloges а diffйrentes hauteurs au-dessus de la Terre est de nos jours d’une importance pratique considйrable avec l’avиnement de systиmes de navigation trиs exacts basйs sur des signaux de satellites. Si l’on n’avait tenu aucun compte des prйdictions de la Relativitй Gйnйrale, les positions que l’on aurait ainsi calculйes auraient йtй fausses de plusieurs kilomиtres.

Les lois newtoniennes du mouvement ont mis fin а l’idйe de position absolue dans l’espace. La thйorie de la Relativitй s’est dйbarrassйe du temps absolu. Considйrons une paire de jumeaux. Supposons qu’un jumeau aille vivre au sommet d’une montagne pendant que l’autre reste au niveau de la mer. Le premier jumeau devrait vieillir plus vite que le second.

Donc, lorsqu’ils se rencontreront а nouveau, l’un devra кtre plus vieux que l’autre. Dans leur cas, la diffйrence d’вge serait minime, mais elle serait plus grande si l’un des jumeaux partait pour un long voyage dans un vaisseau spatial а une vitesse proche de celle de la lumiиre. А son retour, le voyageur devrait кtre beaucoup plus jeune que son frиre restй sur Terre. C’est ce que l’on appelle le «paradoxe des jumeaux», mais ce n’est un paradoxe que pour qui conserve une idйe de temps absolu derriиre la tкte. En Relativitй, il n’y a pas de temps absolu unique, chaque individu a sa propre mesure personnelle du temps qui dйpend du lieu oщ il est et de la maniиre dont il se dйplace.

Avant 1915, l’espace et le temps йtaient perзus comme une arиne figйe dans laquelle les йvйnements advenaient, elle-mкme n’йtant nullement affectйe par ce qu’il y advenait. C’йtait vrai mкme de la thйorie de la Relativitй Restreinte. Les corps se mouvaient, les forces attiraient et repoussaient, mais le temps et l’espace continuaient, tout simplement, sans altйration. Il йtait naturel de penser que l’espace et le temps coulaient а jamais.

La situation, cependant, est tout а fait diffйrente dans la thйorie de la Relativitй Gйnйrale. L’espace et le temps sont maintenant des quantitйs dynamiques: quand un corps se meut, ou quand une force agit, cela affecte la courbure de l’espace et du temps – et en retour, la structure de l’espace-temps affecte la faзon dont les corps se meuvent et dont les forces agissent. L’espace et le temps n’affectent pas seulement tout ce qui arrive dans l’univers, ils en sont aussi affectйs. Tout comme l’on ne peut parler d’йvйnement dans l’univers sans notions d’espace et de temps, il est devenu dйnuй de sens en Relativitй Gйnйrale de parler de l’espace et du temps hors des limites de l’univers.

Au cours de ces derniиres dйcennies, cette nouvelle comprйhension de l’espace et du temps a rйvolutionnй notre conception de l’univers. L’ancienne notion d’un univers fondamentalement sans changement, qui aurait existй et qui continuerait а exister, a йtй remplacйe pour toujours par la notion d’un univers dynamique, en expansion, qui semble avoir commencй il y a un temps fini, et qui pourrait se terminer а un instant donnй dans le futur. Cette rйvolution est le sujet du chapitre suivant. Et des annйes plus tard, cela devait кtre aussi le point de dйpart de mon travail en physique thйorique. Roger Penrose et moi-mкme avons montrй que la thйorie d’Einstein de la Relativitй Gйnйrale suggйrait que l’univers devait avoir un commencement et, peut-кtre, une fin.

Дата добавления: 2015-10-26