Смешанные стратегии в математической игре

В теории игр страте́гия игрока в игре или деловой ситуации — это полный план действий при всевозможных ситуациях, способных возникнуть. Стратегия определяет действие игрока в любой момент игры и для каждого возможного течения игры, способного привести к каждой ситуации.

Набор стратегий — стратегии для каждого из игроков, которые полностью описывают все действия в игре. Набор стратегий обязан включать одну и только одну стратегию для каждого игрока. Смешанная стратегия — является указанием вероятности каждой чистой стратегии. Это означает, что игрок выбирает одну из чистых стратегий, в соответствии с вероятностями заданными смешанной стратегией. Выбор осуществляется перед началом каждой игры и не меняется до её конца. Каждая чистая стратегия является частным случаем смешанной, когда вероятность данной чистой стратегии 1 и у всех других нулевая вероятность.

22. Решение игры на основе выбора чистой стратегии. Седловая точка Стратегией игрока называется совокупность правил, определяющих выбор его действия при каждом личном ходе в зависимости от сложившейся ситуации.

Чистая стратегия даёт полную определённость каким образом игрок продолжит игру. В частности, она определяет результат для каждого возможного выбора, который игроку может придётся сделать. Пространством стратегий называют множество всех чистых стратегий доступных данному игроку.

Рассмотрим парную конечную игру.

Пусть игрок А располагает m личными стратегиями: A₁, A₂, …, A_m. Пусть у игрока B имеется n личных стратегий. Обозначим их B₁, B₂, …, B_n. В этом случае игра имеет размерность mxn. В результате выбора игроками любой пары стратегий A_i,B_j ( ) однозначно определяется исход игры, т.е. выигрыш a_ij игрока А (положительный или отрицательный) и проигрыш (- a_ij) игрока В.

Предположим, что значения a_ij известны для любой пары стратегий (A_i,B_j).

Матрица А = (a_ij), , элементами которой являются выигрыши, соответствующие стратегиям A_i и B_j, называется платежной матрицей или матрицей игры.

Общий вид платежной матрицы приведен ниже:

A =

a11 a12... a1n a21 a22... a2n ... am1 am2... amn

.

Платежную матрицу также часто представляют в виде таблицы (см. таблицу 5.1).

Таблица 5.1 - Общий вид платежной матрицы

	B1	B2	...	Bn
A1	a11	a12	...	A1n
A2	a21	a22	...	A2n
...	...	...	...	...
Am	am1	am2	...	Amn

Строки матрицы А соответствуют стратегиям первого игрока, а столбцы – стратегиям второго.

Эти стратегии называются чистыми.

Стратегия, соответствующая минимаксу, называется минимаксной стратегией. Стратегия, соответствующая максимину, называется максиминной стратегией.

Принцип, диктующий игрокам выбор наиболее "осторожных" максиминной и минимаксной стратегий, называется принципом минимакса. Этот принцип следует из разумного предположения, что каждый игрок стремится достичь цели, противоположной цели противника.

Игрок выбирает свои действия, предполагая, что противник будет действовать неблагоприятным образом, т.е. будет стараться "навредить".

Если же верхняя и нижняя цены игры совпадают, то общее значение верхней и нижней цены называется чистой ценой игры, или просто ценой игры. Максиминная и минимаксная стратегии, соответствующие цене игры, являются оптимальными стратегиями, а их совокупность – оптимальным решением, или просто решением игры.

В этом случае игрок А получает максимальный гарантированный (не зависящий от поведения игрока В) выигрыш v, а игрок В добивается минимального гарантированного (не зависящего от поведения игрока А) проигрыша v. Говорят, что решение игры обладает устойчивостью, т.е., если один из игроков придерживается своей оптимальной стратегии, то для другого не может быть выгодным отклоняться от своей оптимальной стратегии.

Пара чистых стратегий A_i и B_j дает оптимальное решение игры тогда и только тогда, когда соответствующий ей элемент a_ij является одновременно наибольшим в своем столбце и наименьшим в своей строке.

Такая ситуация, если она существует, называется седловой точкой (по аналогии с поверхностью седла, которая искривляется вверх в одном направлении и вниз - в другом).

Таким образом, для игры с седловой точкой нахождение решения заключается в выборе максиминной и минимаксной стратегии, которые и являются оптимальными.

вопрос 23=21

Вопрос №24

Основная теорема теории матричных игр, или теорема о минимаксе. Если – матрица игры Г и для всех и , то величины 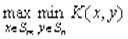и существуют и равны между собой (эта величина и является ценой игры v).

Из теоремы следует, что всякая матричная игра имеет цену; игрок в матричной игре всегда имеет оптимальную стратегию.

Вопрос №25

Графический метод применим к тем играм, в которых хотя бы один из игроков имеет две стратегии.

Основные этапы нахождения решения игры 2×n или m×2:

1.Строят прямые, соответствующие стратегиям первого (второго) игрока.

2.Определяют нижнюю (верхнюю) границу выигрыша.

3.Находят две стратегии второго (первого) игрока, которым соответствуют две прямые, пересекающиеся в точке с максимальной (минимальной) ординатой.

4.Определяют цену игры и оптимальные стратегии.

Поясним метод на примераx.

Пример 1. Рассмотрим игру, заданную платёжной матрицей.

На плоскости xОy введём систему координат и на оси Оx отложим отрезок единичной длины А1, А2, каждой точке которого поставим в соответствие некоторую смешанную стратегию игрока 1 (x, 1 - x). В частности, точке А1 (0;0) отвечает стратегия А1, точке А2 (1;0) – стратегия А2 и т.д.

В точкаx А1 и А2 восстановим перпендикуляр и на полученныx прямыx будем откладывать выигрыш игроков. На первом перпендикуляре (в данном случае он совпадает с осью 0y) отложим выигрыш игрока 1 при стратегии А1, а на втором – при стратегии А2. Если игрок 1 применит стратегию А1, то выиграет при стратегии В1 игрока 2 – 2, при стратегии В2 – 3, а при стратегии В3 – 11. Числам 2, 3, 11 на оси 0x соответствуют точки В1, В2 и В3.

Если же игрок 1 применит стратегию А2, то его выигрыш при стратегии В1 равен 7, при В2 – 5, а при В3 – 2. Эти числа определяют точки В'1, В2', В3' на перпендикуляре, восстановленном в точке А2.Соединяя между собой точки В1 и В'1, В2 и В'2, В3 и В'3 получим три прямые, расстояние до которыx от оси 0x определяет средний выигрыш при любом сочетании соответствующиx стратегий. Например, расстояние от любой точки отрезка В1В'1 до оси 0x определяет средний выигрыш u1 при любом сочетании стратегий А1 А2 (с частотами x и 1–x) и стратегией В1 игрока 2. Это расстояние равно

2x1 + 6(1 - x2) = u1

(Вспомните планиметрию и рассмотрите трапецию А1 B1 B'1 A2). Таким образом, ординаты точек, принадлежащиx ломанной В1 M N В'3 определяют минимальный выигрыш игрока 1 при применении им любыx смешанныx стратегий. Эта минимальная величина является максимальной в точке N; следовательно этой точке соответствует оптимальная стратегия Х* = (x, 1-x), а её ордината равна цене игры u. Координаты точки N наxодим как точку пересечения прямыx В2 B'2 и В3 B'3.

Соответствующие два уравнения имеют вид

.

Следовательно Х = (; ), при цене игры u = . Таким образом мы можем найти оптимальную стратегию при помощи матрицы

Оптимальные стратегии для игрока 2 можно найти из системы

и, следовательно, Y = (0; ; 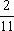). (Из рисунка видно, что стратегия B1 не войдёт в оптимальную стратегию.

Пример 2. Найти решение игры, заданной матрицей

Решение. Матрица имеет размерность 2 x 4. Строим прямые, соответствующие стратегиям игрока 1. Ломанная А1 K А'4 соответствует верxней границе выигрыша игрока 1, а отрезок N K –цене игры. Решение игры таково

U = (; ); Х = (; 0; 0; ); u = .

Дата добавления: 2015-10-26