Methods of processing the results of direct measurements containing random errors.

STATISTICAL REGULARITIES, ARISING OUT OF THE MEASUREMENT

PURPOSE:

Study the methods of processing the results of direct measurements.

INTRODUCTION:

It is impossible to do an experimental measurement with perfect accuracy. There is always an uncertainty associated with any measured quantity in an experiment even in the most carefully done experiment and despite using the most sophisticated instruments. This uncertainty in the measured value is known as the error in that particular measured quantity. There is no way by which one can measure a quantity with one hundred percent accuracy. In presenting experimental results it is very important to objectively estimate the error in the measured result. Such an exercise is very basic to experimental science.

THEORY

Measurement errors and their classification

Assume that the true value of a quantity is x₀. By measuring this value tend to get a result different from x₀. If the measurement is performed repeatedly, the measurement is not only different from x₀, but in most cases are different and each other. Denote measurements x₁, x₂, x₃,..., x_n, then the difference

Δ x_i = x_i - x₀, where i = 1, 2,..., n, (1)

is called the absolute error of measurement. It is expressed in units of the measured value.

In the classification of errors according to their properties distinguish systematic errors, random errors and misses.

Systematic errors in experimental observations usually come from the measuring instruments. They may occur because:

· there is something wrong with the instrument or its data handling system, or

· because the instrument is wrongly used by the experimenter.

Random errors in experimental measurements are caused by unknown and unpredictable changes in the experiment. These changes may occur in the measuring instruments or in the environmental conditions, for example: temperature, pressure, humidity.

Misses - a consequence of wrong actions of the experimenter. This, for example, incorrect recording of the results of observation, wrong metering, etc. If you notice misses they will be excluded from the calculations.

Methods of processing the results of direct measurements containing random errors.

Let at the same conditions done N measurements and x_i - the result of i-th dimension. The most probable value of the measured values ​​- its arithmetic mean value:

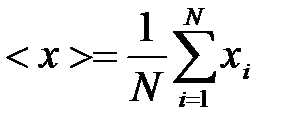(2)

The value of <x> tends to the true value x₀ of the measured value at N®¥. Mean square error of a single measurement result is the quantity

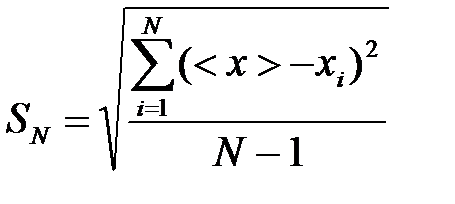(3)

When N®¥ S_N tends to the constant limit s:

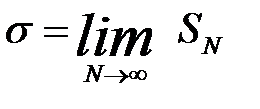(4)

The quantity s² called the dispersion of measurements.

Lets divide whole set of measurements at intervals. From all N measurements lets choose the minimum and maximum values ​​ x_min and x_max. The number of intervals K will be equal to the quotient of the division

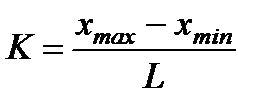
where L - step of interval.

Step of interval in this study should be an integer and chosen so that the number of intervals was not less than 8 and not more than 20. Intervals are numbered as follows:

1 – interval ,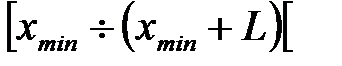

2 – interval ,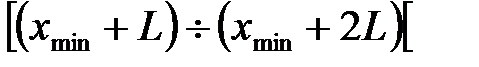

3 interval ,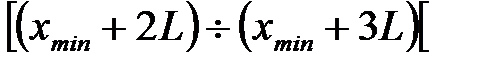

k – interval .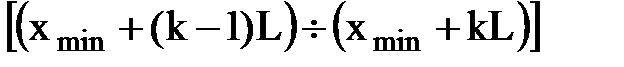

If on the abscissa the number of intervals will put aside, and on the ordinate- the number of measurements, whose results fall within this interval n_i, we get the empirical distribution graph of the measurements by intervals called histograms (Figure 1).

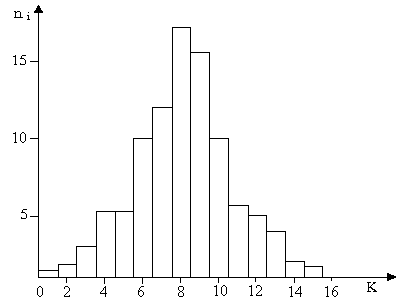
Figure 1. Distribution of the number of measurements at intervals (histogram)

At a large number of measurements the ratio n_i / N characterizes the probability of occurrence of values ​​of the measured values ​​in this interval with step L. If n_i/N divided by the step interval L, then the value will reflect the relative number of favorable cases to the unit interval. Diagram constructed for y_i, shows the distribution of the probability density at intervals and is called the reduced histogram. It has the form shown in Fig. 2.

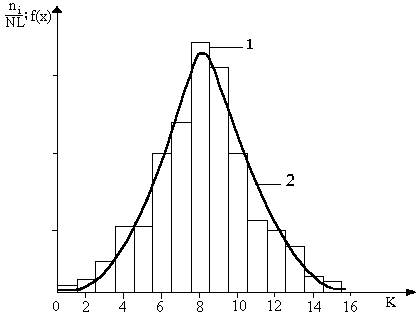
Fig. 2. Probability density distribution over the intervals: 1 - for a finite number of measurements (as specified histogram) and 2-Gauss curve

Now imagine that the measures continue so long as the number of measured values ​​becomes very large. Step interval L can be made very small (provided that the instrument has sufficient sensitivity), and yet in each interval will be many measurements.

In this case y_i can be viewed as a continuous function of x. Now, if instead of histogram plot the dependence y = f (x), which gives the fraction measurements of n_i, fall into the unit interval under a continuous variation of x, we obtain a smooth curve, called the distribution curve. The function y = f (x), respectively, called the density distribution. Its meaning is that the product f(x)dx (dx-differential of the independent variable) gives the fraction of the total number of measurements n_i / N, falling on the interval from x to x + dx. In other words, f(x)dx is the probability that an individual randomly selected value of the measured value will be in the range from x to x + dx.

The form of reduced histogram obtained for a small number of experiments can not be predicted in advance. But the theory of probability allows calculating the shape of the limiting form of the smooth curve, which tends to histograms with an indefinitely large number of experiments. This curve is called Gaussian curve (Figure 2).
Distribution corresponding to the limiting form of the curve is called a normal (Gaussian) distribution. It is described by a distribution function:

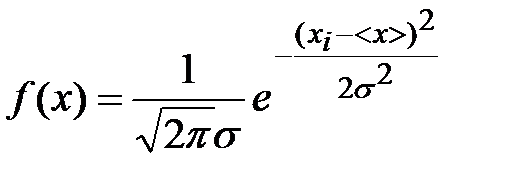, (5)

where 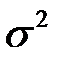- as already mentioned, is the dispersion, 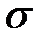characterizes the distribute of measurements about arithmetical mean value and is called the standard deviation or mean square error.

Gaussian function is normalized, i.e. f (x) satisfies the relation:

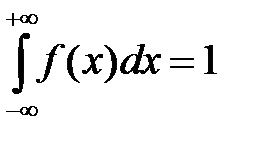. (6)

The integral has the infinite limits. This means that the measured value with probability 1 (or 100%) ranges from - ¥ to + ¥ or that the location of the measured value within these limits is a significant event. Probability density function has the following properties (see Fig. 2.):

· Symmetric with respect to <x>,

· reaches a maximum at <x>,

·
tends rapidly to zero as | x_i - <x>| becomes large compared with s

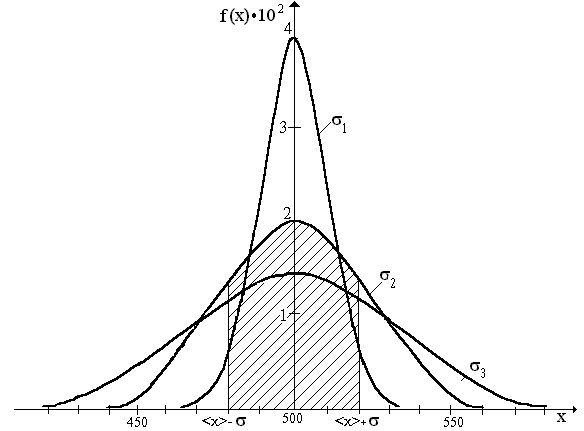
Fig. 3. The curves of the Gaussian distribution for different values ​​of s: s₁ = 10, s₂ = 20 and s₃ = 30.

Fig. 3. shows the distribution curves corresponding to different s. This figure shows that for small s the curve is narrower, and the maximum is higher, which corresponds to more high-quality measurements.

In practice it is often necessary to determine the arithmetic mean error.
Let х₁, х₂, …, х_i, …, х_п - individual results of the measurements, each of which is characterized by the same variance. The arithmetic mean of number of measurements is defined by:

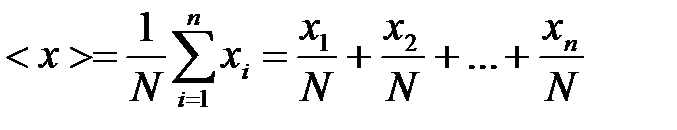. (7)

Then the dispersion of this quantity is defined as

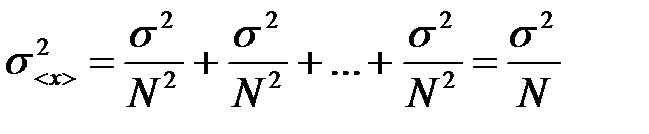, (8)

as a result,

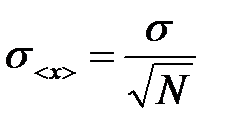. (9)

Analogically

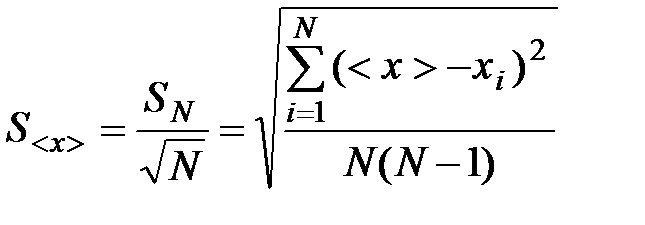. (10)

The mean square error of the arithmetic mean is the mean-square error of a separate result, divided by the square root of the number of dimensions. This is the fundamental law of increasing accuracy with increasing number of observations.

The probability that the true value lies within a certain range from <x>-Dx to <x>+Dx is called the confidence coefficient (coefficient of reliability, reliability) and the interval- a confidence interval. For sufficiently large values N confidence interval <x>±s_<х> corresponds to the a=0,68, <x>±2s_<х> corresponds to the a=0,95, <x>±3s_<х> corresponds to a=0,997.

Measure s approximation of the measured value x greatness to the true value x₀ is defined by a physical entity measured value, as well as physical and structural principles of the measurement technique, so an infinite increase in the number of measurements does not give an appreciable increase in accuracy.

Since there is no sense to strive for a very large number of measurements, then the experiment is carried out a limited number of procedures. However, for a given reliability a confidence interval, measured in fractions of s is undervalued. The question arises how the reliability depending on the number of measuring? This dependence is complex and can not be expressed in terms of elementary functions.

Multipliers determining the amount of space as a fraction of S_<х> as a function of a and N, called the coefficients of the Student, denoted by t_a,N, and exist from the tables of the Student's coefficient (Table 1).

Confidence interval D x can be calculated by the formula:

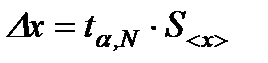. (11)
The end result, in this case, is represented as:

х = <x> ± Dx при a=К%. (12)

Obviously, when a=0,68 t_a,N>1, but when N®¥ t_a,N®1

Confidence interval of the experiment result generally corresponds to the confidence level a=0,95. If a=0,95 t_a,N>2, but with N®¥ t_a,N®2.

To assess the accuracy of the experiment one calculates the relative error of the experiment. The relative error is the error expressed in fraction of the true value of the measured values​​:

.

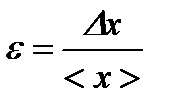It is often expressed as a percentage:

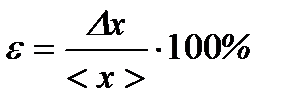. (13)

---

Дата добавления: 2015-10-26