Точечно-векторное аффинное пространство

Определение. Пусть некоторое множество 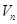состоит из элементов двух типов, которые будем называть «точками» и «векторами». Пусть при этом множество векторов образует n -мерное линейное пространство, а множество точек не пусто.

Множество 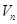называется точечно-векторным аффинным пространством, если:

1. Каждая пара точек А ₁ и A ₂, заданных в определенном порядке, определяет единственный вектор .

2. Для каждой точки А ₁, и каждого вектора 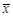существует единственная точка A ₂, такая, что .

3. Если 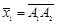и , то .

Пространство 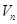называется n -мерным, если n -мерно соответствующее линейное пространство.

Пример. Данному определению удовлетворяет, очевидно, обыч­ное геометрическое пространство, в котором векторы вводятся как упорядоченные пары точек. Вторая аксиома соответствует возможности отложить любой вектор из произвольной точки, а третья аксиома со­ответствует определению сложения векторов.

4.1. Система координат в пространстве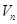

Если в пространстве V_n зафиксировать некоторую точку O, то в силу свойств 1 и 2 между всеми остальными точками и векторами устанавливается взаимно однозначное соответствие. Вектор назы­вается радиус-вектором точки А относительно точки O.

Определение. Системой координат в пространстве V_n, называется совокупность фиксированной точки O и некоторого базиса в V_n.

Координатами вектора 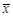в заданной сис­теме координат пространства V_n называются координаты вектора 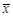относительно базиса .

Координатами точки А в данной системе ко-
ординат пространства V_n называются координаты радиус-вектора точки относительно базиса.

Всякие два базиса пространства V_n и связаны между собой формулами перехода

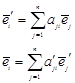
где вектор-столбцы матриц перехода 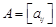и состоят из координат векторов и 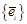соответственно в базисах и .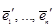

Если даны две системы координат O, и 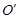, , 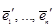то координаты любой точк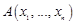и и 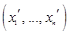относительно этих систем координат связаны соотношениями

,

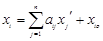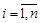
где 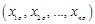– координаты точки 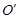в – матрица перехода.

4.2.Прямая и плоскость в V_n

Определение. Пусть в аффинном пространстве V_n заданы собственное подпространство L и фиксированный вектор 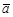.Множество

называется плоскостью в V_n. Размерностью плоскости X называется размерность соответствующего подпространства .

Одномерная плоскость пространства V_n называется прямой линией.

Плоскость размерности называется гиперплоскостью.

Две плоскости называются совпадающими, если они состоят из одних и тех же точек (векторов) пространства; в противном случае они называются несовпадающими.

Множество точек n -мерного пространства, принадлежащих как плоскости X ₁, так и плоскости X ₂, называется их пересечением, а сами плоскости X ₁ и X ₂ пересекающимися, если .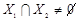

Две несовпадающие плоскост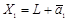и и , полученные сдвигом одного и того же подпространства L, называются параллельными.

Из определения плоскости следует, что всякая плоскость является линейным многообразием.

Всякая k -мерная плоскость может быть задана либо параметрическим уравнением

,

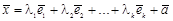где — базис в L, — произвольные числа, либо как линейное многообразие системой линейных неоднородных уравнений

ранга n - k, где 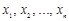— координаты вектора .

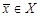В частности, всякая прямая задается либо системой линейных уравнений ранга , либо параметрическим уравнением

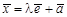
где — направляющий вектор прямой, λ — параметр. Есл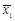и и 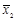— радиус-векторы двух точек прямой, то можно записать уравнение прямой, проходящей через две данные точки

,

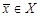
Наконец, в координатной форме можно записать каноническое уравнение прямой

,

где 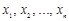— координаты точки 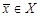, 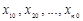— координаты некоторой фиксированной точки прямой; 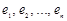-координаты направляющего вектора прямой.

Всякая гиперплоскость задается одним линейным уравнением

Примеры

1. Необходимо найти условия, необходимые и достаточные для того, чтобы две прямые и 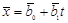пространства лежали в одной двумерной плоскости.

Предположим вначале, что две данные прямые лежат в одной плоскости с уравнением

где λ₁, λ₂ — параметры. Тогда при некоторых , , ,

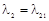а при некоторых , , .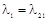

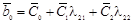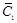Поэтому вектор принадлежит линейной оболочке векторов и 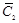. Далее для произвольной точки 1 прямой найдутся такие λ₁ и λ₂, что

Значит и . Аналогично 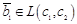. Но всякие три вектора из двумерного подпространства линейно зависимы. Следовательно, необходимым условием принадлежности прямых плоскости является линейная зависимость векторов . Обратно, пусть линейно зависимы. Тогда существуют такие λ₁ и λ₂, что . Поэтому уравнение второй прямой можно переписать в виде

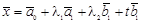
Очевидно, что теперь оба уравнения содержатся в уравнении плоскости H:

где t и τ параметры, и, следовательно, прямые принадлежат плоскости H.

2. Найти необходимые и достаточные условия для того, чтобы две прямые и проходили через одну точку, но не совпадали.

Предположим, что при некоторых значениях параметров 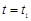для первой прямой и 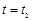для второй прямые пересекаются. Тогда

Отсюда следует, что векторы линейно зависимы. Данное соотношение далее можно при известных рассматривать как систему линейных уравнений (в координатной форме) на определение t ₁ и t ₂. Так как прямые не совпадают, то решение системы

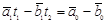(4.1)

единственно. Значит ранг матрицы системы равен 2 и векторы должны быть линейно независимы. Обратно пусть – линейно независимы, векторы – линейно зависимы. Тогда система (4.1) имеет и причем единственное решение. Следовательно, прямые пересекаются в единственной точке.

Задачи

1. Найти точку пересечения двух прямых и .

а)

, , ,

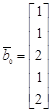б)

, , ,

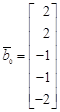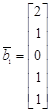
2. Найти прямую, проходящую через точку, заданную вектором и пересекающую прямые и 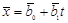, и найти точки пересечения искомой прямой с двумя данными

а) , , , ,

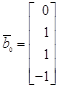б) , , , ,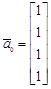

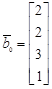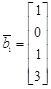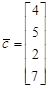
3. Описать все случаи взаимного расположения двух плоскостей

,

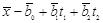
в n -мерном пространстве и указать необходимые и достаточные условия для каждого из этих случаев.

4. Доказать, что всякая система 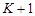точки пространства V_n определяет плоскость размерности .

5. Доказать, что линейное многообразие может быть охарактеризовано как множество векторов, содержащее вместе с любыми двумя векторам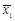и и 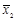их линейные комбинации 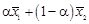при любых α.

6. Найти параметрические уравнения плоскости, заданной общими уравнениями:

7. Найти общие уравнения плоскости, заданной параметрическими уравнениями в координатной форме

Дата добавления: 2015-10-26