Волновая функция заданного уровня энергии

Решая уравнение (23) находим E – энергию одного из уровней. Затем из формул (1), (2) находим параметры

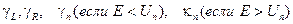
После этого приступаем к определению амплитуд волновой функции в разных областях. Существуют разные способы. Рассмотрим один из них. Положим A_L = 1, тогда остальные амплитуды найдутся из цепочки уравнений

(24)

Учитывая формулы (13) мы получаем амплитуды

Последнюю амплитуду можно найти с помощью формул (19). В результате получим

(25)

Или же B_R можно найти из системы (21). Кстати, совпадение или несовпадение результатов вычисления B_R по этим двум путям, может служить проверкой правильности вычислений.

После того, как для заданной энергии E вычислены все параметры и амплитуды, по формулам (5), (7), (8), (9) можно построить волновую функцию.

Отметим что найденная волновая функция, вообще говоря, не нормирована на единицу.

Нормирование волновой функции на единицу это отдельная задача.

1. Задание на выполнение лабораторной работы 5. Нахождение дискретных уровней энергии гетероструктуры.

Пусть гетероструктура состоит из трех ям и двух барьеров между ними как показано на рисунке 1.

Рис. 1

Параметры гетероструктур удобно задавать через списки, как показано в коде программы.

Все основные параметры гетероструктуры заносим в список Lst.

Создадим список координат внутренних областей гетероструктуры.

Удобно для наглядности создать функцию рисующую потенциальную энергию гетероструктуры.

На рисунке 1 показан результат работы программы.

Чтобы найти дискретные уровни гетероструктуры, надо создать функцию зависимости определителя (22) от энергии E.

(26)

Для вычисления определителя (22) нужно уметь вычислять матрицу M (14), и два вектора L (16) и R (18). Матрица M является произведением матриц M _n переходов между отдельными областями гетероструктуры. Поэтому нужно уметь вычислять матрицы переходов M _n (13). И, наконец, для вычисления матричных элементов и для нахождения волновых функций надо уметь вычислять базисные функции гетероструктуры (5)-(8).

Ниже приведен код для вычисления этих функций.

Используя рассмотренные формулы написать самим код функции (26).

Ниже приводится часть кода – начало и конец.

Здесь надо обратить внимание на фрагмент m=mm.m; - так с помощью оператора «точка» в пакете Mathematica выполняется умножение векторов и матриц.

Для контроля поиска дискретных уровней, и для наглядности удобно построить график функции Delta (E), чтобы увидеть, где эта функция имеет корни. Ниже приводится код построения этого графика.

Результат показан на рисунке 2.

Рис. 2

На рисунке виден корень около точки –0.2 eV. В области энергий больше нуля выбранный масштаб не позволяет рассмотреть другие корни. Поэтому выберем подходящие размеры поля вывода графика, чтобы посмотреть поведение функции Delta (E) для E > 0. Результат показан на рисунке 3.

Рис. 3

Из графиков на рисунках 2 и 3 мы видим, что гетероструктура имеет, пять дискретных уровней энергии. Один уровень меньше нуля и четыре больше нуля. Если выбирать область вывода графика вблизи нужного корня, то можно вручную найти все пять уровней энергии. Но такой способ достаточно утомителен, поэтому будем искать корни характеристического уравнения в автоматическом режиме.

Самым простым способом нахождения всех корней на заданном интервале [ x _b, x _e] является следующий способ. Двигаемся слева направо по заданному интервалу с небольшим шагом. Шаг step должен быть меньше расстояния между соседними корнями. На каждом шаге ищем корень на отрезке равном шагу. Если корня нет, то движемся дальше, если же есть, то заносим в список найденных корней. Ниже приведен фрагмент кода поиска корней.

Здесь используется библиотечная функция FindRoot. Как всякая универсальная программа она в одних случаях работает хорошо, а в других плохо. Для наших целей лучше написать свою функцию поиска корней. Самый простой и самый надежный алгоритм – это деление отрезка пополам. Ниже приводится код функции ZeroTwo, которая заменяет библиотечную функцию FindRoot.

Далее мы используем функцию ZeroTwo в функции поиска всех корней на заданном интервале следующим образом.

Далее приведен фрагмент кода для нахождения всех дискретных уровней гетероструктуры.

В результате работы программы получаем следующие пять уровней энергии.

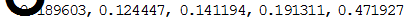
Можно сравнить полученные значения с нулями функции Delta (E) на графиках (Рис.2, Рис.3). Полученные уровни энергии обычно принято изображать на графике потенциальной энергии в виде горизонтальных линий.

Нарисуем эти линии с помощью следующего кода.

Результат показан на рисунке 4.

Рис. 4

2. Задание на выполнение лабораторной работы 5. Нахождение волновых функций дискретного спектра энергии гетероструктуры.

Для нахождения волновой функции соответствующей стационарному уровню E, необходимо вычислить амплитуды A _n, B _n волновой функции по формулам (24), (25). Чтобы воспользоваться формулами (24), (25) надо уметь вычислять матрицы переходов M _n и векторы L и R по формулам (13), (16), (18). Ниже приводится часть кода для вычисления этих матриц и векторов.

Амплитуды A _n, B _n волновой функции удобно задать одним списком, где нечетные компоненты будут соответствовать амплитудам A _n, четные амплитудам B _n. Ниже приведен код нахождения амплитуд.

Теперь по формулам (7), (8), (9) можно найти волновую функцию для данного уровня энергии. Ниже приводится соответствующий код.

Найденные волновые функции, вообще говоря, не нормированы на единицу.

Пусть интеграл от функции равен С.

Тогда легко проверить, что функция будет нормирована на единицу. Поэтому для каждой волновой функции надо найти нормировочный множитель . После этого новая волновая функция будет нормирована не единицу.

Ниже приводится код нахождения нормировочных множителей волновых функций для всех дискретных уровней гетероструктуры.

Теперь опишем алгоритм построения волновой функции, например второго уровня. Из списка уровней энергии берем второй элемент.

Для данной энергии находим все амплитуды волной функции.

Берем нужный нормировочный множитель Na[[2]], и строим график этой волновой функции.

Результат показан на рисунке 5.

Рис. 5

Следующий код позволяет построить графики всех волновых функций в цикле, вывести каждую волновую функцию по отдельности и все вместе.

Ниже показан результат работы программы.

Рис. 6 Энергия уровня

Рис. 7 Энергия уровня

Рис. 8 Энергия уровня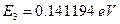

Рис. 9 Энергия уровня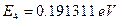

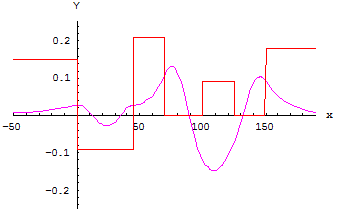
Рис. 10 Энергия уровня

Из рисунков видно, что волновые функции подчиняются правилу общему для одномерных решений уравнения Шредингера. Волновая функция основного состояния 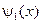не имеет узлов. Волновая функция первого возбужденного состояния имеет один узел. Следующая волновая функция имеет два узла. И, наконец, функция имеет четыре узла. Это правило удобно использовать для проверки правильности найденного решения.

На следующем рисунке приведены все волновые функции вместе.

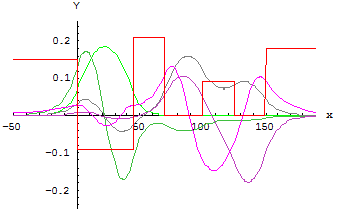
Рис. 11

3. Задание на выполнение лабораторной работы 5. Нахождение дискретного спектра и волновых функций гетероструктуры данной в варианте.

Пусть гетероструктура состоит из двух ям и барьера между ними. Параметры такой гетероструктры для каждого варианта приведены в таблице. Необходимо для своего варианта написать программу аналогичную рассмотренной выше. Найти все уровни дискретного спектра гетероструктуры и все волновые функции.

Таблица параметров гетероструктуры

Варианты	UL	U1	U2	U3	UR	d1	d2	d3
	0.5	-0.3	0.7	0.0	0.6
	0.4	-0.3	0.5	0.0	0.4
	0.5	0.0	0.5	-0.3	0.5
	0.5	0.0	0.5	0.3	0.5
	0.5	0.0	0.5	0.3	0.5
	0.5	0.0	0.5	0.0	0.5
	0.5	0.0	0.5	0.0	0.5
	0.4	0.0	0.65	0.0	0.5
	0.4	0.0	0.15	0.0	0.5
	0.4	-0.3	0.10	-0.2	0.3
	0.4	-0.3	0.6	-0.2	0.3
	0.4	-0.3	0.6	-0.2	0.3
	0.3	-0.3	0.6	-0.2	0.3
	0.6	0.0	0.45	-0.15	0.3
	0.6	0.0	0.45	-0.15	0.15
	0.2	0.0	0.45	0.0	0.2
	0.2	-0.2	0.45	0.0	0.2
	0.2	-0.2	0.45	0.1	0.2
	0.2	-0.1	0.5	-0.1	0.15
	0.3	0.0	0.8	0.0	0.3
	0.1	0.0	0.8	0.0	0.3
	0.4	0.0	0.4	-0.2	0.3
	0.3	-0.2	0.1	-0.2	0.3
	0.3	0.0	0.2	0.0	0.3
	0.15	0.0	0.2	0.0	0.3

Дата добавления: 2015-10-26