Граничные условия

Основные уравнения

Рассмотрение задачи движения электрона в системе потенциальных ям и барьеров прямоугольной формы упрощается тем, что решение уравнения Шредингера в области с постоянной потенциальной энергией U(x) = const имеет очень простой вид.

Уравнение Шредингера для стационарных состояний

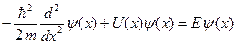(1)

в области с постоянной потенциальной энергией имеет следующие решения

Если E > U, то имеем

(2)

Если E < U, то имеем

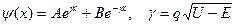(3)

где

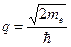
Для наших целей удобно решение уравнения Шредингера представить в следующем виде

(4)

где действительные функции f(x), g(x) определены следующим образом

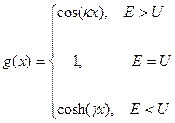(5)

Здесь d - ширина ямы или барьера, в которых ищется решение уравнения Шредингера

В дальнейшем удобно линейные размеры системы и координаты задавать в ангстремах, а энергии в электроновольтах. Тогда типичные значения расстояний d ~50 D, а энергий U, E ~ 0.5 eV. Эффективную массу электрона в гетероструктуре возьмем в 10 раз меньшую, чем для свободного электрона. В этом случае параметр q = 0.162.

При переходе через границу двух соседних областей должны выполняться граничные условия – непрерывность волной функции и ее производной. Поэтому приведем формулы для производных

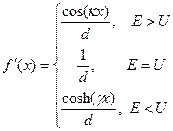
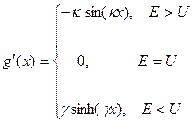(6)

Рассмотрим задачу на нахождения дискретного энергетического спектра электрона в гетероструктуре следующего вида

U

U_L U₁ U_R

U₂ U_N-1 U_N

d₁ d₂ d_N-1 d_N

E

0..... x

x₁ x₂ x₃ x_N-1 x_N x_N+1

В этой структуре имеются три характерные области. Слева в области x < x₁ энергия электрона E < U_L. Поэтому волновая функция в этой области имеет вид

(7)

Справа в области x > x_N+1 энергия электрона E < U_R. Поэтому волновая функция в этой области имеет вид

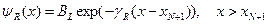(8)

Третья область состоит из N частей. В каждой из этих областей волновая функция имеет вид

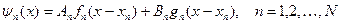(9)

где функции f_n(x), g_n(x) находятся по формулам (6)

Граничные условия

Рассмотрим граничные условия в точке x = x_n+1. Слева и справа от этой границы волновые функции имеют вид

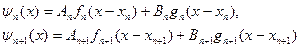(10)

В самой точке x = x_n+1 должны выполняться условия

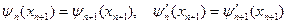(11)

После подстановки (10) в (11) получаем систему уравнений

(12)

Эту систему удобно переписать в матричном виде

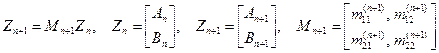(13)

где матричные элементы определяются по формулам

Нам улыбнулась удача, так как

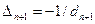
Теперь легко связать амплитуды A₁, B₁ волновой функции в области n = 1 и амплитуды A_N, B_N волновой функции в области в области n = N.

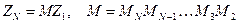(14)

Далее в точке x = x₁ сшиваем функции и производные

В результате получаем систему

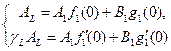(15)

которую можно записать в матричном виде

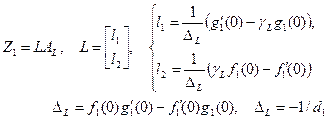(16)

Затем в точке x = x_N+1 сшиваем функции и производные

В результате получаем систему

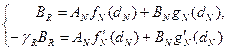(17)

которую можно записать в матричном виде

(18)

Дата добавления: 2015-10-26