Приклади розв’язання завдань контрольних робіт

Приклад 1. Знайти область визначення функції .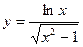

Розв’язання. Областю визначення є множина точок, для яких виконуються умови: 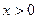, 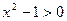. Отже, ;

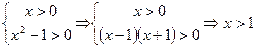Область визначення – інтервал .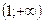

Приклад 2. Дослідити функцію на парність .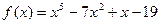

Розв’язання.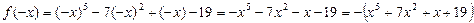

Функція ні парна, ні непарна.

Приклад 3. Побудувати графік функції .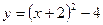

Розв’язання. Графік функції 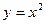відомий, це парабола.

Приклад 4. Знайти границю:

Щоб розкрити невизначеність виду 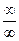задана відношенням двох многочленів, треба чисельник і знаменник розділити на найвищий степінь 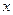у цих многочленах

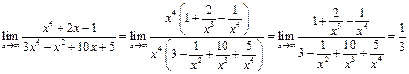
Щоб розкрити невизначеність виду 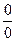задана відношенням двох многочленів, треба в чисельнику і знаменнику виділити критичний множник 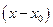і скоротити на нього

Щоб розкрити невизначеність виду 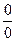задана ірраціональними виразами, необхідно позбутись від ірраціональності, помноживши на спряжений вираз

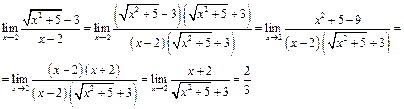
Щоб розкрити невизначеність виду 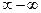задана ірраціональними виразами необхідно позбутись від ірраціональності, помноживши на спряжений вираз

Щоб розкрити невизначеність виду 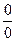задана виразами, що містять тригонометричні функції, застосовують першу важливу границю

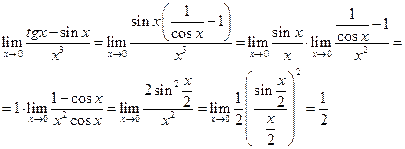
Щоб розкрити невизначеність виду застосовують другу важливу границю

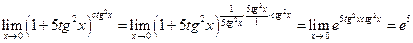
Приклад 5. Знайти похідну функції, якщо .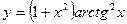

Розв’язання. За правилами та формулами диференціювання дістанемо

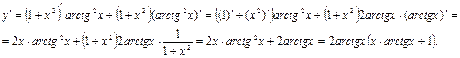
Приклад 6. Знайти похідну функції, якщо .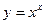

Розв’язання.

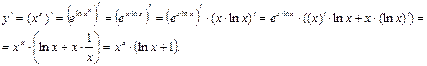
Приклад 7. Дослідити функцію 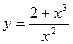і побудувати її графік.

Розв’язання.

1. Область існування функції .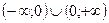

2. Графік перетинає вісь абсцис в точці .

3. Функція загального вигляду неперіодична.

4. Функція в точці 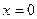має розрив другого роду і 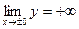, отже вісь ординат є вертикальна асимптота.

5. Похідна 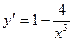дорівнює нулю при 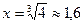і не існує при .

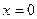Складемо таблицю і визначаємо інтервали монотонності функції.

x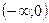
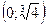
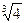
y′		не існує	-		+
y		не існує

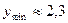
6. Друга похідна 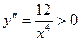всюди, крім точки 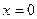, де вона не існує. Отже, крива вгнута і точок перегину немає.

7. Знаходимо похилу асимптоту.

,

.

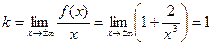Рівняння похилої асимптоти .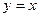

8. Будуємо графік

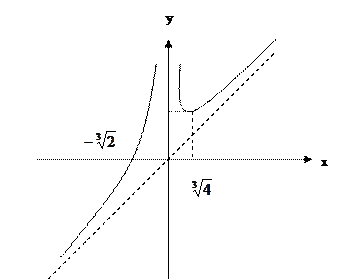
Приклад 8. Обчислити інтеграл .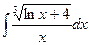

Розв’язання. При розв’язанні подібних інтегралів застосовують метод заміни змінної, а саме, введення під знак диференціала. Враховуючи, що 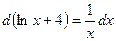, маємо

.

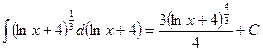Приклад 9. Обчислити інтеграл .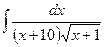

Розв’язання. При розв’язанні подібних інтегралів застосовують метод заміни змінної, а саме, підстановка.

.

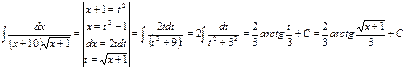Приклад 10. Обчислити інтеграл .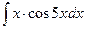

Розв’язання. При розв’язанні подібних інтегралів застосовують метод інтегрування частинами.

.

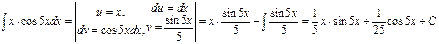Приклад 11. Обчислити інтеграл .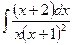

Розв’язання. Підінтегральна функція - правильний дріб, розкладемо на суму елементарних дробів

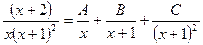, де 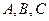- невизначені коефіцієнти. Звідси

.

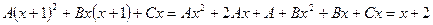
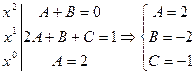Тоді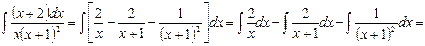

.

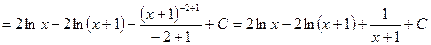Приклад 12. Обчислити інтеграл .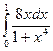

Розв’язання. Визначені інтеграли обчислюються за формулою Ньютона-Лейбніца.

.

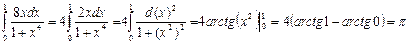Приклад 13. Обчислити визначник .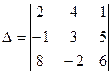

Розв’язок.

.

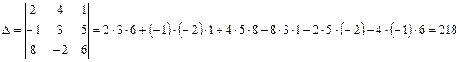Приклад 14. Знайти обернену матрицю 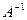до матриці 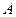. Зробити перевірку.

.

Розв’язок. 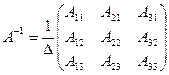, де 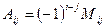- алгебраїчні доповнення елементів матриці.

.

.

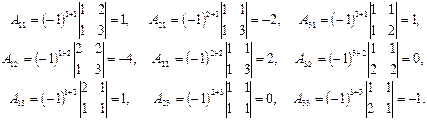
Зробимо перевірку .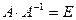

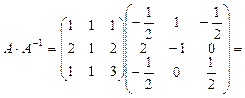
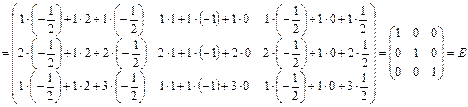
Приклад 15. Розв’язати систему лінійних рівнянь методом Крамера, методом Гауса, матричним методом.

.

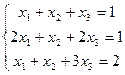Розв’язок.

1). Метод Крамера:

Знайдемо визначник системи 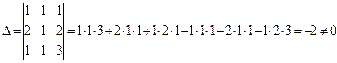, отже система має єдиний розв’язок.

; ; .

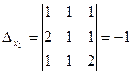За формулами Крамера ; ; .

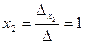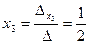2). Метод Гауса:

.

3). Матричний метод:

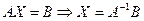
Матриц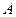і і 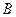нам відомі з умови, необхідно знайти матрицю 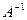(з попереднього прикладу нам відома матриця ).

, , , .

,

; ; .

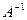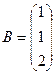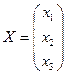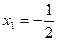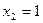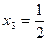Приклад 16. Дослідити систему лінійних рівнянь на сумісність і, якщо це можливо, знайти розв’язки: .

Розв’язок. система лінійних рівнянь 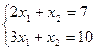– сумісна, бо має розв’язок (3, 1). З’ясуємо, скільки розв’язків має ця система; припустимо, що сукупність чисел 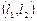є розв’язком цієї системи; тоді

або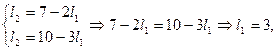

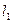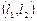підставивши у рівність замість число 3, дістанемо . Отже, розв’язок збігається з розв’язком (3, 1) і дана система має єдиний розв’язок (3, 1), тобто є визначеною системою.

Приклад 17. В трапеції 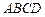відношення основи 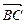до основи 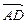дорівнює . Беручи за базис вектори 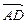і 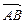, знайти координати векторів , , , , , .

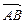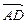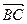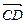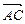Розв’язок. За умовою задачі .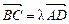

Визначаємо координати векторів:

1) ;

;

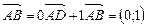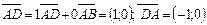
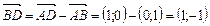4) ;

5) ;

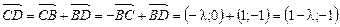6) .

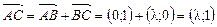Приклад 18. Скласти канонічне рівняння прямої, що проходить через дану точку М₀ паралельно вектору 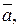якщо

.

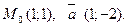
Розв’язок. Скористаємося формулою для запису канонічного рівняння прямої .

Маємо .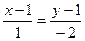

Приклад 19. Скласти канонічне рівняння еліпса, фокуси лежать на осі ОХ, причому 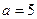і .

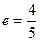Розв’язок. Оскільки 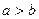, то , звідки 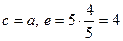. З рівності 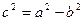визначаємо .

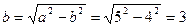Тоді шукане рівняння еліпса має вигляд .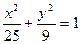

Приклад 20. Знайти рівняння параболияка має фокус і вершину в початку координат.

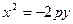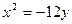Розв’язок. Оскільки фокус лежить на осі під вісю ОХ, то вісь ординат є фокальною віссю параболи, рівняння якої має вигляд . Внаслідок того, що , маємо . Тоді - шукане рівняння параболи, директрисою якої є пряма .

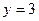Приклад 21. Знайти загальний інтеграл диференціального рівняння:

.

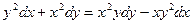Розв’язок. Перенесемо все в ліву частину і погрупуємо

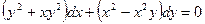
Перетворимо ліву частину рівняння

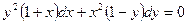
Поділивши обидві частини цього рівняння на функцію 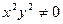, дістанемо рівняння з відокремлюванними змінними

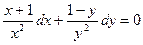, інтегруючи, яке знаходимо загальний інтеграл

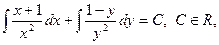або 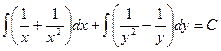, звідки

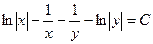, або .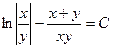

Рівняння 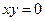має розв’язки 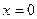і , тому прям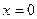і і є інтегральними кривими данного рівняння. Вони не утворюються із загального інтеграла ні при якому значенні 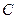. Отже, розв’язки 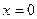і є особливими і їх слід виписувати додатково до загального інтеграла.

Приклад 22. Розв’язати рівняння: .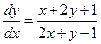

Розв’язок. Для цього рівняння 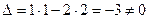, тому, поклавши 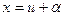, , 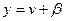дістанемо

, ; ;

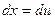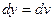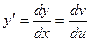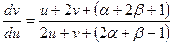, стал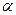і і 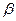доберемо так, щоб

Розв’язуючи цю систему, знайдемо , тому заміною змінної 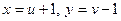задане рівняння зводиться до однорідного:

.

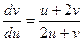За допомогою підстановки знаходимо загальний інтеграл цього рівняння:

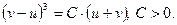
Звідси, враховуючи, що 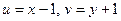, дістанемо загальний інтеграл заданого рівняння

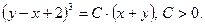
Приклад 23. Знайти розвязок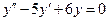

Розв’язок.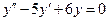

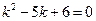
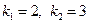
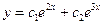
Приклад 24. Проінтегрувати рівняння в повних диференціалах: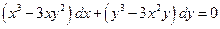

Розв’язок. Маємо .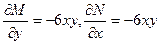

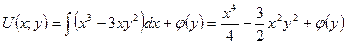, де - довільна диференційовна функція змінної 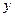. Її потрібно підібрати таким чином, щоб виконувалась рівність 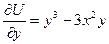. Через те, що 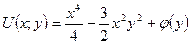, матимемо 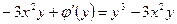. Звідси 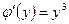, , 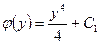отже, 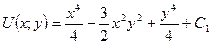. Загальний іртеграл рівняння буде .

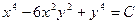Приклад 25. Дослідити ряд на збіжність:

Розв’язок. Скористаємося ознакою Д’Аламбера:

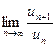, за умовою 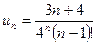, тоді .

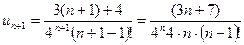Отже 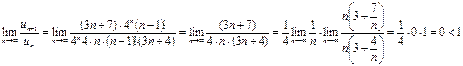заданий ряд збіжний.

Приклад 26. Дослідити ряд на збіжність: .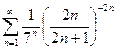

Розв’язок. Скористаємося ознакою Коші:

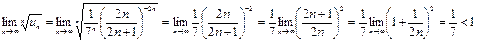заданий ряд збіжний.

Питання до заліку

Визначник другого, третього порядку. Основні властивості визначників.

Матриці. Дії над матрицями.

Обернена матриця. Ранг матриці. Елементарні перетворення матриць.

Системи лінійних рівнянь. Системи лінійних однорідних рівнянь. Теорема Кронекера-Капеллі.

Методи розв’язання систем лінійних рівнянь.

Скалярні і векторні величини. Лінійні дії з векторами.

Розклад вектора за базисом.

Системи координат.

Скалярний добуток векторів та його властивості. Векторний та мішаний добуток векторів.

Пряма на площині (різні види рівнянь прямої на площині).

Кут між двома прямими. Відстань від точки до прямої.

Площина в просторі.

Пряма лінія в просторі.

Коло. Еліпс. Гіпербола. Парабола.

Функція (поняття, способи задання, елементарні функції).

Границя функції і точці. Основні теореми про границі.

Важливі границі. Правило Лопіталя.

Методи розкриття невизначеностей і границях.

Означення похідної. Таблиця похідних.

Теореми Ферма, Ролля, Коші, Лагранжа.

Схема дослідження функції та побудова її графіка.

Невизначений інтеграл. Таблиця основних інтегралів.

Основні методи інтегрування.

Визначений інтеграл.

Обчислення площ плоских фігур (застосування визначеного інтеграла).

Питання до екзамену

Означення визначника. Основні властивості визначників.

Мінор. Алгебраїчне доповнення елемента визначника.

Визначення матриці. Різновиди матриць. Обернена матриця.

Дії над матрицями.

Базис. Ранг матриці.

Теореми про лінійно залежні і лінійно незалежні вектори.

Система лінійних рівнянь. Основні означення.

Метод Крамера розв’язання системи лінійних рівнянь. Вивести формули Крамера.

Матричний запис системи лінійних рівнянь та її розв’язок.

Розв’язування системи лінійних рівнянь методом Гауса.

Однорідна система лінійних рівнянь. Критерій сумісності системи лінійних рівнянь.

Вектори. Лінійні операції над векторами. Скалярний добуток векторів.

Векторний базис на площині і в просторі.

Лінія на площині та її рівняння. Різні види рівнянь прямої на площині.

Загальне рівняння прямої та його дослідження.

Взаємне розміщення двох прямих. Кут між двома прямими. Умови паралельності і перпендикулярності двох прямих.

Поняття лінії другого порядку. Коло. Рівняння кола.

Еліпс. Канонічне рівняння еліпса.

Гіпербола. Канонічне рівняння гіперболи.

Парабола. Канонічне рівняння параболи.

Числова послідовність. Границя послідовності.

Функція. Границя функції.

Нескінченно великі і малі функції. Основні властивості нескінченно малих величин.

Основні теореми про границі.

Неперервність функції в точці. Точки розриву.

Дії над неперервними функціями. Неперервність елементарних функцій.

Властивості функцій, неперервних на відрізку.

Задача, що приводить до поняття похідної.

Означення похідної. Механічний, фізичний та геометричний зміст похідної.

Рівняння дотичної до графіка функції в точці. Нормаль до графіка функції в точці.

Диференціювання функцій.

Теореми диференціального числення.

Монотонність функції. Найбільше і найменше значення функції.

Опуклість і вгнутість кривих. Точки перегину графіка функції.

Асимптоти кривої.

Схема дослідження функції та побудова її графіка.

Первісна. Невизначений інтеграл.

Основні властивості невизначеного інтеграла.

Методи інтегрування невизначеного інтеграла.

Інтегрування деяких ірраціональних та трансцендентних функцій.

Задача, що приводить до поняття визначеного інтеграла. Означення визначеного інтеграла.

Властивості визначеного інтеграла.

Методи обчислення визначеного інтеграла. Формула Ньютона-Лейбніца.

Застосування визначеного інтеграла.

Обчислення площ плоских фігур. Приклади.

Функція багатьох змінних: визначення, символіка.

Частинні похідні першого, другого і третього порядку функції багатьох змінних.

Диференційованість функції багатьох змінних. Повний диференціал функції багатьох змінних.

Поняття про сукупність розв’язків, загальний та частинний розв’язок диференціального рівняння. Задача Коші.

Диференціальні рівняння першого порядку з відокремлюваними змінними, алгоритм їх розв’язку.

Однорідні диференціальні рівняння першого порядку, їх розв’язок у загальному вигляді.

Лінійні диференціальні рівняння першого порядку: алгоритми їх розв’язку.

Диференціальні рівняння другого порядку. Найпростіші диференціальні рівняння другого порядку: алгоритм їх розв’язку.

Розв’язок лінійного однорідного диференціального рівняння другого порядку з постійними коефіцієнтами у випадку, якщо корені характеристичного рівняння дійсні і різні.

Розв’язок лінійного однорідного диференціального рівняння другого порядку з постійними коефіцієнтами у випадку, якщо корені характеристичного рівняння комплексні.

Означення комплексного числа. Властивості операцій над комплексними числами (доведення).

Комплексна площина. Модуль та аргумент комплексного числа.

Комплексна степінь числа е. Властивості комплексного степеня (доведення).

Алгебраїчна та тригонометрична форми запису комплексного числа. Множення та ділення комплексних чисел, записаних в тригонометричній формі (доведення).

Показникові форма запису комплексного числа. Множення та ділення комплексних чисел, записаних в показниковій формі.

СПИСОК РЕКОМЕНДОВАНОЇ ЛІТЕРАТУРИ

Гудименко Ф.С. Диференціальні рівняння. – К.: Вид-во Київ. держ. ун-ту ім. Т.Г. Шевченка, 1958. – 206 с.

Дубовик В. П., Юрик І. І. Вища математика: Навчальний посібник. – К.: Видавництво А.С.К., 2001. – С. 365-400.

Ефимов Н.В. Краткий курс аналитической геометрии. – М.: Наука, 1969. – 272 с.

Кудрявцев В. А., Демидович Б. П.. Краткий курс высшей математики: Учебное пособие. – М.: «Наука», 1978. – С. 255-278.

Курош А.Г. Курс высшей алгебры. - М.: ГИФМЛ, 1962. - 431 с.

Лейфура В. М. Та ін. Математика для студентів економічних спеціальностей вищих навчальних закладів І-ІІ рівнів акредитації. – К.: Техніка, 2003. – С. 513-537.

Матвеев Н.М. Методы интегрирования обыкновенных дифференциальных уравнений. – Минск: Высшая школа, 1974. – 768 с.

Соколенко О. І. Вища математика: Підручник. – К.: Видавничий центр „Академія”, 2002. – С. 280-304.

Филиппов А.Ф. Сборник задач по дифференциальным уравнениям. – М.: Интеграл-пресс, 1998. – 207 с.

Фаддеев Д.К., Соминский И.С. Сборник задач по высшей алгебре. – М.: Наука, 1977.–288 с.

ПРО АВТОРА

Демченко Олена Олександрівна – викладач Черкаського державного бізнес-коледжу. Закінчила математичний факультет Черкаського національного університету (2005р.).

Хотунов Владислав Ігорович – викладач Черкаського державного бізнес-коледжу. Закінчив математичний факультет Черкаського національного університету (2005р.).

Навчальне видання

ДЕМЧЕНКО Олена Олександрівна

ХОТУНОВ Владислав Ігорович

Вища математика

Методичні рекомендації

для студентів заочної форми навчання

зі спеціальності: „Обслуговування комп’ютерних та інтелектуальних систем і мереж”

Редактор Н.А. Азьмук

Коректор І.М. Прозоровська

Комп’ютерний набір О.О. Демченко

Підписано до друку 18.12.2006 р. Формат 60х80¹/₁₆

Папір офсет. Гарнітура Times New Roman. Друк офсетний.

Умов. друк. арк. 0,76. Тираж прим. Зам. № 89

Видавництво ТОВ „Інтеграл-техноімпекс”

18000, м. Черкаси, вул. Смілянська, 2

За довідками з питань реалізації

звертатись за тел. [phone]

Дата добавления: 2015-10-26