Тема 13. Числові ряди. Степеневі ряди

МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ

ЧЕРКАСЬКИЙ ДЕРЖАВНИЙ БІЗНЕС-КОЛЕДЖ

О.О. Демченко, В.І. Хотунов

ВИЩА МАТЕМАТИКА

Методичні рекомендації

Для студентів заочної форми навчання

зі спеціальності: „Обслуговування комп’ютерних та інтелектуальних систем і мереж”

Черкаси – 2006

Видання здійснено за фінансової підтримки громадської організації “Рада батьків Черкащини”

УДК 51 (076)

Рекомендовано до друку рішенням Розповсюдження та

методичної ради Черкаського тиражування

державного бізнес-коледжу без офіційного дозволу Протокол № 2 від 30 листопада 2006 р. ЧДБКзаборонено

Укладач: О.О. Демченко, В.І. Хотунов

Вища математика

Методичні рекомендації

для студентів заочної форми навчання

зі спеціальності: „Обслуговування комп’ютерних та інтелектуальних систем і мереж”

Черкаси 2006 р. – 69 с.

Методичні рекомендації містять навчальну програму з дисципліни ”Вища математика”, вимоги до виконання та оформлення контрольних робіт, варіанти контрольних робіт, приклади розв’язання типових задач та питання до іспиту.

Розраховано на студентів заочної форми навчання вищих навчальних закладів І-ІІ рівнів акредитації.

Затверджено на засіданні циклової

комісії фундаментальних дисциплін

Протокол № 4 від 01.11.06 року © О.О. Демченко, В.І. Хотунов 2006 р.

ЗМІСТ

Вступ..................................................................................................4

Тематичний план..............................................................................5

Навчальна програма......................................................................6

Вимоги до виконання та оформлення контрольних робіт.......10

Варіанти контрольних робіт.......................................................12

Приклади розв’язання завдань контрольних робіт...................47

Питання до заліку.......................................................................63

Питання до екзамену..................................................................64

Список рекомендованої літератури.............................................67

ВСТУП

Вища математика – одна з важливих математичних дисциплін, яка включає в себе елементи лінійної алгебри, аналітичної геометрії, основи математичного аналізу, які необхідні для подальшого вивчення інших предметів.

Метою курсу є формування системи теоретичних знань та практичних навичок з таких тем: елементи лінійної алгебри, аналітична геометрія, основи математичного аналізу, границі, диференціальне числення функцій однієї змінної, диференціальне числення функцій багатьох змінних, інтегральне числення функцій однієї змінної, диференціальні рівняння, ряди, комплексні числа.

Завданням курсу є оволодіння основними поняттями лінійної алгебри, аналітичної геометрії, навчитись застосовувати елементи математичного аналізу.

Предмет вищої математики – це матриці, визначники, системи лінійних рівнянь, вектори, прямі та площини, поняття та теореми математичного аналізу.

Курс передбачає аудиторні заняття та самостійну роботу студентів. Вивчення курсу завершується підсумковим екзаменом.

Методичні рекомендації з виконання контрольних робіт містять навчальний план дисципліни, порядок виконання та вимоги до оформлення контрольних робіт, перелік завдань контрольних робіт, питання до екзамену та список рекомендованої літератури.

Тематичний план

з дисципліни „вища математика”

№ з/п	Назва теми	Кількість годин
Всього	Аудиторні	Індивідуальна робота	Самостійна робота
	І семестр
1.	Визначники
2.	Матриці
3.	Системи лінійних рівнянь
4.	Вектори в лінійному просторі. Пряма на площині та в просторі
5.	Лінії другого порядку
	ІІ семестр
6.	Дійсні числа. Функція
7.	Границя функції
8.	Похідна функції. Диференціювання функцій
9.	Застосування диференціального числення для дослідження функцій
10.	Невизначений інтеграл
11.	Визначений інтеграл
	ІІІ семестр
12.	Диференціальні рівняння першого порядку
13.	Числові ряди. Степеневі ряди
Разом

Навчальна програма

з дисципліни „Вища математика”

Тема 1. Визначники

Означення визначника другого і третього порядку. Приклади обчислення визначників. Основні властивості визначників. Мінор та алгебраїчне доповнення елемента визначника.

Тема 2. Матриці

Означення матриці. Дії над матрицями. Обернена матриця. Ранг матриці. Різновиди матиць. Елементарні перетворення матриць. Зведення матриці до „ступінчастого вигляду”.

Тема 3. Системи лінійних рівнянь

Загальні відомості про системи лінійних рівнянь. Розв’язування систем лінійних рівнянь за формулами Крамера. Матричний спосіб розв’язання системи лінійних рівнянь. Розв’язання системи лінійних рівнянь методом Гауса. Однорідна система лінійних рівнянь. Критерій сумісності системи лінійних рівнянь.

Тема 4. Вектори в лінійному просторі. Пряма на площині та в просторі

Вектори. Лінійні операції над векторами. Базис. Проекція вектора на вісь. Скалярний добуток векторів. Кут між векторами. Вираження скалярного добутку через координати. Поняття про лінію на площині та її рівняння. Різні види рівнянь прямої на площині. Загальне рівняння та його дослідження. Кут між двома прямими. Умови паралельності і перпендикулярності двох прямих.

Тема 5. Лінії другого порядку

Поняття лінії другого порядку. Коло. Еліпс. Гіпербола. Парабола. Полярні рівняння кривих другого порядку. Параметричні рівняння кривих другого порядку

Тема 6. Дійсні числа. Функція

Числова послідовність. Границя послідовності. Функція. Способи задання функцій. Графіки елементарних функцій.

Тема 7. Границя функції

Границя функції. Обчислення границь функцій, границь послідовності. Дослідження функції на неперервність. Види розривів. Нескінченно великі і малі функції.

Тема 8. Похідна функції. Диференціювання функцій

Знаходження похідної функції. Рівняння дотичної, нормалі. Правила обчислення похідних. Похідна показникової, логарифмічної функції. Похідна складеної функції. Диференціал. Диференціали вищих порядків. Теореми про диференційні функції. Формула Тейлора.

Тема 9. Застосування диференціального числення для дослідження функцій

Дослідження функцій за допомогою похідних. Монотонність функції. Локальний екстремум функції. Найбільше і найменше значення функції. Опуклість і вгнутість кривих. Точки перетину. Асимптоти кривої. Схема дослідження функцій та побудова її графіка.

Тема 10. Невизначений інтеграл

Поняття первісної функції та невизначеного інтеграла. Властивості невизначеного інтеграла. Таблиця основних інтегралів. Основні методи інтегрування. Обчислення невизначеного інтеграла. Застосування основних методів інтегрування до обчислення інтегралів.

Тема 11. Визначений інтеграл

Обчислення визначеного інтеграла. Формула Ньютона-Лейбніца. Застосування основних методів до обчислення визначеного інтеграла. Невласні інтеграли першого та другого роду.

Тема 12. Диференціальні рівняння першого порядку

Диференціальних рівнянь першого порядку. Лінійні однорідні диференціальні рівняння другого порядку з постійними коефіцієнтами. Операторний метод розв’язку диференціальних рівнянь.

Тема 13. Числові ряди. Степеневі ряди

Числові ряди. Властивості числових рядів. Знакододатні ряди. Достатні умови збіжності. Знакозмінні ряди. Абсолютна і умовна збіжності. Функціональні ряди. Поняття рівномірної збіжності. Поняття степеневого ряду. Теорема Абеля. Інтервал та радіус збіжності степеневого ряду. Властивості степеневих рядів. Ряд Тейлора. Застосування ряду Тейлора до наближених обчислень. Ряди Фур’є.

Вимоги до виконання та оформлення контрольних робіт

Контрольна робота повинна бути виконана на аркушах формату А4 або в зошиті.

Титульна сторінка оформлюється наступним чином:

Умови завдань потрібно записувати повністю, без скорочень. Кожне завдання виконувати на новій сторінці. Сторінки роботи пронумерувати. Робота має містити зміст з вказівкою номерів сторінок.

Якщо в роботі є помилки або питання не розкрито, необхідно виконати вказівки викладача по доопрацюванню роботи. Робота подається за два тижні до початку сесії.

Робота, виконана не за своїм варіантом, не перевіряється і повертається студенту без оцінки. Студенти, які не одержали заліку по контрольній роботі, до екзамену не допускаються. Під час екзамену контрольна робота надається викладачу.

При вивченні курсу вищої математики студент повинен виконати три контрольні роботи, кожна з яких має 10 варіантів. Номер варіанту визначається за останньою цифрою номера залікової книжки студента.

Варіанти контрольних робіт

Контрольна робота №1

Варіант 1

Обчислити визначник .

Знайти обернену матрицю до матриці А. Зробити перевірку. .

Розв’язати систему лінійних рівнянь методом Крамера, методом Гауса, матричним методом

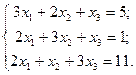
Дослідити систему рівнянь на сумісність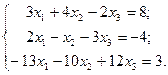

У т. О – точка перетину медіан. Довести, що .

Скласти канонічне рівняння прямої, що проходить через дану точку М₀ паралельно вектору якщо

Скласти рівняння кола, діаметром якого є відрізок прямої 4х-3у+12=0 і міститься (діаметр) між осями координат.

Скласти канонічне рівняння еліпса, який проходить через точки якщо його фокуси лежать на осі ОХ симетричного початку координат.

Варіант 2

Обчислити визначник .

Знайти обернену матрицю до матриці А. Зробити перевірку. .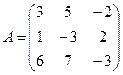

Розв’язати систему лінійних рівнянь методом Крамера, методом Гауса, матричним методом

Дослідити систему рівнянь на сумісність

Відомо, що Знайти .

Скласти канонічне рівняння прямої, що проходить через дану точку М₀ паралельно вектору якщо

Скласти рівняння кола, що дотикається до осі абсцис в точці А(2:0) і проходить через точку В(-1:3).

Скласти канонічне рівняння еліпса, фокуси якого знаходяться на осі ОХ, симетричного початку координат, якщо відстань між фокусами дорівнює 14, а ексцентриситет
дорівнює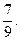

Варіант 3

Обчислити визначник .

Знайти обернену матрицю до матриці А. Зробити перевірку. .

Розв’язати систему лінійних рівнянь методом Крамера, методом Гауса, матричним методом

Дослідити систему рівнянь на сумісність

Дано: Знайти: а) б) , в) г) д)

Скласти канонічне рівняння прямої, що проходить через дану точку М₀ паралельно вектору якщо

Знайти координати центра і радіус кола

Скласти канонічне рівняння еліпса, якщо задані його вершини (0:3) і (0:-3) і відстань між фокусами дорівнює 8.

Варіант 4

Обчислити визначник .

Знайти обернену матрицю до матриці А. Зробити перевірку. .

Розв’язати систему лінійних рівнянь методом Крамера, методом Гауса, матричним методом

Дослідити систему рівнянь на сумісність

Вектори 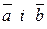утворюють кут . Відомо, що Знайти кут між векторами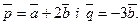

Скласти рівняння прямої, що проходить через точку (-1:3) перпендикулярно вектору

Скласти рівняння прямих, що проходить через центри кіл:

Знайти довжини осей, координат фокусів і ексцентриситет еліпса:

Варіант 5

Обчислити визначник .

Знайти обернену матрицю до матриці А. Зробити перевірку. .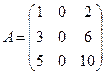

Розв’язати систему лінійних рівнянь методом Крамера, методом Гауса, матричним методом

Дослідити систему рівнянь на сумісність

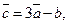Знайти модуль вектора якщо .

Серед множини прямих А(х+3)+В(у-4)=0 знайти ту, яка перпендикулярна вектору

Скласти рівняння кола, що проходить через три точки А(0:2), В(1:1), С(2:-2).

Дана гіпербола Визначити довжини осей, координати фокусів і ексцентриситет гіперболи.

Варіант 6

Обчислити визначник .

Знайти обернену матрицю до матриці А. Зробити перевірку. .

Розв’язати систему лінійних рівнянь методом Крамера, методом Гауса, матричним методом

Дослідити систему рівнянь на сумісність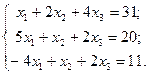

Знайти модуль якщо

Скласти рівняння прямої, що проходить через середину відрізка АВ перпендикулярно до нього, якщо А(3:-2), В(5:-4).

Скласти рівняння кола, з центром в точці (2:2) яке дотикається до прямої: 3х+у-18=0.

Скласти канонічне рівняння гіперболи, фокуси якої знаходяться на осі ОХ симетрично початку координат, якщо дійсна вісь = 6, а ексцентриситет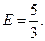

Варіант 7

Обчислити визначник .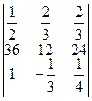

Знайти обернену матрицю до матриці А. Зробити перевірку. .

Розв’язати систему лінійних рівнянь методом Крамера, методом Гауса, матричним методом

Дослідити систему рівнянь на сумісність

В 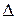АВС проведена медіана AD т. D - середина ВС. Довести, що .

Знайти кутовий коефіцієнт прямої, що проходить через точки

Скласти рівняння кола описаного навколо трикутника вершинами якого є точки А(0:1),
В(-2:0), С(0:-1).

Сума півосей гіперболи дорівнює 17, а ексцентриситет Скласти канонічне рівняння гіперболи і знайти координати її фокусів.

Варіант 8

Обчислити визначник .

Знайти обернену матрицю до матриці А. Зробити перевірку. .

Розв’язати систему лінійних рівнянь методом Крамера, методом Гауса, матричним методом

Дослідити систему рівнянь на сумісність

Вектори являються діагоналями паралелограмами ABCD. Представити вектори через .

Скласти рівняння прямої, що проходить через точку і утворює з додатнім напрямом осі ОХ кут .

Скласти рівняння кола, діаметром якого є хорда кіл: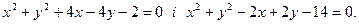

Скласти рівняння параболи з вершиною в початку координат, фокус якої знаходиться в точці перетину прямої: і віссю ординат.

Варіант 9

Обчислити визначник .

Знайти обернену матрицю до матриці А. Зробити перевірку. .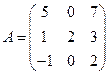

Розв’язати систему лінійних рівнянь методом Крамера, методом Гауса, матричним методом

Дослідити систему рівнянь на сумісність

ABCD-паралелограм. М і N – середини його сторін. Розкласти вектор по векторам .

Знайти кутовий коефіцієнт і початкову ординату прямої 3х+2у-6=0.

Знайти координати центра і радіус кола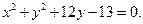

Скласти рівняння параболи з вершиною в т. і фокусом в т.

Варіант 10

Обчислити визначник .

Знайти обернену матрицю до матриці А. Зробити перевірку. .

Розв’язати систему лінійних рівнянь методом Крамера, методом Гауса, матричним методом

Дослідити систему рівнянь на сумісність

Як повинні бути розміщені вектори а і в, якщо ?

Із пучка прямих, визначених рівнянням у+2 = к (х-5) знайти ту, яка проходить через точку А (1:6).

Знайти координати центра і радіус кола

Скласти рівняння параболи, яка має фокус і проходить через початок координат, знаючи, що її віссю є вісь OY.

Контрольна робота № 2

Варіант 1

Розв’язати нерівність .

Знайти область визначення функції .

Дослідити функцію на парність .

Побудувати графік функції .

Знайти границі:

;

;

;

.

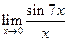Знайти похідні:

;

;

;

;

.

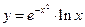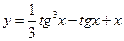Знайти інтервали монотонності функції .

Дослідити графік функції .

Обчислити інтеграли:

;

;

;

;

.

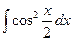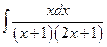Варіант 2

Розв’язати нерівність .

Знайти область визначення функції .

Дослідити функцію на парність .

Побудувати графік функції .

Знайти границі:

;

;

;

.

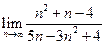Знайти похідні:

;

;

;

;

.

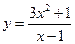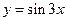Знайти інтервали монотонності функції .

Дослідити графік функції .

Обчислити інтеграли:

;

;

;

;

.

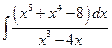Варіант 3

Розв’язати нерівність .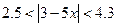

Знайти область визначення функції .

Дослідити функцію на парність .

Побудувати графік функції .

Знайти границі:

;

;

;

.

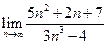Знайти похідні:

;

;

;

;

.

Знайти інтервали монотонності функції .

Дослідити графік функції .

Обчислити інтеграли:

;

;

;

;

.

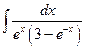Варіант 4

Розв’язати нерівність .

Знайти область визначення функції .

Дослідити функцію на парність .

Побудувати графік функції .

Знайти границі:

;

;

;

.

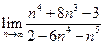Знайти похідні:

;

;

;

;

.

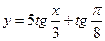Знайти інтервали монотонності функції .

Дослідити графік функції .

Обчислити інтеграли:

;

;

;

;

.

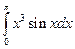Варіант 5

Розв’язати нерівність .

Знайти область визначення функції .

Дослідити функцію на парність .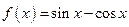

Побудувати графік функції .

Знайти границі:

;

;

;

.

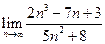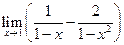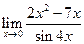Знайти похідні:

;

;

;

;

.

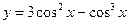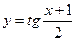Знайти інтервали монотонності функції .

Дослідити графік функції .

Обчислити інтеграли:

;

;

;

;

.

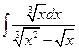Варіант 6

Розв’язати нерівність .

Знайти область визначення функції .

Дослідити функцію на парність .

Побудувати графік функції .

Знайти границі:

;

;

;

.

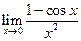Знайти похідні:

;

;

;

;

.

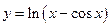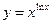Знайти інтервали монотонності функції .

Дослідити графік функції .

Обчислити інтеграли:

;

;

;

;

.

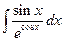Варіант 7

Розв’язати нерівність .

Знайти область визначення функції .

Дослідити функцію на парність .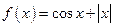

Побудувати графік функції .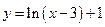

Знайти границі:

;

;

;

.

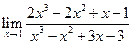Знайти похідні:

;

;

;

;

.

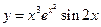Знайти інтервали монотонності функції .

Дослідити графік функції .

Обчислити інтеграли:

;

;

;

;

.

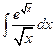Варіант 8

Розв’язати нерівність .

Знайти область визначення функції .

Дослідити функцію на парність .

Побудувати графік функції .

Знайти границі:

;

;

;

.

Знайти похідні:

;

;

;

;

.

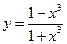Знайти інтервали монотонності функції .

Дослідити графік функції .

Обчислити інтеграли:

;

;

;

;

.

Варіант 9

Розв’язати нерівність .

Знайти область визначення функції .

Дослідити функцію на парність .

Побудувати графік функції .

Знайти границі:

;

;

;

.

Знайти похідні:

;

;

;

;

.

Знайти інтервали монотонності функції .

Дослідити графік функції .

Обчислити інтеграли:

;

;

;

;

.

Варіант 10

Розв’язати нерівність .

Знайти область визначення функції .

Дослідити функцію на парність .

Побудувати графік функції .

Знайти границі:

;

;

;

.

Знайти похідні:

;

;

;

;

.

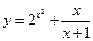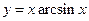Знайти інтервали монотонності функції .

Дослідити графік функції .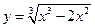

Обчислити інтеграли:

;

;

;

;

.

Контрольна робота №3

Варіант 1

Знайти загальний інтеграл диференціального рівняння: .

Знайти розв’язки рівняння: .

Проінтегрувати рівняння: .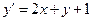

Проінтегрувати рівняння: .

Розв’язати рівняння: .

Розв’язати рівняння: .

Проінтегрувати рівняння в повних диференціалах: .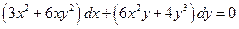

Знайти суму ряду: .

Дослідити ряд на збіжність: .

Дослідити ряд на збіжність: .

Дослідити ряд на збіжність: .

Розкласти по степенях 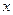функцію : .

Знайти границі за допомогою степеневих рядів: .

Варіант 2

Знайти загальний інтеграл диференціального рівняння: .

Знайти розв’язки рівняння: .

Проінтегрувати рівняння: .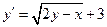

Проінтегрувати рівняння: .

Розв’язати рівняння: .

Розв’язати рівняння: .

Проінтегрувати рівняння в повних диференціалах: .

Знайти суму ряду: .

Дослідити ряд на збіжність: .

Дослідити ряд на збіжність: .

Дослідити ряд на збіжність: .

Розкласти по степенях 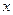функцію : .

Знайти границі за допомогою степеневих рядів: .

Варіант 3

Знайти загальний інтеграл диференціального рівняння: .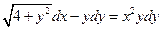

Знайти розв’язки рівняння: .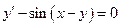

Проінтегрувати рівняння: .

Проінтегрувати рівняння: .

Розв’язати рівняння: .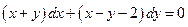

Розв’язати рівняння: .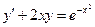

Проінтегрувати рівняння в повних диференціалах: .

Знайти суму ряду: .

Дослідити ряд на збіжність: .

Дослідити ряд на збіжність: .

Дослідити ряд на збіжність: .

Розкласти по степенях 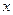функцію : .

Знайти границі за допомогою степеневих рядів: .

Варіант 4

Знайти загальний інтеграл диференціального рівняння: .

Знайти розв’язки рівняння: .

Проінтегрувати рівняння: .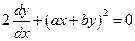

Проінтегрувати рівняння: .

Розв’язати рівняння: .

Розв’язати рівняння: .

Проінтегрувати рівняння в повних диференціалах: .

Знайти суму ряду: .

Дослідити ряд на збіжність: .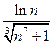

Дослідити ряд на збіжність: .

Дослідити ряд на збіжність: .

Розкласти по степенях 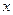функцію : .

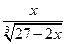Знайти границі за допомогою степеневих рядів: .

Варіант 5

Знайти загальний інтеграл диференціального рівняння: .

Знайти розв’язки рівняння: .

Проінтегрувати рівняння: .

Проінтегрувати рівняння: .

Розв’язати рівняння: .

Розв’язати рівняння: .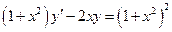

Проінтегрувати рівняння в повних диференціалах: .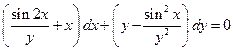

Знайти суму ряду: .

Дослідити ряд на збіжність: .

Дослідити ряд на збіжність: .

Дослідити ряд на збіжність: .

Розкласти по степенях 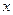функцію : .

Знайти границі за допомогою степеневих рядів: .

Варіант 6

Знайти загальний інтеграл диференціального рівняння: .

Знайти розв’язки рівняння: .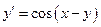

Проінтегрувати рівняння: .

Проінтегрувати рівняння: .

Розв’язати рівняння: .

Розв’язати рівняння: .

Проінтегрувати рівняння в повних диференціалах: .

Знайти суму ряду: .

Дослідити ряд на збіжність: .

Дослідити ряд на збіжність: .

Дослідити ряд на збіжність: .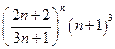

Розкласти по степенях 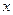функцію : .

Знайти границі за допомогою степеневих рядів: .

Варіант 7

Знайти загальний інтеграл диференціального рівняння: .

Знайти розв’язки рівняння: .

Проінтегрувати рівняння: .

Проінтегрувати рівняння: .

Розв’язати рівняння: .

Розв’язати рівняння: .

Проінтегрувати рівняння в повних диференціалах: .

Знайти суму ряду: .

Дата добавления: 2015-10-26