Упражнения и задачи. Доказать свойства эквивалентных матриц: А ~ А (рефлексивность); В ~ А Þ А ~ В

Доказать свойства эквивалентных матриц: А ~ А (рефлексивность); В ~ А Þ А ~ В (симметричность); А ~ В, В ~ С Þ А ~ С (транзитивность).

Доказать, что элементарные преобразования квадратной матрицы А равносильно умножению справа и слева на матрицы на матрицы того же порядка

, ,

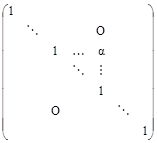
у которых на главной диагонали расположены 1 (в первой из них ещё и a), а на остальных местах во второй и третьей – нули, кроме одного элемента a.

Доказать, что при транспонировании матрицы ее ранг не меняется.

Доказать, что ранг матрицы не изменится, если к ней приписать строчку или столбец из нулей. Как изменится ранг матрицы, если к ней приписать столбец или строчку?

Найти ранг матрицы:

а) , б) , в) .

Найти ранг матрицы при различных параметрах l

а) , б) .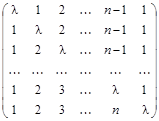

Доказать, что ранг суммы матриц не превосходит суммы рангов этих матриц.

Доказать, что ранг произведения матриц не превосходит ранга каждой из матриц – сомножителей.

Доказать, что с помощью элементарных преобразований матрицу ранга r можно привести к виду, где 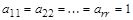, а все остальные элементы равны нулю.

Доказать, что с помощью элементарных преобразований одних строчек квадратную матрицу можно привести к “треугольному” виду, где все элементы по одну сторону от главной диагонали равны нулю.

Контрольная работа №5 по теме “Матрицы и определители”

I вариант

Входит ли в определитель соответствующего порядка произведение и, если входит, то с каким знаком: а) ; б) ?

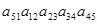Выполните умножение подстановок:

.

Вычислите определители:

а) б)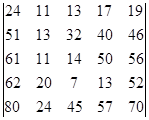

Вычислите определитель, пользуясь теоремой Лапласа:

.

Вычислите определители:

а) б) .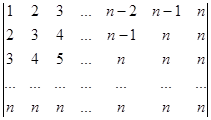

Вычислите определитель, применяя метод рекуррентных соотношений:

, (порядка 2n).

Пусть Х – матрица второго порядка. Решите уравнение: .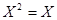

Вычислите:

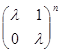а) ; б) ; в) .

Решите матричное уравнение:

.

II вариант

Входит ли в определитель соответствующего порядка произведение и, если входит, то с каким знаком: а) 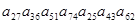; б) ?

Выполните умножение подстановок:

.

Вычислите определители:

а) 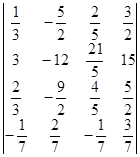б)

Вычислите определитель, пользуясь теоремой Лапласа:

.

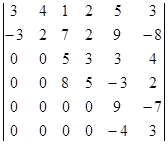Вычислите определители:

а) б) .

Вычислите определитель, применяя метод рекуррентных соотношений:

, (порядка n).

Пусть 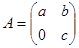, где . Найдите все такие 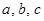, чтобы 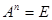при каком-нибудь натуральном n.

Вычислите:

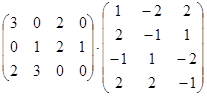а) ; б) ; в) .

Решите матричное уравнение: .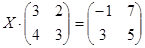

III вариант

Входит ли в определитель соответствующего порядка произведение и, если входит, то с каким знаком: а) ; б) ?

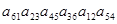Выполните умножение подстановок:

.

Вычислите определители:

а) 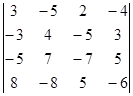б)

Вычислите определитель, пользуясь теоремой Лапласа:

.

Вычислите определители:

а) б) .

Вычислите определитель, применяя метод рекуррентных соотношений:

.

Найдите все матрицы, перестановочные с матрицей

Вычислите:

а) ; б) ; в) .

Решите матричное уравнение: .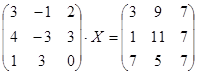

IV вариант

Входит ли в определитель соответствующего порядка произведение и, если входит, то с каким знаком: а) 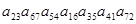; б) ?

Выполните умножение подстановок:

.

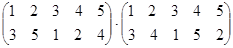Вычислите определители:

а) б)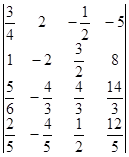

Вычислите определитель, пользуясь теоремой Лапласа:

.

Вычислите определители:

а) б) .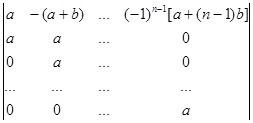

Вычислите определитель, применяя метод рекуррентных соотношений:

, (порядка n).

Пусть Х – матрица второго порядка. Решите уравнение: .

Вычислите:

а) ; б) ; в) .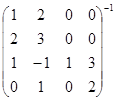

Решите матричное уравнение: .

V вариант

Входит ли в определитель соответствующего порядка произведение и, если входит, то с каким знаком: а) 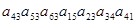; б) ?

Выполните умножение подстановок:

.

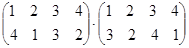Вычислите определители:

а) б)

Вычислите определитель, пользуясь теоремой Лапласа:

.

Вычислите определители:

а) 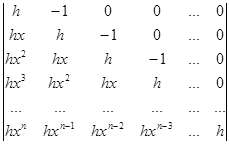б) .

Вычислите определитель, применяя метод рекуррентных соотношений:

, (порядка 2n).

Найдите все матрицы, перестановочные с матрицей .

Вычислите:

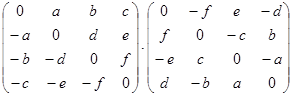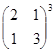а) ; б) ; в) .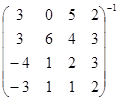

Решите матричное уравнение: .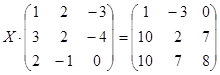

VI вариант

Подберите k и l так, чтобы перестановка (6, 3, 4, k, 7, l, 2, 1) была нечетной.

Выполните умножение подстановок:

.

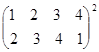Вычислите определители:

а) 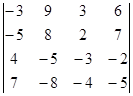б) .

Вычислите определитель, пользуясь теоремой Лапласа:

.

Вычислите определители:

а) б) .

Вычислите определитель, применяя метод рекуррентных соотношений:

.

Вычислите , если .

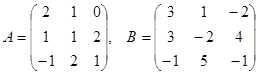Вычислите:

а) ; б) ; в) .

Решите матричное уравнение:

.

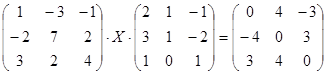VII вариант

Подберите k и l так, чтобы перестановка (4, 8, k, 2, 5, l, 1, 7) была четной.

Выполните умножение подстановок:

.

Вычислите определители:

а) 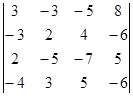б) .

Вычислите определитель, пользуясь теоремой Лапласа:

.

Вычислите определители:

а) 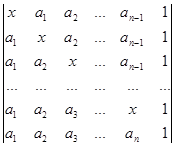б) .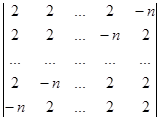

Вычислите определитель, применяя метод рекуррентных соотношений:

.

Вычислите , где ; .

Вычислите:

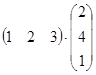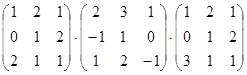а) ; б) ; в) .

Решите матричное уравнение:

.

VIII вариант

Подберите k и l так, чтобы перестановка (k, 3, 4, 7, l, 2, 6, 5) была четной

Выполните умножение подстановок:

.

Вычислите определители:

а) б)

Вычислите определитель, пользуясь теоремой Лапласа:

.

Вычислите определители:

а) 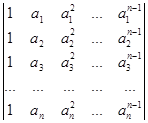б) .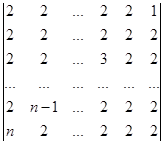

Вычислите определитель, применяя метод рекуррентных соотношений:

.

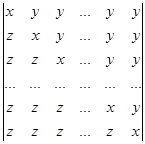Пусть Х – матрица второго порядка. Решите уравнение .

Вычислите:

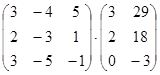а) ; б) ; в) .

Решите матричное уравнение:

.

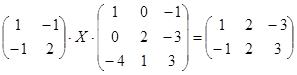IX вариант

Подберите k и l так, чтобы перестановка (7, 4, 3, k, l, 8, 5, 2) была нечетной.

Выполните умножение подстановок:

.

Вычислите определители:

а) 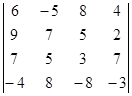б) .

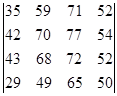Вычислите определитель, пользуясь теоремой Лапласа:

.

Вычислите определители:

а) б) .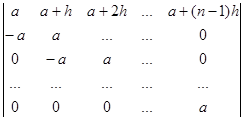

Вычислите определитель, применяя метод рекуррентных соотношений:

.

Как изменится произведение АВ матриц А и В, если переставить ‑ ый и j‑ый столбцы матрицы В.

Вычислите:

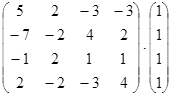а) ; б) ; в) .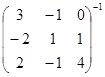

Решите матричное уравнение:

.

X вариант

Как изменится определитель порядка n, если первый столбец переставить на последнее место, а остальные столбцы передвинуть влево, сохраняя их расположение?

Выполните умножение подстановок:

.

Вычислите определители:

а) б) .

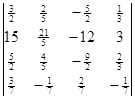Вычислите определитель, пользуясь теоремой Лапласа:

.

Вычислите определители:

а) 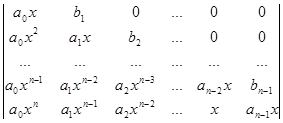б) .

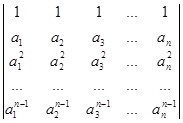Вычислите определитель, применяя метод рекуррентных соотношений:

.

Найдите матрицы, перестановочные с матрицей

Вычислите:

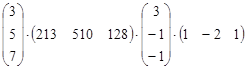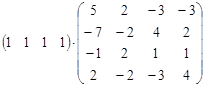а) ; б) ; в) .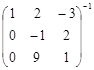

Решите матричное уравнение:

.

XI вариант

Как изменится определитель n-го порядка, если к каждой строке, начиная со второй, прибавить предыдущую, а к первой строке прибавить последнюю?

Выполните умножение подстановок:

.

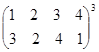Вычислите определители:

а) б)

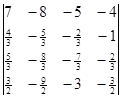
Вычислите определитель, пользуясь теоремой Лапласа:

.

Вычислите определители:

а) б) .

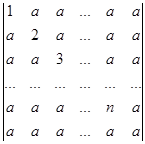Вычислите определитель, применяя метод рекуррентных соотношений:

.

Найдите 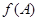, если ,

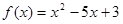Вычислите:

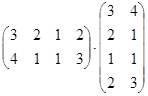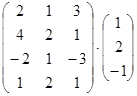а) ; б) ; в) .

Решите матричное уравнение:

.

XII вариант

Как изменится определитель n-го порядка, если к каждой строке, начиная со второй, прибавить предыдущую?

Выполните умножение подстановок:

.

Вычислите определители:

а) 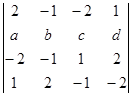б) .

Вычислите определитель, пользуясь теоремой Лапласа:

.

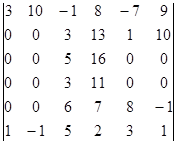Вычислите определители:

а) 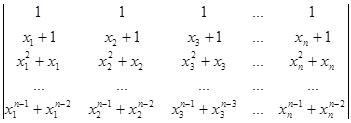б) .

Вычислите определитель, применяя метод рекуррентных соотношений:

.

Найдите все вещественные матрицы второго порядка, кубы которых равны единичной матрице.

Вычислите:

а) ; б) ;

в) .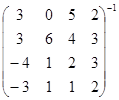

Решите матричное уравнение:

.

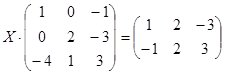XIII вариант

Как изменится определитель порядка n, если первый столбец переставить на последнее место, а остальные столбцы передвинуть влево, сохраняя их расположение?

Выполните умножение подстановок:

.

Вычислите определители:

а) б) .

Вычислите определитель, пользуясь теоремой Лапласа:

.

Вычислите определители:

а) 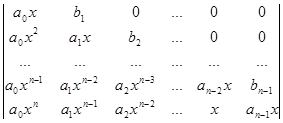б) .

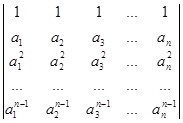Вычислите определитель, применяя метод рекуррентных соотношений:

.

Найдите матрицы, перестановочные с матрицей

Вычислите:

а) ; б) ;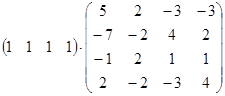

в) .

Решите матричное уравнение:

.

XIV вариант

Выберите значения i и k так, чтобы произведение 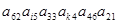входило в определитель 6-го порядка со знаком «минус».

Выполните умножение подстановок:

.

Вычислите определители:

а) 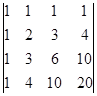б)

Вычислите определитель, пользуясь теоремой Лапласа:

.

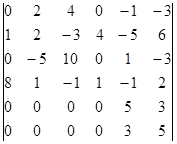Вычислите определители:

а) 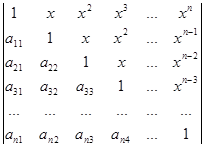б) .

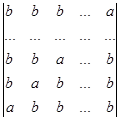Вычислите определитель, применяя метод рекуррентных соотношений:

.

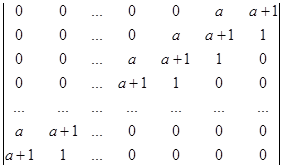Найдите 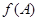, если ,

Вычислите:

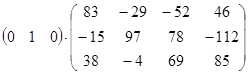а) ; б) ; в) .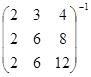

Решите матричное уравнение:

.

XV вариант

Как изменится определитель n-го порядка, если его строки записать в обратном порядке?

Выполните умножение подстановок:

.

Вычислите определители:

а) б) .

Вычислите определитель, пользуясь теоремой Лапласа:

.

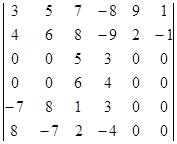Вычислите определители:

а) б) .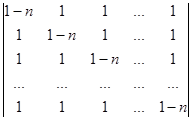

Вычислите определитель, применяя метод рекуррентных соотношений:

.

Докажите. Что каждая матрица А второго порядка 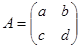удовлетворяет уравнению: .

Вычислите:

а) ; б) ; в) .

Решите матричное уравнение: .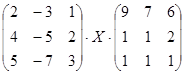

XVI вариант

Как изменится определитель n-го порядка, если i- ую строку переставить на последнее место, а (i +1)-ю и все последующие строки передвинуть вверх, сохраняя их расположение?

Выполните умножение подстановок:

.

Вычислите определители:

а) б) .

Вычислите определитель, пользуясь теоремой Лапласа:

.

Вычислите определители:

а) б) .

Вычислите определитель, применяя метод рекуррентных соотношений:

.

Найдите все матрицы второго порядка, кубы которых равны нулевой матрице.

Вычислите:

а) ; б) ; в) .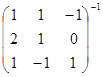

Решите матричное уравнение:

.

XVII вариант

Как изменится определитель n-го порядка, если каждый его элемент заменить сопряженным числом?

Выполните умножение подстановок:

.

Вычислите определители:

а) б)

Вычислите определитель, пользуясь теоремой Лапласа:

.

Вычислите определители:

а) б) .

Вычислите определитель, применяя метод рекуррентных соотношений:

.

Найдите все матрицы, перестановочные с матрицей

Вычислите:

а) ; б) ; в) .

Решите матричное уравнение:

.

XVIII вариант

Как изменится определитель n-го порядка, если каждый его элемент умножить на -1?

Выполните умножение подстановок:

.

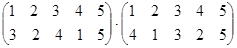Вычислите определители:

а) б) .

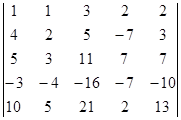Вычислите определитель, пользуясь теоремой Лапласа:

.

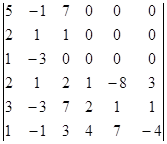Вычислите определители:

а) б) .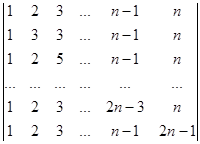

Вычислите определитель, применяя метод рекуррентных соотношений:

.

Докажите, что равенство АВ-ВА=Е не выполняется ни для каких матриц А и В.

Вычислите:

а) ; б) ; в) .

Решите матричное уравнение:

.

XIX вариант

С каким знаком входит в определитель n-го порядка а) произведение элементов главной диагонали; б) побочной диагонали?

Выполните умножение подстановок:

.

Вычислите определители:

а) б) .

Вычислите определитель, пользуясь теоремой Лапласа:

.

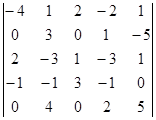Вычислите определители:

а) б) .

Вычислите определитель, применяя метод рекуррентных соотношений:

.

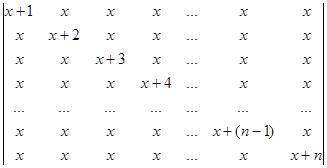Как изменится произведение АВ матриц А и В, если переставить i –ую и j –ую строки матрицы А?

Вычислите:

а) 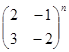; б) ; в) .

Решите матричное уравнение:

.

XX вариант

Подберите k и l так, чтобы в определителе 6-го порядка входило произведение 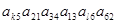со знаком плюс.

Выполните умножение подстановок:

.

Вычислите определители:

а) б) .

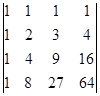Вычислите определитель, пользуясь теоремой Лапласа:

.

Вычислите определители:

а) 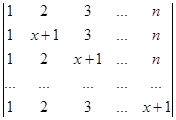б) .

Вычислите определитель, применяя метод рекуррентных соотношений:

.

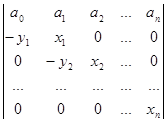Найдите 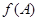, если ; .

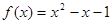Вычислите:

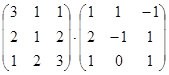а) ; б) ; в) .

Решите матричное уравнение:

.

XXI вариант

Подберите k и l так, чтобы в определителе 6-го порядка входило произведение 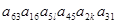со знаком плюс.

Выполните умножение подстановок:

.

Вычислите определители:

а) 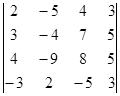б) .

Вычислите определитель, пользуясь теоремой Лапласа:

.

Вычислите определители:

а) б) .

Вычислите определитель, применяя метод рекуррентных соотношений:

.

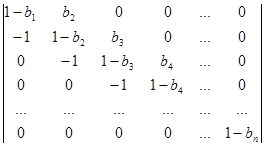Докажите, что равенство АВ-ВА, если

Вычислите:

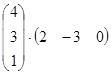а) ; б) ; в) .

Решите матричное уравнение:

.

XXII вариант

Подберите k и l так, чтобы в определителе 6-го порядка входило произведение со знаком минус.

Выполните умножение подстановок:

.

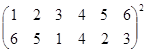Вычислите определители:

а) 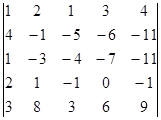б) .

Вычислите определитель, пользуясь теоремой Лапласа:

.

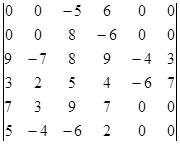Вычислите определители:

а) б) .

Вычислите определитель, применяя метод рекуррентных соотношений:

.

Найдите 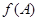, если ;

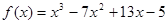Вычислите:

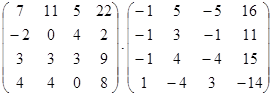а) ; б) ; в) .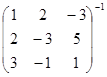

Решите матричное уравнение:

.

XXIII вариант

Подберите k и l так, чтобы в определителе 6-го порядка входило произведение со знаком минус.

Выполните умножение подстановок:

.

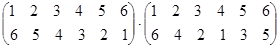Вычислите определители:

а) б)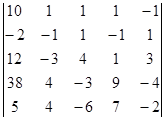

Вычислите определитель, пользуясь теоремой Лапласа:

.

Вычислите определители:

а) б) .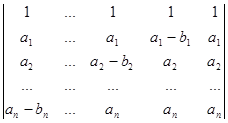

Вычислите определитель, применяя метод рекуррентных соотношений:

.

Найдите все матрицы, перстановочные с матрицей .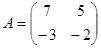

Вычислите:

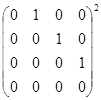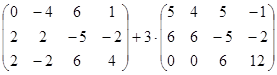а) б) ; в) .

Решите матричное уравнение:

.

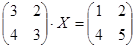XXIV вариант

Как изменится определитель, если все столбцы его написать в обратном порядке?

Выполните умножение подстановок:

.

Вычислите определители:

а) 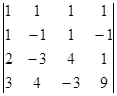б) .

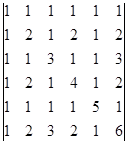Вычислите определитель, пользуясь теоремой Лапласа:

.

Вычислите определители:

а) б) .

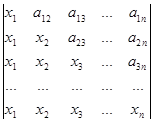Вычислите определитель, применяя метод рекуррентных соотношений:

.

Найдите все матрицы, перестановочные с матрицей

.

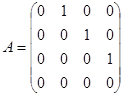Вычислите:

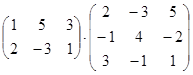а) ; б) ; в) .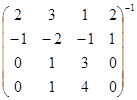

Решите матричное уравнение:

.

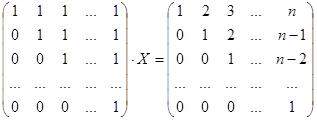XXV вариант

Подберите k и l так, чтобы в определителе 5-го порядка входило произведение со знаком плюс.

Выполните умножение подстановок:

.

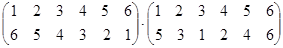Вычислите определители:

а) 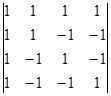б) .

Вычислите определитель, пользуясь теоремой Лапласа:

.

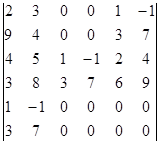Вычислите определители:

а) 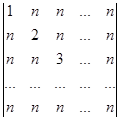б) .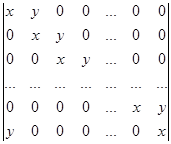

Вычислите определитель, применяя метод рекуррентных соотношений:

.

Найдите все матрицы, перестановочные с матрицей:

.

Вычислите:

а) ; б) ; в) .

Решите матричное уравнение:

.

XXVI вариант

Входит ли в определитель 5-го порядка произведение: а) ; б) ?

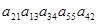Выполните умножение подстановок:

.

Вычислите определители:

а) б) .

Вычислите определитель, пользуясь теоремой Лапласа:

.

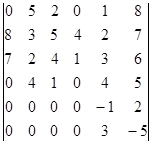Вычислите определители:

а) 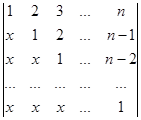б) .

Вычислите определитель, применяя метод рекуррентных соотношений:

.

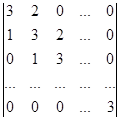Найдите определитель произведения матрицы на транспонированную матрицу.

Вычислите:

а) 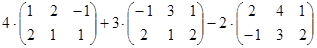б) ; в) .

Решите матричное уравнение:

.

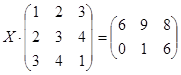XXVII вариант

С каким знаком в определитель 6-го порядка входит произведение: ?

Выполните умножение подстановок:

.

Вычислите определители:

а) 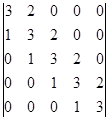б) .

Вычислите определитель, пользуясь теоремой Лапласа:

.

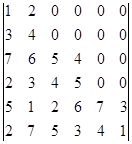Вычислите определители:

а) 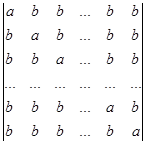б) .

Вычислите определитель, применяя метод рекуррентных соотношений:

.

Найдите все матрицы, перестановочные с матрицей:

.

Вычислите:

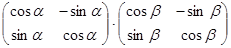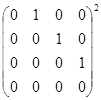а) ; б) ; в) .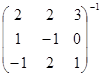

Решите матричное уравнение:

.

XXVIII вариант

С каким знаком в определитель 6-го порядка входил произведение ?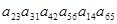

Выполните умножение подстановок:

.

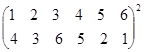Вычислите определители:

а) 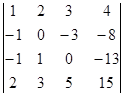б) .

Вычислите определитель, пользуясь теоремой Лапласа:

.

Вычислите определители:

а) б) .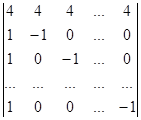

Вычислите определитель, применяя метод рекуррентных соотношений:

.

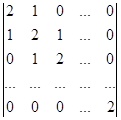Вычислите АВ-ВА, если

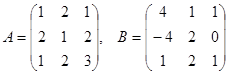
Вычислите:

а) 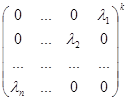; б) ; в) .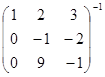

Решите матричное уравнение:

.

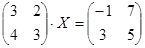XXIX вариант

Подберите k и l так, чтобы перестановка (1, k, 2, 5, l, 4, 8, 9, 7) была нечетной.

Выполните умножение подстановок:

.

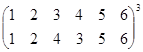Вычислите определители:

а) 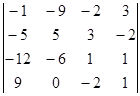б) .

Вычислите определитель, пользуясь теоремой Лапласа:

.

Вычислите определители:

а) б) .

Вычислите определитель, применяя метод рекуррентных соотношений:

.

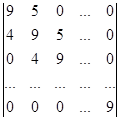Найдите все вещественные матрицы второго порядка, четвертые степени которых равны единичной матрице.

Вычислите:

а) ; б) ; в) .

Решите матричное уравнение:

.

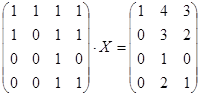XXX вариант

Подберите k и l так, чтобы перестановка (1, 2, 7, 4, k, 5, 6, l, 9) была четной.

Выполните умножение подстановок:

.

Вычислите определители:

а) 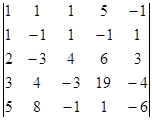б) .

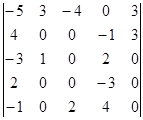Вычислите определитель, пользуясь теоремой Лапласа:

.

Вычислите определители:

а) б) .

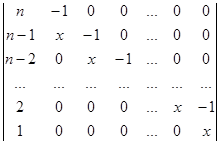Вычислите определитель, применяя метод рекуррентных соотношений:

.

Найдите все матрицы, перестановочные с матрицей:

.

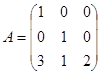Вычислите:

а) 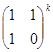; б) ; в) .

Решите матричное уравнение:

.

Дата добавления: 2015-10-23