Протокол № 5 від 26.05.2010 р.

Кафедра автоматики та електропривода

МЕТОДИЧНІ ВКАЗІВКИ ДО ВИКОНАННЯ КУРСОВОЇ

ТА КОНТРОЛЬНОЇ РОБОТИ

(для студентів денної та заочної форми навчання)

з дисципліни «Теорія автоматичного керування»

Полтава 2010

Методичні вказівки до виконання курсової та контрольної роботи з дисципліни «Теорія автоматичного керування». Полтава: ПолтНТУ 2010. – 37 с.

Укладач: В.М. Галай.

Рецензент: О.В. Шульга, кандидат тех. наук, доцент.

Відповідальний за випуск: А.М. Сільвестров, доктор тех. наук, професор.

Затверджено науково-методичною

Радою університету

Протокол № 5 від 26.05.2010 р.

Коректор Зайчук Є.В.

Комп’ютерна верстка Колеснік Є.А.

Мета курсової (контрольної) роботи з теорії автоматичного керування (ТАК) - навчитися застосовувати одержані теоретичні знання при технічних розрахунках, самостійно розв'язувати задачі аналізу автоматичних систем керування (АСК), синтезу корегувальних пристроїв (КП), що забезпечують задані показники якості.

1. Зміст пояснювальної записки

Основна частина пояснювальної записки повинна містити в собі наступний матеріал:

1. Завдання на курсову роботу;

2. Коротку характеристику автоматичної системи керування (АСК);

3. Вибір виконавчого двигуна (в окремих завданнях генератора);

4. Складання диференціальних рівнянь окремих елементів АСК і визначення їх передавальних функцій;

5. Складання структурної (алгоритмічної) схеми АСК;

6. Розрахунок коефіцієнтів передачі і сталих часу електродвигуна;

7. Визначення передавальних функцій АСК без корегувальної частини;

8. Визначення усталених помилок АСК без корегувального пристрою;

9. Дослідження АСК без корегувального пристрою на стійкість;

10.Вибір корегувального пристрою із умов заданих показників якості АСК;

11. Перевірка показників якості перехідного процесу скорегованого АСК.

2. Методичні вказівки з виконання окремих розділів курсової роботи

Завдання на курсову роботу

Для електромеханічної слідкуючої системи з потенціометричним вимірювальним пристроєм, функціональна схема якої показана на рисунку 1, потрібно:

1. Описати принцип дії системи.

2. За диференціальними рівняннями окремих елементів скласти диференційне рівняння розімкненої, замкненої системи та похибки.

3. За отриманими диф. рівняннями визначити передавальні функції окремих елементів, розімкненої системи, замкненої системи та похибки.

4. Нарисувати структурну (алгоритмічну) схему системи.

5. Визначити граничний коефіцієнт підсилення системи.

6. Вибрати коефіцієнт підсилення електронного підсилювача таким, щоб запас стійкості системи за підсиленням знаходився в діапазоні 2-3.

7. Визначити і побувати:

а) перехідну функцію замкненої системи h(t);

б) амплітудно-фазову характеристику замкненої системи АФЧ;

в) логарифмічні частотні характеристики розімкненої системи ЛЧХ,

8. Виконати корегування слідкуючої системи за допомогою пасивної диференціальної ланки (Рис.2).

9. Визначити передавальну функцію розімкненої і замкненої корегувальної системи та похибки.

10. Побудувати логарифмічну амплітудно-частотну і фазочастотну характеристики розімкненої корегованої системи і вибрати потрібний коефіцієнт підсилення електронного підсилювача так, щоб запас стійкості за амплітудою складав 2-3.

11. Визначити та побудувати перехідну функцію замкненої корегованої системи і за нею визначити показники якості перехідного процесу корегованої системи.

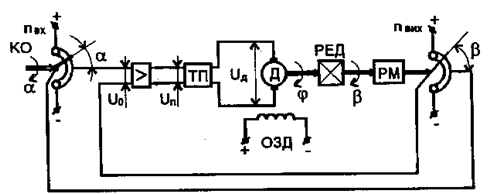
Рис.1. Функціональна схема електромеханічної слідкуючої системи з потенціометричним вимірювальним пристроєм

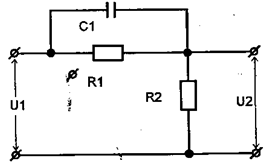
Рис.2. Електрична схема пасивної диференціальної ланки

2.1. Оформлення завдання до курсової роботи

Завдання наведено в методичних вказівках, які знаходяться на кафедрі і видаються викладачем індивідуально.

В завданні вказують:

• тему курсової роботи;

• вихідну принципову схему замкненої АСК;

• вихідні дані для розрахунку;

• вимоги, до якісних показників заданої АСК: допустимі помилки в встановле­ному режимі – статичну e_ст, і швидкісну e_шв; допустиме перерегулювання s_мах, максимальний час перехідного процесу t_р.мах.

• окремі зауваження, зв'язані з конкретною специфікою схемних розрахую.

Усі схеми АСК, наведені в завданні, повинні корегуватися в процесі розрахунку. Вихідні дані для розрахунку: орієнтовна потужність, напруга живлення електродвигуна або генератора в залежності від схеми завдання, число обертів електродвигуна, момент інерції навантажувального пристрою, для слідкуючих систем максимальна частота обертання керованого об'єкту, числові значення параметрів (сталі часу і коефіцієнти підсилення магнітних напівпровідникових підсилювачів, тиристорних перетворювачів, коефіцієнти передачі потенціометрів, генераторів, сельсинів, криві намагнічування обмоток збудження електричних машин, передавальні числа редукторів).

У завданні вказано умови визначення показників якості при прийомі навантаження або при стрибкоподібній зміні вхідної величини.

У цьому розділі пояснювальної записки повинна бути накреслена вихідна схема АСК, наведені вихідні дані до розрахунку, сформульовані завдання, які потрібно розв'язати при виконанні курсової роботи. Завдання визначені змістом роботи.

Таблиця 1. Вихідні дані для розрахунку

2.2. Коротка характеристика АСК

Виконання курсової роботи з ТАК потрібно починати з вивчення принципу роботи АСК, заданої у вигляді початкової схеми.

Даючи коротку характеристику АСК, у пояснювальній записці необхідно сформулювати мету керування (алгоритм функціонування), принцип керування, вказати функціональне призначення кожного елементу схеми (керованого об'єкту КО, автоматичного керуючого пристрою АКП, що складається з вимірювального елементу ВЕ, елементу порівняння ЕП, перетворювача П, підсилювача У), визначити, яка величина в системі являється вихідною, які величини виконують роль зовнішніх впливів, дослідити шляхи і напрямки проходження задавального і збурюючого сигналів через АСК.

У завданні приведено системи, побудовані за принципом відхилення, мета керування яких або підтримувати постійну величину, рівну заданому значенню (АСК стабілізації), або змінювати вихідну величину за невідомим раніше закону (слідкуючі АСК).

Потрібно пам'ятати, що у системах, побудованих за принципом відхилення, обов'язково повинен бути головний від'ємний зворотній зв'язок ГЗЗ, призначення якого подати вихідний сигнал на вхід системи (на елемент порівняння). Різниця між задавальною дією і сигналом зворотного зв'язку є сигналом помилки.

Потрібно мати на увазі, що елемент порівняння часто не має власного конструктивного виконання. Один елемент в системі може виконувати дві функції. Наприклад, магнітний підсилювач може бути одночасно підсилюючим елементом і елементом порівняння; сельсини що працюють в трансформаторному режимі, у слідкуючій системі одночасно виконують функції ІЕ, ЕС, П.

Даючи характеристику АСК, потрібно коротко зупинитися на принципові дії, характерних особливостях окремих елементів схеми, таких, як магнітний підсилювач, тиристорний перетворювач та ін.

2.3. Вибір виконавчою електродвигуна і генератора

У завданні приводиться орієнтовна потужність, оберти і напруга. За вказаними даними необхідно обрати двигун або генератор. Вибір двигуна закінчується випискою із каталогу або іншої довідкової літератури усіх даних із вказівкою джерела.

Якщо виконавчий двигун живиться від генератора, то потрібно вибрати і генератор, при цьому потрібно врахувати, що при різного роду втратах (електричних, теплових, механічних) потужність генератора повинна компенсувати втрати потужності при передачі енергії до наступного елементу або до двигуна. Вибір генератора закінчується випискою його повних каталогових даних.

2.4. Складання диференціальних рівнянь окремих елементів АСК і визначення їх передавальних функцій

Для складання диференціальних рівнянь окремих елементів АСК необхідно передусім систему розчленувати на окремі елементи, далі скласти структурну (функціональну) схему. При цьому усі елементи на функціональній схемі представляються з точки зору їх функціонального призначення і розподіляються в тій послідовності, в якій вони працюють в схемі. Кожний елемент на функціональній схемі зображується прямокутником, а зв'язок між окремими елементами прямими лініями з стрілками, що вказують напрямок дії даного елементу на подальші з вказівками фізичної величини, що характеризує вплив.

Потрібно розрізняти два типи зовнішніх впливів на систему автоматичного керування:

а) задавальний (керуючий) вплив x₀(t), який повинен, можливо більш точно, відтворюватися системою;

б) збурюючий вплив f(t), дія якого в системі автоматичного керування (САК) повинна, можливо більш повно, пригнічуватись.

Як приклад на Рис. 1 та Рис. 2 показано принципову і структурну (функціональну) схеми системи стабілізації напруги генератора.

Студент повинен чітко уявити принцип дії кожного елемента схеми. Далі для кожного елемента відповідно до структурної (функціональної) схемою системи потрібно записати диференціальне рівняння. Слід відмітити, що елемент у функціональному відношенні за перетворенням вхідного сигналу може являтися кількома диференціальними рівняннями.

Диференціальне рівняння елемента складається на основі відповідних фізичних законів, що визначають зв'язок між його вхідними і вихідними змінними. При цьому повинні враховуватись тільки основні процеси, що відбуваються в даному елементі, а другорядними процесами нехтують. Слід нехтувати нелінійностями статичних характеристик елементів. Враховуючи вище сказане студент в пояснюючій записці повинен вказати усі припущення, які ним були прийняті при складанні диференціальних рівнянь кожного елементу структурної (функціональної) схеми АСК.

При вказаних допущеннях диференціальне рівняння кожного елемента має відносно невисокий порядок, не вище другого, і повинно бути лінійним.

При запису диференціального рівняння вихідна величина у(t) та її похідні повинні стояти в лівій частині, причому на першому місці потрібно поставити похідну вищого порядку; вихідна величина повинна входити в рівняння з коефіцієнтом, рівним одиниці; вхідні величини х(t), f(t), а у більш загальному випадку їх похідні та інші члени розташовуються у правій частині рівняння.

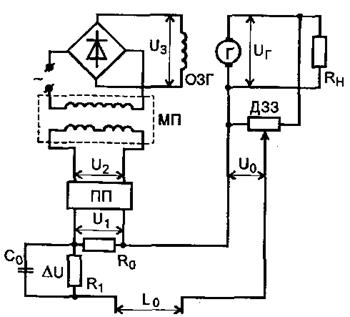
Рис.1. Принципова схема стабілізації напруги генератора

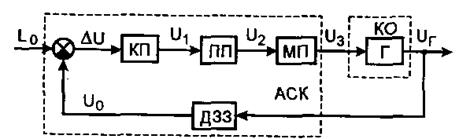
Рис. 2. Структурна (функціональна) схема стабілізації напруги генератора.

Рівняння можуть бути записані у диференційній та операторній (символічній) формі. Так, наприклад, рівняння аперіодичної ланки у диференціальній формі має вигляд:

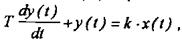(1)

або в операторній формі:

(2)

Операторна форма більш компактна форма запису ніж звичайна.

Слід пам'ятати що у ТАК використовується інша, зовні схожа, та принципово відмінна від звичайної операторної форми запису, так звана операційна форма запису.

Якщо з змінною х(t) провести перетворення Лапласа, то отримаємо зображення функції:

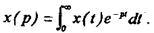
При нульових початкових умовах перша похідна від х(t) буде мати вигляд р·х(р), друга – р²·х(р) і т. д. Інтеграл від х(t) буде мати вигляд х(р)/р. Наприклад, рівняння аперіодичної ланки, записане в операційній формі, має вигляд:

(Тр + 1)·у(р)=k·х(р). (3)

Потрібно чітко уявити, що рівняння одного і того ж елемента записані в операційній формі при нульових початкових умовах і в операторній (символічній) зовсім однакові. Але вони принципово відрізняються одне від іншого.

Рівняння (2), записане в операторній формі, є диференціальним, у ньому літера р означає оператор диференціювання (d/dt, а змінні х(t), у(t) є реальними функціями часу. Рівняння (3) алгебраїчне, у ньому р є незалежною комплексною змінною, а величини х(р), та у(р) є відображеннями за Лапласом фізичних величин х(t) та у(t).

Потрібно пам'ятати, що від операторної до операційної форми формально можна перейти шляхом заміни позначень змінних як функцій часу t позначеннями цих змінних як функцій комплексної змінної р, але це можна робити тільки в тому випадку, коли початкові умови для диф. рівняння нульові. У іншому випадку у операційному алгебраїчному рівнянні з'являться додаткові члени, що враховують початкові умови.

Операційна форма запису рівнянь елементів проста і зручна так як перетворювати і розв'язувати алгебраїчне рівняння значно простіше, ніж диференційне, якраз це і забезпечує її широке використання в ТАК.

Для отримання передавальної функції елемента, як відомо, потрібно диф. рівняння записати в операційній формі для нульових початкових умов і взяти відношення зображень за Лапласом вихідної у(р) та вхідної х(р) величин, передавальна функція аперіодичної ланки відповідно з виразом (3):

(4)

Для полегшення складання математичних моделей елементів АСК, що є у завданні, нижче наведені приклади складання диф. рівнянь цих елементів.

2.4.1. Диференційне рівняння і передавальна функція двигуна постійного струму з незалежним збудженням при постійному потоці збудження і непостійних напрузі на якорі і моменті статичних опорів на валу двигуна

Диф. рівняння двигуна складено при наступних допусках;

1) система абсолютно жорстка, тобто двигун має одну степінь свободи;

2) маса частин, що обертаються постійна;

3) статичний момент, приведений до валу двигуна, сталий;

4) реакція якоря скомпенсована;

5) залежність кутової швидкості обертання вала двигуна від напруги якоря U_я лінійна;

6) потік двигуна незмінний, тобто Ф = const,

7) температура обмоток не змінюється.

При складанні рівняння двигуна використовують другий закон Ньютона і другий закон Кірхгофа, тобто закони електричної і механічної рівноваги.

Припускаючи, що обертовий момент двигуна М використовується на подолання динамічного моменту, обумовленого моментом інерції І статичного моменту навантаження М_с, отримуємо рівняння моментів:

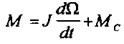(5)

де 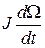- динамічний момент у кгм².

Рухаючий момент електричного двигуна у Нм:

М = кІ_яФ (6)

де 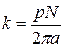- стала машини, визначається за каталоговим даним; (7)

р - число пар полюсів;

М - число активних стержнів;

а - число паралельних гілок;

І_я - струм якоря, А;

Ф - потік двигуна, Вб.

Тоді вираз (5) із урахуванням (6) можна записати:

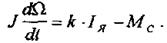(8)

У рівняння (8) входять дві незалежні змінні W, І_я. Через це необхідно знати додаткову залежність, що зв’язує ці величини між собою. Такою залежністю є рівняння електричної рівноваги ланцюга якоря. При прийнятих раніше допущеннях 4) та 7) воно має вигляд

(9)

де L_я - індуктивність ланцюга якоря:

R_я - опір якоря;

kФW - ЕРС обертання;

U_я - напруга ланцюга якоря.

Підставивши І_я із (9) у (8), після перетворень одержимо:

– передавальний коефіцієнт двигуна за напругою якоря;   – передавальний коефіцієнт двигуна за статичним моментом (за збурюючим впливом).

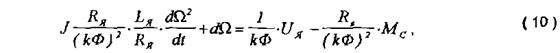
Прийняті позначення (11), (12), (13), (14), підставивши у (10), ц кінці отримаємо диф. рівняння двигуна, записане відносно регульованої величини W, при вхідному U_я та збурюючому М_с впливах:

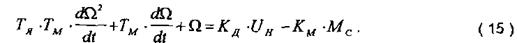
Рівняння (15) у операторній (символічній) формі при нульових початкових умовах:

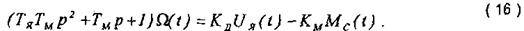
або в операційній формі за Лапласом:

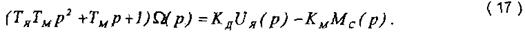
Із (17), використавши принцип суперпозиції, знайдемо передавальні функції двигуна за вхідним та збуруюючим впливами відповідно:

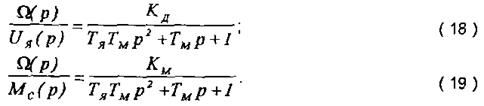
Формули (18), (19) використовуються, коли як вихідний сигнал використовується кутова швидкість W, с^–1.

Якщо вихідним сигналом вважається кут повороту, то необхідно врахувати ще залежність:

де j - кут повороту в радіанах; або в операційній формі:

Згідно з виразами (18), (19), (21), передавальні функції для даного випадку набувають вигляду:

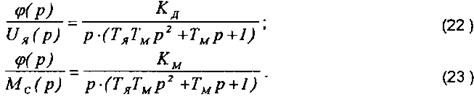
У завданнях, в яких не потрібно враховувати індуктивність якірного ланцюга, передавальні функції (18), (19), при Т_я = 0 можна записати:

2.4.2. Диференціальне рівняння генератора постійного струму з незалежною обмоткою збудження і активним навантаженням

Регульованою величиною (вихідною) для генератора (Рис.2.) є напруга U_г на його затискачах. За вхідну (задаючу) величину у даному прикладі взято напругу обмотки збудження генератора U_з.

Зробимо наступні припущення, що спрощують задачу:

1) кутова швидкість обертання якоря W постійна;

2) гістерезіс відсутній;

3) температура обмоток не змінюється;

4) реакція якоря скомпенсована;

5) індуктивність обмотки якоря L_я = 0;

6) характеристика холостого ходу генератора, залежність ЕРС генератора Е_г - від ампервитків обмотки збудження лінійна:

Е_г = b·І_в·w_в, (26)

де b - коефіцієнт пропорційності, який залежить від характеристики Х.Х. генератора Е_г = f(І_вw_в);

7) навантаження генератора R_н - чисто активне. Рівняння обмотки збудження:

де U_в, І_в, R_в, L_в - відповідно напруга, В; струм, А; опір. Ом; індуктивність, Гн обмотки збудження генератора.

Розділимо обидві частини виразу (27) на R_з, отримаємо:

де Т_в - стала часу обмотки збудження генератора, с;

Згідно з прийнятою кривою XX генератора (26):

Підставивши значення І_з з (30) у (28), одержимо:

Після перетворень і прийнятих позначень рівняння набуде вигляду:

Рівняння для ЕРС якоря ланцюга генератора:

де І_я, U_я - струм, А; опір якоря генератора, Ом;

R_н - опір навантаження, Ом.

Приймаючи:

І_яR_н = U_г (35)

де U_г - напруга навантаження, В.

Одержимо:

U_г = Е_г – І_я R_н (36)

Рівняння (32), (36) запишемо в операційній формі для нульових початкових умов, а саме:

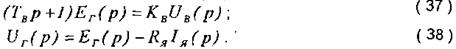
Із врахуванням (37) передавальна функція генератора

при умові, що навантаження відсутнє.

Рівняння (38) враховує збурюючий вплив (струм навантаження І_я).

2.4.3. Диференційне рівняння магнітного підсилювача МП

Виведемо рівняння для найпростішого випадку:

1) маємо одну обмотку керування;

2) крива намагнічування ідеальна: нехтуємо гістерезисом, вважаємо, що працюємо на лінійній ділянці:

3) відсутні зворотні зв'язки;

4) навантаження активне.

Приймаємо для ідеальної кривої намагнічування рівність намагнічуючих сил робочих обмоток і обмоток керування:

У цьому рівнянні: І_к, І_навант – середнє значення струмів керування і навантаження;

w_к - число витків обмотки керування;

w - число витків обмоток генераторного струму з урахуванням їх сполучення.

У перехідному процесі при прикладенні до обмотки керування ступінчастого сигналу для ланцюга керування можна записати:

де і_к - струм в обмотці керування;

r_к - опір обмотки керування;

Ф - потік в обмотці змінного струму.

Проінтегруємо вираз (41), отримаємо за півперіоду змінного струму:

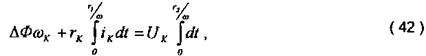
Ділимо всі члени на Dt = r₁/w. потім прийнявши і_к = І_к.ср, напишемо:

Для перехідного процесу довжина якого в багато разів більша r₁/w, можна відношення приростів замінити похідною.

Диференціал потоку dФ зв'язаний, з диференціалом вихідної напруги наступним співвідношенням:

де f - частота мережі живлення.

Середнє значення напруги керування:

Підставивши (44) в (43), отримаємо:

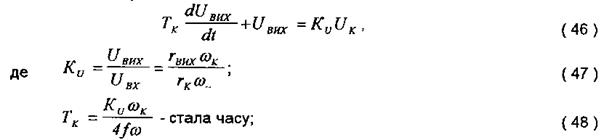
U_вих, U_к – середнє значення напруг на опорах r_вих і r_к.

Передавальна функція:

2.4.4. Передавальна функція тиристорного перетворювача

Перед тим як описувати динамічні властивості тиристорного перетворювача, слід чітко уявити його роботу, згадати можливі схеми включення перетворювачів, їх характеристики. Слід пам'ятати, що тиристорний перетворювач складається з двох основних частин: силової частини СЧ - вентильної групи і системи імпульсно-фазового керування (СІФК) Рис. 3.

Вхідним сигналом перетворювача є величина - керуюча напруга постійного струму U_к. За вихідну (регульовану) величину слід приймати ЕРС перетворювача. СІФК виконує функцію перетворення аналогового керуючого сигналу в відкриваючі тиристори імпульси. Потрібно чітко уявляти, що електричною вихідною величиною СІФК є імпульс, а функціональною - кут відкривання тиристорів a. Ці величини є вхідними для силової частини перетворювача, його вентильної групи ВГ.

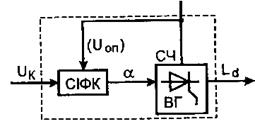
Рис. 3. Структурна схема тиристорного перетворювача

Як відомо, широкий вжиток в сучасних СІФК знайшов вертикальний принцип керування. Кожний блок керування містить в собі генератор пилкоподібної напруги ГПІ, який синусоїдальну форму опорної напруги U_оп перетворює у пилкоподібну (Рис. 4.). Ця напруга порівнюється з регульованою напругою U_к і в момент їх рівності генератор імпульсів ГПІ видає відкриваючий імпульс на тиристор.

Зміна U_к приводить до зміни фази імпульсу (Рис. 5).

У курсовій роботі з ТАК студент повинен, базуючись на знанні динамічних властивостей перетворювача, скласти передавальну функцію, вказавши на допуски які ним були при цьому зроблені.

Рис. 4. Структурна схема блока керування Рис. 5. Регулювання фази імпульса по тиристором, вертикальному принципу

керування.

Силова частина перетворювача може розглядатися як безінерційна ланка. На відміну від силової частини перетворювача СІФК може вносити значні фазові зсуви величини а відносно керуючої напруги. Вони визначаються інерційністю елементів які входять в склад СІФК.

З урахуванням інерційності СІФК передавальна функція перетворювача для лінійної ділянки його характеристики керування має вигляд:

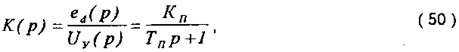
де Т_п = 0,01 + 0,02 – стала часу, с;

е_d - середнє значення ЕРС перетворювача, В;

К_п - коефіцієнт підсилення перетворювача за напругою.

Оскільки інерційність перетворювача мала, то її враховувати має сенс для малоінерційного навантаження, сталі часу якої рівні з величиною сталої часу ТП. Прикладом такого навантаження є двигун постійного струму з незалежним збудженням. Для навантаження з більшою індуктивністю, наприклад, обмотки збудження, інерційність перетворювача не враховується в розрахунках.

2. 4. 5. Передавальні функції операційного підсилювача

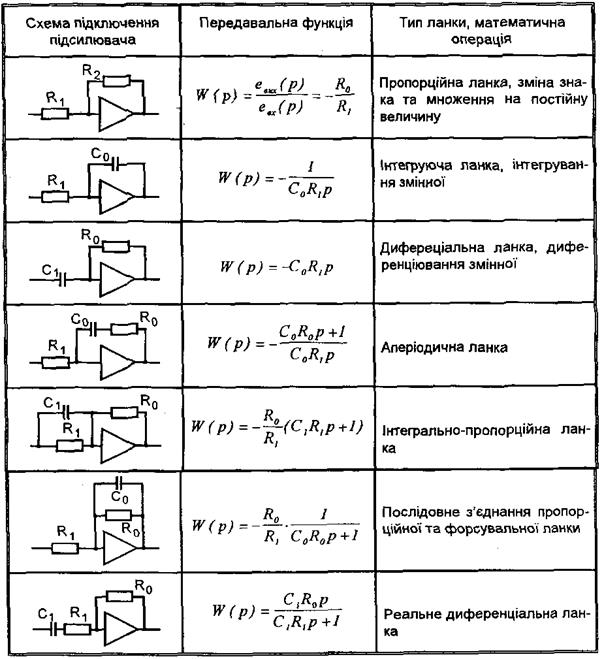
Операційні підсилювачі ОП виконують функціональне перетворення керуючого сигналу, відповідні певним математичним операціям: пропорційній зміні, інтегруванню, інтегрально-пропорційному, диференціально-пропорційному перетворенням. ОП в АСК використовується як корегувальні ланки.

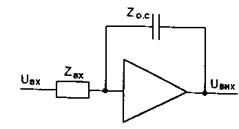
Рис. 6. Принципова схема операційного підсилювача

Для отримання необхідного функціонального перетворення керуючого сигналу в ОП використовуються зворотні зв'язки. Для отримання передавальної функції ОП можна скористатися схемою Рис. 6. Передавальна функція ОП відносно одного входу має вигляд:

де Z_оп(р) - операторний опір зворотного зв'язку;

Z_вх(р) - операторний опір ввімкнений на вхід підсилювача. У таблиці 1 наведені передавальні функції, схеми сполучення СК.

Наведені у таблиці 1 передавальні функції отримані в припущенні ідеальної передачі сигналу, коли коефіцієнт підсилення К_оп = ¥ і перешкоди, що супроводжують корисний вхідний сигнал а також дрейф нуля відсутні.

2. 4. 6. Передавальна функція тахогенератора

В усіх початкових схемах завдання на курсову роботу для систем стабілізації швидкості в якості датчиків швидкості використовуються тахогенератори постійного струму ГГГ). Вхідна величина ТГ - кутова швидкість W, вихідна - напруга U_вих, що видається на опір навантаження R_нав.

При складанні передавальної функції ТГ слід знехтувати:

1) індуктивністю якірного ланцюга;

2) моментом інерції;

3) реакцією якоря;

4) нелінійністю статичної характеристики в зоні малої швидкості;

5) пульсаціями напруги;

6) зміною магнітного потоку.

Таблиця 1. Схеми увімкнення, передавальні функції операційних підсилювачів

Знайдемо передавальну функцію тахогенератора.

Оскільки:

К_тг - передавальний коефіцієнт ТГ, В·с/рад;

К- конструктивна стала;

Ф - магнітний потік збудження, Вб;

R_тг - опір якірної обмотки і щіточного контакту, Ом.

Передавальна функція тахогенератора:

В окремих завданнях для зниження пульсацій до виходу ТГ підключений конденсатор ємністю С. При цьому передавальна функція ТГ набуває вигляду:

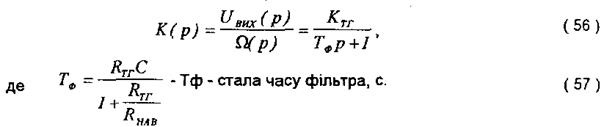
2.4.7. Рівняння і передавальна функція датчика розузгодження

У завданнях на курсову роботу в якості датчика розузгодження ДР у слідкуючій системі використовується схема, що складається з двох сельсинів, що працюють в трансформаторному режимі.

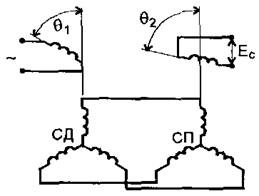
Рис. 7. Схема з'єднання сельсинів в трансформаторному режимі

Схема сполучення сельсинів приведена на Рис.7. Однофазна обмотка сельсина-датчика СД приєднана до мережі змінного струму, а його обмотка ротора з'єднана з обмоткою ротора сельсина-приймача СП. Змінний струм, що живить однофазну обмотку СД, створює пульсуючий потік, який наводить в обмотках фаз ротора ЕРС, які співпадають за фазою, але відрізняються за амплітудою. Струми, що проходять в обмотках ротора СП створюють пульсуючий потік, який наводить ЕРС в однофазній обмотці приймача. Частота цієї ЕРС дорівнює частоті мережі. Значить, СП працює як трансформатор, первинною обмоткою якого є його трьохфазна обмотка ротора, а вторинною - однофазна обмотка статора.

Нижче наведена залежність діючого значення ЕРС Ес однофазної обмотки СП від кута розузгодження роторів сельсинів:

Dq = q₁ - q₂,

де q₁ - кут повороту ротора СД відносно початкового положення при якому вісь першої фази роторної обмотки співпадає з віссю обмотки статора Рис. 7;

q₂ - кут повороту ротора СП відносно початкового положення.

Припускаючи, що діюче значення ЕРС кожної обмотки ротора СД змінюється синусоїдальне в залежності від куга повороту q₁ і враховуючи одинакові параметри сельсинів, отримаємо:

де Е₁, Е₂, Е₃ - діючі значення ЕРС, наведені відповідно в першій, другій і третій фазах ротора,

Е_m - діюче значення ЕРС, наведене в будь-якій з обмоток ротора при співпаданні її вісі з віссю однофазної обмотки.

Відповідно, діюче значення ЕРС кожної обмотки ротора СП слід записати:

де Z - повний опір фази обмотки ротора;

К_т - коефіцієнт пропорційності між струмом і ЕРС.

ЕРС Е_с рівна сумі окремих ЕРС, наведених в однофазній обмотці СП, якщо результуючий магнітний потік розглядати як геометричну суму трьох потоків, створених окремими обмотками ротора СП. Отже:

Підставляючи значення Е₁^/, Е₂^/, Е₃^/, із (59) в (60) і використовуючи (58), отримаємо після відповідних перетворень:

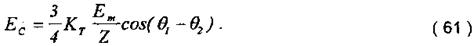
Якщо в початковому положенні вісі роторів сельсинів СД і СП розмістити перпендикулярно, то розузгодження системи визначається як:

Тоді:

Для малих кутів:

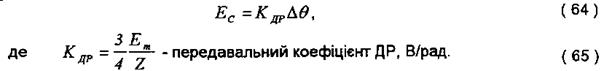
У курсовій роботі ДР слід розглядати як безінерційну ланку, передавальна формула якої:

Потрібно чітко сформулювати прийняті припущення.

2.5. Побудова структурної (алгоритмічної) схеми АСК

Після запису в операційній формі рівнянь окремих елементів АСК і визначення їх передавальних функцій потрібно перейти до побудови структурної (алгоритмічної) схеми системи. При цьому потрібно пам'ятати, що структурна (алгоритмічна) схема представляє собою графічне зображення системи рівнянь динаміки (алгоритмів) елементів, записаних в операційній формі (в вигляді передавальних функцій).

При складанні структурної (алгоритмічної) схеми АСК повинні виконуватися наступні правила:

1) структурна схема повинна обов'язково мати вхідні та вихідні зовнішні впливи, визначені в завданні на курсову роботу;

2) кожен вхідний (задавальний) сигнал, що являється незалежною функцією часу, повинен мати тільки вхід в структурну (алгоритмічну) схему АСК:

3) вихідний сигнал може замикатись в середині схеми і мати вихід в вигляді відгалудження (система замкнена за вихідним сигналом) або не замикатися в середині схеми (система розімкнена за вихідним сигналом):

4) усі внутрішні зв'язки, що визначаються системою рівнянь, повинні мати виходи і входи.

Послідовність складання структурної (алгоритмічної) схеми АСК за заданою системою диференціальних рівнянь її окремих елементів наступна:

1) система диф. рівнянь записується в операційній формі;

2) для кожного рівняння системи вибирається вхідна та вихідна величини;

3) кожне рівняння записується відносно вихідної величини або члену, що має її старшу похідну;

4) будуються графічні зображення кожного диференційного рівняння;

5) складається загальна структурна (алгоритмічна) схема як сукупність графічних відображень кожного диференційного рівняння.

Слід відзначити, що задача побудови структурних (алгоритмічних) схем може вирішуватись неоднозначно, тобто можна дістати кілька варіантів графічного зображення, але після відповідних перетворень усі зображення повинні бути еквівалентними.

За приклад розглянемо складання структурної (алгоритмічної) схеми двигуна постійного струму незалежного збудження при керуванні за ланцюгом якоря, якщо його рух може бути записано системою лінеаризованих рівнянь, наведених в 2.4 цих методичних вказівок (див. рівняння (8), (9)).

Рівняння 9 описує перехідні процеси у ланцюгу якоря двигуна. За вихідну координату приймаємо струм якоря двигуна І_я, а за вхідну - напругу U_я і проти-ЕРС двигуна:

Е_д = КФW

тоді (9) після перетворень слід записати у вигляді:

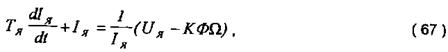
або в операторній формі для нульових початкових умов:

Рівняння (8) слід привести до вигляду:

І_с - статичний струм навантаження, що дорівнює:

Далі слід записати вираз (69) в операційній формі для нульових початкових умов:

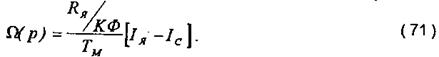
Структурна (алгоритмічна) схема, що відповідає рівнянням (68) І (71), приведена на рис.8.

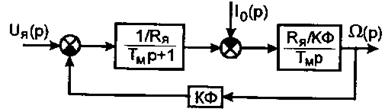
Рис. 8. Структурна (алгоритмічна) схема двигуна постійного струму з незалежним збудженням

2.6. Розрахунок коефіцієнтів передачі і постійних часу електроприводу

Передавальні коефіцієнти К_д і К_м, з (13) і (14) п. 2.4.1. цих методичних вказівок, слід визначити за даними каталогу для обраного двигуна. К_д можна визначити з рівняння:

де U_н, І_н - номінальні напруга і струм якоря двигуна;

W_н - номінальна кутова швидкість двигуна, рад/с;

n_н - номінальні оберти двигуна, об/хв.

К_м можна визначити згідно (14), знаючи КФ і І_я.

Електромеханічну постійну часу визначаємо згідно з виразами (7) і (11) (п- 2-4.) користуючись (72) і знаючи момент інерції двигуна, опір ланцюга якоря R_я, Ом.

Для знаходження числового значення електромагнітної постійної часу якірного ланцюга двигуна (12), індуктивність якірного ланцюга двигуна слід знайти за формулою:

де р - число пар полюсів;

К_L = 5-6 – для компенсаційних машин.

2.7. Визначення передавальних функцій АСК без корегувальної ланки

У даному розділі курсової роботи потрібно визначити наступні передавальні функції АСК:

1) розімкненої системи К_р(р);

2) замкненої системи за задавальним впливом К_з(р);

3) замкненої системи за збурюючим впливом – К_f(р);

4) за помилкою від задавального і збурюючого впливу - відповідно К_ef(р) і К_e(р). Передавальні функції слід визначати за структурною (алгоритмічною) схемою заданої АСК.

Приступаючи до складання передавальних функцій АСК, необхідно, перед усім повторити правила перетворення структурних (алгоритмічних) схем та навчитися користуватися ними:

Таблиця 2. Правила перетворення структурних (алгоритмічних) схем

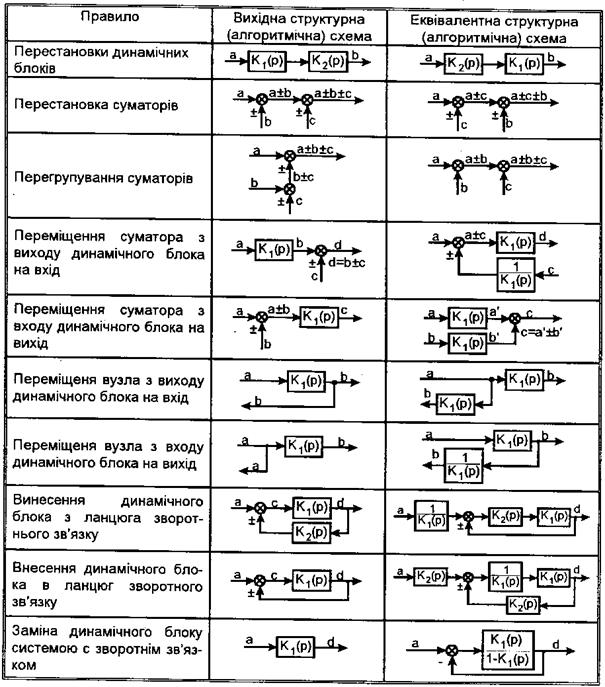
1. Замінити групу послідовно і паралельно з'єднаних ланок, а також ланок із зворотним зв'язком, однією еквівалентною ланкою з передавальною функцією К _е (р). Передавальні функції вказаних типових з'єднань направленої дії описуються виразами:

де n - кількість ланок;

К_п(р) - передавальна функція ланки у прямому ланцюгу;

К_зз(р) - передавальна функція ланки ланцюга зворотного зв'язку.

У виразі (76) знак "+" відповідає від'ємному, а ''–" - додатному зворотному зв'язку

2. Перенести вплив з однієї точки системи в іншу (суматорів, точок розгалудження) таким чином, щоб можна було вилучити перехрещувані зв'язки між контурами. При цьому сигнали на виході системи повинні бути незмінними (табл. 2).

Усі початкові принципові схеми завдання на курсову роботу у результаті структурних перетворень можуть бути зведені до однієї загальної структурної схеми, показаної на рис. 9.

Рис.9. Структурна (алгоритмічна) схема АСК

Тут f - зовнішня збурююча дія;

у - регулююча величина;

х - задавальний вплив;

e - розузгодження;

К_f(р) і К_n(р) - передавальні функції відповідних ділянок замкненої АСК між місцями прикладення збурення f, величини х, що задається і регульованої координати y.

У лінійних системах за наявністю кількох зовнішніх впливів можна кожне з них розглядати незалежно від останніх.

Нижче наводяться передавальні функції замкненої АСК за кожним із впливів:

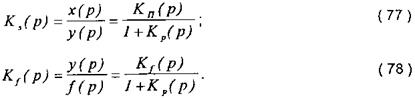
Вирази для передавальних функцій за помилкою:

2.8. Визначення усталених помилок в АСК

Помилка в АСК в усталеному режимі являється одним з показників якості системи і задається в початкових даних на курсову роботу. Студент повинен визначити помилку системи в усталеному режимі за задавальним або збурюючим впливом (залежно від завдання) і порівняти одержаний результат із заданим.

Для визначення помилки АСК потрібно записати передавальну функцію (79) або (80). Для усталених значень, коли час t досить великий, в області зображення це відповідає значенням р = 0. Тому, підставивши у (79) і (80) р = 0 і задавшись вхідним сигналом, знайдемо помилку в усталеному режимі.

2.9. Дослідження системи без корегувального пристрою на стійкість

Дослідження АСК на стійкість можна проводити будь-яким відомим способом, обгрунтовуючи при цьому вибір того чи іншого способу дослідження. Але якщо в завданні на розрахунок передбачена побудова логарифмічних характеристик, то доречно аналіз стійкості проводити за ними. У зв'язку з цим необхідно зупинитися на деяких питаннях, зв'язаних з побудовою логарифмічних характеристик.

Перед усім, слід звернути увагу на правильність побудови структурної схеми розімкненої системи. Нагадаємо, що передавальна функція розімкненої системи, за якою будуються логарифмічні характеристики, повинна мати передавальні функції усіх ланок, що входять до замкненої системи, а також і передавальні функції зворотних зв'язків. Тому, коли зображується структурна (алгоритмічна) схема розімкненої системи, необхідно пам'ятати, що розрив робиться тільки по лінії головного зворотного зв'язку таким чином, щоб між входом системи і місцем розриву не було ніяких ланок. При цьому місцеві зворотні зв'язки, що охоплюють окремі ланки або групи ланок, не розриваються; що приводить до незручної для логарифмування форми.

Для того щоб у цьому випадку використовувати звичайні методи побудови асимптотичних логарифмічних характеристик, необхідно ланку ланцюга з місцевим зворотнім зв'язком розглянути як замкнений контур, знайти його передавальну функцію і привести її до вигляду, зручного для логарифмування, тобто представити передавальну функцію у вигляді добутку типових ланок.

У завданнях на курсову роботу є як статичні, так і астатичні АСК. Якщо АСК складається з безінерційних, аперіодичних і коливальних ланок, то система є статичною. Логарифмічна амплітудно-частотна характеристика ЛАЧХ:

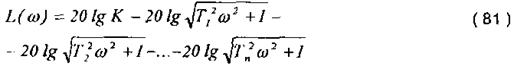
Логарифмічна фазо-частотна характеристика ЛФЧХ:

З виразу (81), (82) видно, що ЛАЧХ і ЛФЧХ розімкненої системи відповідно рівні сумі ЛАЧХ і ЛФЧХ окремих ланок.

Слід ознайомитися із логарифмічними частотними характеристиками динамічних ланок. Однак при побудові її зручніше будувати як результуючу ЛАЧХ всієї системи.

Приступаючи до побудови результуючої ЛАЧХ, необхідно чітко представити методику її побудови.

Розглянемо побудову ЛАЧХ для випадку, коли система складається з трьох аперіодичних ланок і однієї безінерційної.

Припустимо, що Т₁ < Т₂ < Т₃. Побудову потрібно починати з визначення частот спряження:

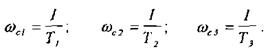
Потім необхідно відкласти ці частоти на вісі абсцис і провести через точки w_с1, w_с2, w_с3 пунктирні вертикальні лінії (рис. 10). При побудові потрібно пам'ятати, що ЛАЧХ у області низьких частот визначається тільки безінерційними ланками в статичній системі, безінерційними і інтегруючими ланками в астатичній системі (якщо в системі немає диференціюючих ланок).

Побудову результуючих характеристик завжди слід починати з області низьких частот, У даному випадку будується характеристика безінерційних ланок з коефіцієнтом підсилення К. Цю характеристику потрібно провести на рівні 20lg К до першої спряжуючої частоти w_с1 Потім, починаючи з w_с1 і далі, відкладається високочастотна асимптота першої аперіодичної ланки.

Рис.10. ЛАЧХ розімкненої статичної системи

Тому нахил прямої на ділянці w_с1 – w_с2 дорівнює -20 дБ/дек, Починаючи з частоти w_с2, нахил збільшується ще на -20 дБ/дек, так як зараз впливає високочастотна асимптота другої інерційної ланки.

Таким чином, при наявності у статичній системі лише безінерційних і аперіодичних ланок, нахил прямої в області низьких частот дорівнює 0 дБ/дек, після n-ної спряжуючої частоти n20 дБ/дек (у розглянутому прикладі -60 дБ/дек).

Побудована описаним вище способом результуюча ЛАЧХ приведена на рис.10. Комплексна передавальна функція розімкненої астатичної системи за наявністю однієї інтегруючої ланки і n аперіодичних ланок має наступний вигляд:

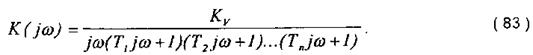
Методика побудови ЛАЧХ лишається такою самою, як і для статичної системи. Тільки в області низьких частот в астатичній АСК результуюча ЛАЧХ обумовлюється сумою ЛАЧХ безінерційної і інтегруючої ланок. Тому ЛАЧХ системи з астатизмом першого порядку в області низьких частот має нахил, що дорівнює -20 дБ/дек.

На рис. 11 приведений приклад побудови ЛАЧХ астатичної системи з астатизмом першого порядку для випадку n = 2.

Побудова виконана вважаючи, що 1 < Т₁ < Т₂.

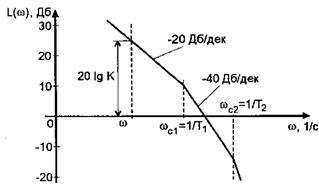
Рис. 11. ЛАЧХ розімкненої системи з астатизмом першого порядку

ЛФЧХ слід будувати як суму фазових характеристик окремих ланок, кожна з яких може бути обрахована як відношення уявної і дійсної частин, тобто:

Ці характеристики можна будувати за допомогою шаблона.

Приклад побудови ЛАЧХ і ЛФЧХ розімкненої одноконтурної системи з передавальною функцією приведений на рис. 12.

Побудувавши ЛЧХ, слід визначити запас стійкості за фазою як рівність між 180^о і абсолютним значенням аргументу комплексної передавальної функції при частоті зрізу, тобто:

Запас стійкості за амплітудою DL визначається як число децибел, на яке потрібно збільшити підсилення системи, щоб система досягла межі стійкості.

Визначення запасу стійкості за амплітудою і за фазою показано на рис.13.

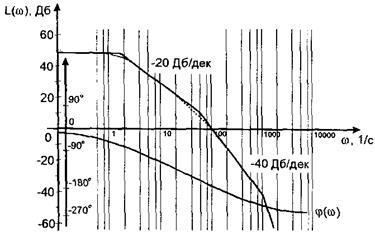
Рис. 12. ЛАЧХ розімкненої статичної системи з коефіцієнтом підсилення К=250 і постійними часу інерційних ланок

Т₁ = 0,7с; Т₂ = 0,02 с; Т₃=0,0015 с.

– запас стійкості за амплітудою     – запас стійкості за фазою

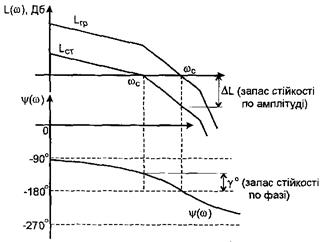
Рис. 13. До визначення запасу стійкості за амплітудою та фазою

Якщо система виявилась нестійкою, то необхідно передбачити заходи з її стабілізації.

Питання стабілізації системи, а також одержання заданих показників якості вирішується у наступному розділі через синтез корегуючого пристрою.

2.10. Вибір корегуючого пристрою із умов заданих показників якості АСК

2.10.1. Постановка задачі і загальний порядок синтезу корегувального пристрою

Автоматичні системи керування, звичайно не мають потрібної якості. Для забезпечення необхідних властивостей у їх основний контур вводять корегувальний пристрій КП.

У даному розділі курсової роботи студент повинен розв'язати задачу синтезу корегувального пристрою. Ця задача полягає в тому, щоб при початковій схемі АСК що маємо структура і параметри якої відомі, визначити передавальну функцію, вибрати принципову електричну схему і розрахувати параметри корегувального пристрою, увімкнення якого до системи забезпечить отримання заданих показників якості: величини перерегулювання s%, час регулювання t_p, статичну похибку e_ст.

У замкненому контурі системи КП може бути включений або послідовно з функціонально необхідними елементами (між вимірювальними і виконавчими), або паралельно з ними (у вигляді зворотних зв'язків, охоплюючих найбільш інерційні елементи). У зв'язку з цим розпізнають два основних метода корекції АСК: метод послідовної корекції і метод паралельної корекції і два типа корегувальних пристроїв - послідовні і паралельні. Із корекцією АСК за допомогою послідовних і паралельних пристроїв постійного струму рекомендується ознайомитись в літературі.

Для конкретних АСК, обумовлених завданням на курсову роботу, в якості корегувального пристрою потрібно використовувати послідовні КП.

У курсовій роботі синтез послідовного КП рекомендується здійснювати за допомогою логарифмічного частотного методу, так як вказаний метод є найбільш простим, наглядним, часто використовується при інженерних розрахунках.

Ідея методу логарифмічних частотних характеристик ЛЧХ базується на зв'язку перехідної функції h(t) з частотною характеристикою ДЧХ замкненої системи – Р_з(w) і Р_з(w) з логарифмічною амплітудно-фазовою частотною характеристикою (ЛАФЧХ) розімкненої системи. Дякуючи вказаному зв'язку можна за заданими показниками якості АСК (s%, t_р, e) будувати бажані ЛЧХ.

Під бажаною ЛЧХ слід розуміти таку частотну характеристику системи, при якій забезпечуються задані показники якості АСК.

Завданням на курсову роботу передбачені тільки мінімально-фазові системи, тобто системи, у яких передавальні функції не мають правих нулів та полюсів, є однозначний зв'язок між амплітудою і фазо-частотними характеристиками. Тому про перехідний процес таких АСК можна судити тільки за ЛАЧХ.

Студент повинен самостійно ознайомитися з питаннями обґрунтування можливості використання частотних характеристик АСК для побудови перехідної характеристики h(t), з приблизною оцінкою показників якості перехідного процесу за ДЧХ замкненої системи, з номограмами для визначення ДЧХ за ЛЧХ розімкнених систем, за підручнику.

Загальний порядок синтезу корегувального пристрою АСК наступний.

1. Будуємо ЛАЧХ початкової незкорегованої системи з урахуванням заданого коефіцієнта підсилення розімкненої системи К_р. Для цього необхідно визначити К_р. з умови отримання помилки в усталеному режимі не вище заданої, знайти спряжуючі частоти і побудувати ЛАЧХ незкорегованої системи.

2. На цей же графік на основі заданих показників якості (перерегулювання s%, часу керування t_р.макс, помилки в усталеному режимі e) із урахуванням ЛАЧХ початкової незкорегованої системи наносимо бажану ЛАЧХ L_ж(w).

3. Вираховуванням із ординат бажаної ЛАЧХ ординат ЛАЧХ початкової незкорегованої системи визначаємо ЛАЧХ корегувального пристрою L_к(w) за відповідним записом:

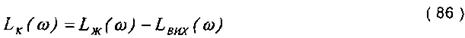
4. За отриманою ЛАЧХ корегувального пристрою знаходимо передавальну функцію корегувального пристрою і підбираємо найбільш простий спосіб його реалізації. Визначаємо параметри КП та його ЛАЧХ.

5. Якщо ЛАЧХ вибраного КП буде декілька відрізнятися від розрахункової, то слід побудувати ЛАЧХ з урахуванням ЛАЧХ реального КП і визначити її показники якості процесу керування.

Найбільш важким етапом при синтезі є побудова бажаної ЛАЧХ.

2.10.2. Порядок синтезу послідовного корегувального пристрою і побудова бажаної ЛАЧХ системи

Порядок синтезу корегувального пристрою та методику побудови бажаної ЛАЧХ розглянемо на прикладі. Нехай комплексна передавальна функція не скорегованої системи у розімкненому стані:

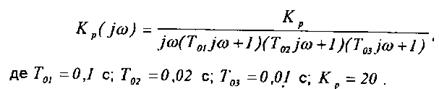
Потрібно забезпечити такі показники якості: при кутовій швидкості обертання ведучого вала a = 36 об/с швидкісна похибка системи не повинна перевищувати 0,18^о, тобто e_уст(t) £ 0,18°; перерегулювання s% < 30%, часу регулювання Т_р.макс £ 0,8 с.

Рекомендується прийняти наступний порядок синтезу.

1. Визначити потрібний коефіцієнт підсилення розімкненої АСК К_р, при якому забезпечується задана точність в усталеному режимі:

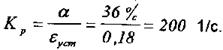
2. Побудувати ЛАЧХ незкорегованої системи з урахуванням коефіцієнта К_р. Для цього потрібно знайти і спряжуючі частоти:

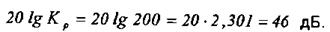
Відкласти при w = 1 ординату L(w = 1) = 20lg K = 46 дБ і через точку цієї ординати провести низькочастотну асимптоту з нахилом –20 дБ/дек до w₀₁ = –20 с^–1.

При w₀₁ змінити нахил на -20 дБ/дек і т. д. ЛАЧХ незкорегованої системи зображена ламаною L(w) на рис. 14.

3. Побудувати бажану ЛАЧХ. Для цього її потрібно розбити на три ділянки: низькочастотна, середньо-частотна та високочастотна. Найбільш важливою є середньо-частотна ланка, тому що вона визначає стійкість та показники якості перехідного процесу.

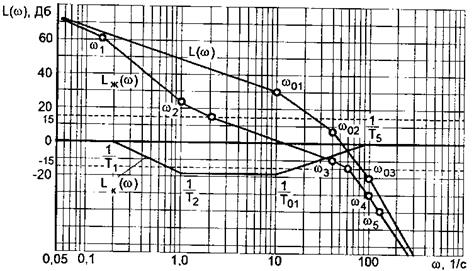
Рис. 14. До синтезу послідовного корегувального пристрою

Для побудови середньо-частотної частини бажаної ЛАЧХ,
потрібно:

3.1. Визначити максимальне значення ДЧХ Р_макс за кривою s_макс% = f(P_макс) рис. 15.

Мінімальне значення ДЧХ відповідно формулі (6.3):

Р_макс » І – Р_макс.

Для прикладу, що розглядається при заданих s_макс% = 30%, Р_макс = 1,3, Р_мін = 0,3.

3.2. Визначити частоту додатного значення w_n, при якій дійсна частотна характеристика перетинає вісь частот, виходячи із заданих і t_р.макс та s_макс%. За знайденим значенням Р_макс, використавши залежність:

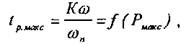
рис. 15, визначити К, а потім, знаючи t_р.макс, знайти частоту додатності:

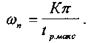
Для розглядуваного прикладу Р_р.макс(w) = 1,3. Згідно кривої t_р.макс = f(Р_макс) К=4. Знаючи t_р.макс, отримаємо:

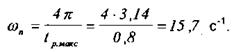
3.3. Визначимо частоту зрізу w_с = (0,6-0,9)w_n. При виборі w_с слід пам'ятати, що чим більша w_n, тим більш швидкодіючою буде система та простіший корегувальний пристрій.

Для систем, у котрих типовою ДЧХ є характеристика Р_макс = 1, тобто s_макс% £ 18%, w_с = 0,625 1/с.

3.4. На вісі абсцис через точку, що відповідає w_с, провести пряму з нахилом -20 дБ/дек. Ця пряма буде середньо-частотною асимптотою бажаної ЛАЧХ.

3.5. Визначити запас стійкості за амплітудою L₁, та фазою Dy бажаної ЛАЧХ відповідно із заданим перерегулюванням. Значення L₁, та Dy знаходимо за кривими

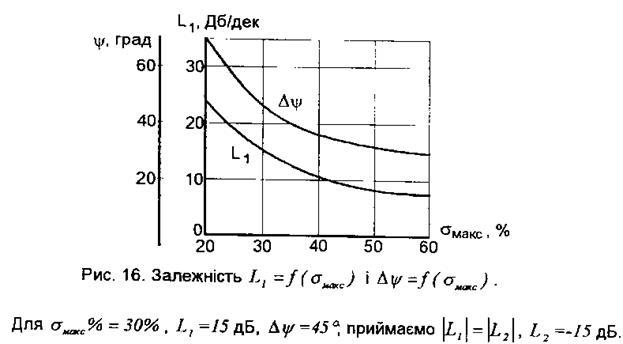
Значення L₁ та L₂ відкласти по осі ординат, і на рівні цих значень провести лінії, паралельні осі абсцис (рис. 14.).

3.6. Оскільки низькочастотний відрізок ЛАЧХ будується з урахуванням К_р і визначає помилки системи в усталеному режимі, за низькочастотну асимптоту бажаної ЛАЧХ слід прийняти низькочастотну асимптоту ЛАЧХ нескорегованої системи з необхідним коефіцієнтом підсилення К_р. При цьому буде досягнута задана точність в усталеному режимі.

3.7. При спряженні середньочастотної асимптоти бажаної ЛАЧХ з низькочастотною слід керуватися такими міркуваннями:

1. Спряження бажано виконувати одним відрізком і йти до того, щоб різниця нахилів асимптот ЛАЧХ нескорегованої системи L(w) і бажаної L_ж(w) ЛАЧХ дорівнювала 20 дБ/дек. У цьому випадку корегувальна ланка буде більш проста. Якщо дістається різниця нахилів асимптот 40 дБ/дек або доводиться проводити спряження більш ніж одним відрізком, то схема КП ускладнюється.

2. Спряження необхідно робити так, щоб у інтервалі частот від w_L1 до w_c, у якому значення ординати бажаної ЛАЧХ знаходяться поміж (L₁ та 0 (L₁(w) ³ L_ж(w) ³ 0) запас стійкості за фазою (надлишок фази) Dy(w) був не менше, ніж запас стійкості Dy, знайдений з умови забезпечення заданого значення перерегулювання, тобто щоб виконувалася нерівність Dy(w) ³ Dy.

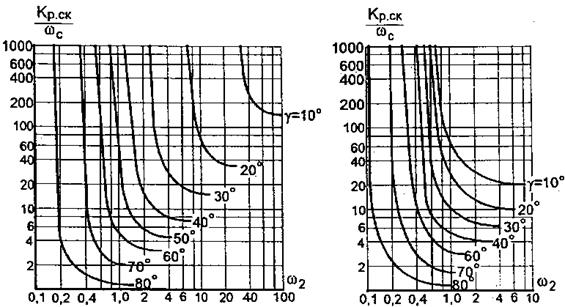
Частоту спряження w₂, (рис. 14), при якій задовольняється ця вимога, знаходять за допомогою номограм (рис. 17).

Щоб визначити w₂, необхідно вирахувати К_рег/w_с, через точку К_ред/w_с на осі ординат номограми провести пряму, паралельну осі абсцис, до перехрещення з кривою, що має індекс g, рівний потрібному запасу стійкості за фазою Dy; з точки перетину опустити перпендикуляр на вісь абсцис і прочитати величину w₂'; вирахувати w₂ за формулою:

Звичайно вимоги до запасу стійкості за фазою задовольняються при w₂ £ w_L1.

3.8. Побудувати високочастотну частину бажаної ЛАЧХ. Вона не сильно впливає на якість, тому її проводять так, щоб різниця нахилів між асимптотами незкорегованої L(w) та бажаної ЛАЧХ L_ж(w) не перевищувала 20 дБ/дек.

Перевірити, чи забезпечується в інтервалі частот від w_с до w_L2, де справедлива нерівність 0 ³ L_ж(w) ³ L₂ необхідний запас стійкості за фазою (Dy = 45°). Для цього потрібно визначити запас Dy_wL2 тільки за частотою w_L2, тобто Dy(w_L2) = 180° = |y(w_L2)|.

Звичайно потрібний запас стійкості за фазою забезпечується, якщо частота спряження w_з» 4 w_с (рис. 14).

а) б)

Рис. 17, Номограми для визначення спряженої частоти бажаної ЛАЧХ при різних нахилах спряжуючої асимптоти: а) -40 дБ/дек; 6) -60 дБ/дек.

4. Визначити потрібну ЛАЧХ L_к(w) корегувального пристрою, яка дістається після вираховування ординат ЛАЧХ L(w) незкорегованої системи з ординат бажаної ЛАЧХ L_ж(w).

5. За виглядом L_к(w), користуючись таблицею, визначаємо передавальну функцію, схему корегувального пасивного контуру та обраховуємо параметри.

У відповідності з отриманою ЛАЧХ L_к(w) комплексна передавальна функція корегувального пристрою:

Потрібною передавальною функцією володіє інтегро-диференціальний КС контур (Рис. 18).

Рис. 18. Інтегро-диференцюючий корегувальний пристрій

2.11. Перевірка показників якості перехідного процесу скорегованої АСК

Перевірку показників якості скорегованої АСК слід виконувати з використанням перехідної характеристики замкненої системи, тобто реакції системи на одиничну ступінчасту функцію 1(t) при нульових початкових умовах.

Необхідно згадати методи побудови перехідної функції АСК, їх переваги та недоліки.

Перевірка включає наступні етапи:

1. Складання структурної (алгоритмічної) схеми замкненої АСК з корегувальною ланкою, передавальна функція та параметри котрої визначені у попередньому розділі методичних вказівок,

2. Визначення за структурною схемі передавальної функції замкненої системи: або за вхідним, або за збурюючим впливом відповідно із завданням.

3. Визначення зображення за Лапласом перехідної характеристики.

4. Розрахунок перехідної характеристики.

5. Графічну побудову перехідної характеристики за отриманими у п.4 даним.

6. Визначення показників якості перехідного процесу (перерегулювання s%, часу керування t_р, с, коливальності N). Для побудови перехідної характеристики АСК слід перед усім записати її зображення.

Передавальна функція замкненої АСК:

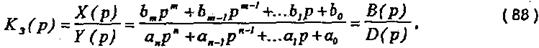
де В(р) - поліном m-ного степеня;

0(р) - поліном n-ного с

Дата добавления: 2015-10-24