Статистическая природа тестовых норм

РЕПРЕЗЕНТАТИВНОСТЬ ТЕСТОВЫХ НОРМ

Статистическая природа тестовых норм

Для того чтобы оценить полученные в результате проведения теста суммарные баллы испытуемого необходимо иметь соответствующие нормы. Тестовые нормы позволяют оценить результат конкретного испытуемого как низкий, средний или высокий. Эти нормы получаются эмпирическим путем в результате проведения испытаний на определенной группе испытуемых. Тесты разрабатываются для применения на определенной популяции – генеральной совокупности (ГС). Наиболее точные нормы получаются при использовании всей генеральной совокупности, но на практике это невозможно. Поэтому обычно используют определенную часть генеральной совокупности – выборку стандартизации. Для того чтобы нормы, полученные на этой выборке можно было применить ко всей ГС, необходимо, чтобы эта выборка была репрезентативной по отношению к ней. Признаки репрезентативной выборки следующие:

Во-первых, она должна быть достаточной по объему. Этот объем зависит от величины генеральной совокупности (но не менее 200 человек).

Во-вторых, она должна по составу соответствовать генеральной совокупности: в требуемой пропорции должны быть представлены испытуемые, относящиеся к разному полу, возрасту, уровню образования, месту проживания и т.п.

Процедура получения тестовых норм заключается в следующем: случайным образом отбираются испытуемые в выборку стандартизации. Затем проводится обследование отобранных испытуемых с помощью нормализуемого теста. Затем для каждого испытуемого вычисляются суммарные баллы.

После этого производится проверка репрезентативности выборки. Первый способ основывается на идее о том, что если взять половину выборки и форма распределения частот суммарных баллов ее совпадет с формой распределения частот целой выборки, то данная выборка репрезентативна по отношению к генеральной совокупности.

Второй способ этой проверки заключается в проверке нормальности распределения в выборке стандартизации, так как большинство психологических переменных имеет нормальное распределение.

Если доказана репрезентативность выборки стандартизации, то для получения тестовых норм вычисляются две статистики:

1) Среднее арифметическое по формуле:

где х_i – суммарный балл по тесту у i-го испытуемого, n – число испытуемых в выборке стандартизации.

2) Стандартное отклонение по формуле

Нормы получаются следующим образом:

Средние нормативные значения для данной выборки испытуемых определяются по формуле

Значения высокие и низкие будут находиться в интервалах соответственно [ ; ] и [ ; ].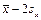

Значения очень высокие и очень низкие будут находиться в интервалах соответственно [ 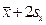; ] и [ ; ].

Значения крайне высокие и крайне низкие – будут находиться в интервалах соответственно > 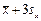и < .

Дата добавления: 2015-10-31