Читайте также:
|
Пусть задано вероятностное пространство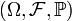 
, и на нём определена случайная величина 
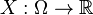. В частности, по определению, 
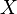является измеримым отображением измеримого пространства 
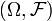в измеримое пространство 
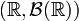, где 
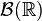обозначает борелевскую сигма-алгебру на 
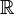. Тогда случайная величина 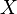индуцирует вероятностную меру 
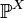на 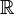следующим образом:
Мера 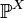называется распределением случайной величины 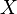. Иными словами, 
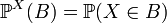, таким образом 
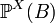задаёт вероятность того, что случайная величина 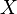попадает во множество 
.
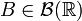Дата добавления: 2015-09-05; просмотров: 34 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Определение | | | Теорема 1 |