|
Читайте также: |
При рассмотрении количества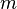 
появлений события 
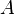в 
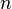испытаниях Бернулли чаще всего нужно найти вероятность того, что 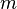заключено между некоторыми значениям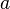и 
и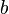 
. Так как при достаточно больших 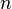промежуток 
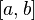содержит большое число единиц, то непосредственное использование биномиального распределения
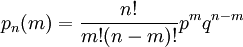
требует громоздких вычислений, так как нужно суммировать большое число определённых по этой формуле вероятностей.
Поэтому используют асимптотическое выражение для биномиального распределения при условии, что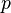 
фиксировано, а 
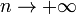. Теорема Муавра-Лапласа утверждает, что таким асимптотическим выражением для биномиального распределения является нормальная функция.
Дата добавления: 2015-09-05; просмотров: 33 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Свойство коэффициента эксцесса | | | Формулировка |