
|
Читайте также: |
N:=1000 -задаем число значений СВ;
i:=0..N-1 -задаем массив индексов;
Xi:=(rnd(1)-0.5) + (rnd(1)-0.5)+ (rnd(1)-0.5)+ (rnd(1)-0.5)+ (rnd(1)-0.5)- с помощью композиции равномерного закона распределения (многократного суммирования rnd(1)-0.5) получаем массив случайных чисел с распределением, близким к нормальному.
Y:=dnorm(X,0,1) Z:=pnorm(X,0,1), где в аргументах (X,0,1) 0-значение математического ожидания, 1-значение среднего квадратического отклонения.
Лабораторная работа № 2
ИССЛЕДОВАНИЕ КАЧЕСТВА ГСЧ СИСТЕМЫ MathCAD И СВОЙСТВ ЧИСЛОВЫХ ХАРАКТЕРИСТИК СЛУЧАЙНЫХ ВЕЛИЧИН
Цель работы: изучение критериев оценки качества датчиков случайных чисел с равномерным распределением по критериям симметричности и независимости и устойчивости числовых характеристик СВ.
Методические указания
Достоинства ГСЧ можно оценить по критерию симметричности в виде отношения значений X, которые больше математического ожидания (МО), к числу значений X < МО, т.е.

Число хh (значений X, превышающих МО) в системе MathCAD вычисляется следующим образом:
Xh:= ∑ if(Xi > MO, 1, 0).
Другой критерий симметричности можно сформулировать в следующем виде

где ME - медиана, представляющая собой такую характеристику сортированного в порядке возрастания вектора случайных величин (с помощью оператора sort(X)), которая делит его на две равные по числу элементов части. Причем одна половина значений больше, а другая - меньше медианы. Если число элементов X1 в векторе нечетно, т.е. N = 2k+l, то

При четном N = 2k медиана равна полусумме двух средних значений
ME:= 1/2 *[x(N-2)/2 + xN/2 ]
Другим критерием качества ГСЧ является независимость (непредсказуемость) случайных чисел, которая может быть оценена с помощью нормированной автокорреляционной функции. Для нахождения значений корреляционной функции необходимо предварительно центрировать значения отсчетов случайной величины, т.е. выполнить операцию
Xi:= Хi - МО.
затем задать область определения функции
М:= 6 t:= О...М
и область суммирования
j:= 0..(N - 1 - М).
После этого корреляционная функция вычисляется по формуле

и рассчитываются значения соответствующей нормированной автокорреляционной функции

ГСЧ считается хорошим (по рассматриваемому критерию), если при t, не равных нулю, |Rt| < 0.1
Порядок выполнения работы
1. Сформируйте массив случайных чисел посредством применения оператора генерации чисел (rnd(1)). Размер массива следует выбирать в пределах от 500 до 1500 чисел. Определите следующие числовые характеристики СВ: математическое ожидание, дисперсию, моду и медиану. Значение медианы должно определяться независимо от четности или нечетности объема выборки.
2. Составьте MathCAD-программу для исследования качества ГСЧ по критериям симметричности Syml и Sym2.
3. Исследуйте качество ГСЧ на предмет независимости случайных чисел, для чего необходимо построить график функции R(T) и определить е максимальное отклонение от нуля при N=1000 и M=50.
4.Оцените устойчивость математического ожидания, дисперсии и медианы к промахам в экспериментальных данных, для чего в векторе X несколько значений замените на явно неправдоподобные и проведите повторные исследования.
5. Сформулируйте выводы, результаты исследований оформите в виде отчета.
Лабораторная работа № 3.
ИССЛЕДОВАНИЕ КАЧЕСТВА ГСЧ СИСТЕМЫ MathCAD ПО КРИТЕРИЮ ПИРСОНА
Цель работы: изучение методики применения критерия Пирсона на примере оценки качества ГСЧ системы MathCAD.
Методические указания
Допустим, мы имеем N случайных чисел в виде вектора X, полученных с помощью ГСЧ (см. лаб. работу № 1):
N:= 100 i:= О..(N-1) Xi= rnd(1).
Равномерность распределения случайных чисел можно оценитьпо критерию Пирсона (æ - квадрат). Для этого сначала строится гистограмма распределения значений X, т.е.:
- определяется число разрядов гистограммы по формуле Стерджесса
I:= ceil(3.3*log(length(X));
- задаются номера границ разрядов гистограммы
К:= О..I;
- находятся максимальное и минимальное значения X
МM:= maх(Х) М:= min(X);
- вычисляются границы подинтервалов гистограммы
intK:= M + К*(ММ - М)/I;
- определяются "эмпирические" частоты попадания отсчетов в разряды гистограммы
W:= hist(int,X).
Определение "теоретических" частот сводится к следующему:
- задаются номера разрядов гистограммы
L:= О..(I - 1);
- вычисляются "теоретические" частоты
FL:= N/I.
Значение критерия Пирсона вычисляется по формуле
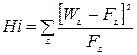
Порядок выполнения работы
1. Составьте MathCAD-программу для исследования ГСЧ на равномерность распределения по критерию Пирсона.
2.Проведите статистическое испытание при значениях объема выборкипорядка 300 - 1500 единиц. Проверьте нулевую гипотезу о равномерном распределении, используя критерий «хи-квадрат» и правостороннюю критическую область. Значение критической точки следует выбрать из таблиц для соответсвующих уровня значимости и числа степеней свободы.
3.Исследуй те, как изменяется значение критической точки в зависимости (а, следовательно, и результат проверки гипотезы) от уровня значимости при зафиксированном объеме выборки. Использовать следующие значения уровня значимости: 0.01, 0.025, 0.05, 0.095, 0.0975.
4.Сделайте вывод о качестве ГСЧ системы MathCAD.
5.Результаты исследований оформите в виде отчета.
Лабораторная работа №4
ПРОВЕРКА СТАТИСТИЧЕСКИХ ГИПОТЕЗ О НОРМАЛЬНОМ РАСПРЕДЕЛЕНИИ
Цель работы: изучение методики применения критерия согласия Пирсона для идентификации нормального закона распределения (проверки гипотезы нормальном распределении).
Методические указания
Известно, что нормальный закон распределения может быть получен композицией равномерных. Для этого можно применить следующий алгоритм: воспользоваться методом многократного суммирования чисел с равномерным законом распределения. При этом MathCAD-программа выглядит следующим образом:
N:= 100 i:= 0..(N-1) K:=Z d:=1..K
Xi:= 
где N - объем выборки; К - число слагаемых (значение параметра К=Z получить у преподавателя); d - номера слагаемых; Х - генерируемый вектор случайных чисел. В зависимости от К получаются различные законы распределения чисел X: К:= 1 - равномерный, К:= 2 - треугольный (Симпсона), К:= 6.или больше шести -- нормальный.
Значение критерия Пирсона вычисляется по формуле
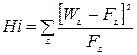 .
.
Значение критической точки определяется по статистическим таблицам исходя из принятого уровня значимости и числа степеней свободы.
Для генерации случайных чисел, имеющих нормальный закон,
Для идентификации необходимо предварительно центрировать и нормировать исходные данные, т.е. проделать следующие операции:
MО:= mеаn(Х) SКО:= stdev(X)
Xi - MO
Xi:= -------.
SKO
Далее требуется построить гистограмму "эмпирического" распределения с равными значениями ширины подынтервалов, что делается в обычном порядке (см. лаб. работу № 3).
После этого необходимо построить гистограмму и вывести значения векторов w и int.
Внимание! Методы идентификации, предусматривающие вычисление статистики æ - квадрат, корректны, если отсутствуют разряды гистограммы, в который попадает меньше пяти отсчетов. В противном случае необходимо объединить разряды с малым числом отсчетов с сoceдними разрядами.
Процедуру объединения при числе разрядов I ≥ 7 можно осуществить автоматически, уменьшив значение I на одну - две единицы, либо вручную, задав в диалоговом режиме более широкими крайние интервалы гистограммы. Последнее, например, при I = 7 делается следующим образом:
- задается число объединяемых разрядов
Т:= 5;
- задается нумерация для модифицированных разрядов и границ
разрядов
q:= 0..T, z:= 0..(Т - 1);
- задаются границы модифицированных разрядов
intmq:=
| int0 |
| int2 |
| int3 |
| int4 |
| Int5 |
| Int7 |
- определяется число отсчетов в модифицированных разрядах
Wm:= hist(intm,X),
которые и будут представлять "эмпирические" частоты.
Далее для вычисления "теоретических" частот можно воспользоваться функцией вероятности, которая имеется в системе MathCAD:
Pz:= N*[cnorm [intmz+1 ] - cnorm[intmz]].
Последующая часть процедуры идентификации аналогична описанной в методических указаниях к предыдущему занятию, с той лишь разницей, что в данном случае число степеней свободы задается формулой n:= Т- 2.
Значение критической точки определяются по соответствующим статистическим таблицам, исходя из уровня значимости и числа степеней свободы.
Порядок выполнения работы
1. Составьте MathCAD-программу для моделирования выборки случайных чисел и проверки гипотезы о ее нормальном распределении по критерию Пирсона.
2.Проведите статистическое испытание при значениях объема выборки. Проверьте нулевую гипотезу о нормальном распределении, используя критерий «хи-квадрат» и правостороннюю критическую область. Значение критической точки следует выбрать из таблиц для соответствующих уровня значимости и числа степеней свободы.
3.Исследуй те, как изменяется значение критической точки в зависимости (а, следовательно, и результат проверки гипотезы) от уровня значимости при зафиксированном объеме выборки. Использовать следующие значения уровня значимости: 0.01, 0.025, 0.05.
4.Сделайте вывод.
Дата добавления: 2015-09-05; просмотров: 105 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Исследование интегральной и дифференциальной функций распределения | | | Оперативный учёт |