Решение. Из рис. 9 видно, что для ответа на вопрос задачи достаточно определить толщину

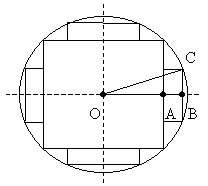
Рис. 5

Из рис. 9 видно, что для ответа на вопрос задачи достаточно определить толщину выпиливаемых досок. Так как сторона квадрата, вписанного в окружность радиуса r, равна r , то ОА = .

Пусть толщина доски АВ = х, тогда ее ширина 2ВС = = , а площадь поперечного сечения:

S(x) = 2 = .

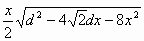Требуется узнать, при каком х из отрезка [0; ] функция S достигает наибольшего значения.

Найдем производную: S'(x) = .

Критическая точка: x₀= Так как S(0) = S , а S(x₀)' > 0, то доски толщиной 0,10d имеют наибольшую площадь поперечного сечения.

Ответ: 0,10d.

Сельское хозяйство и животноводство.

Усилению политехнической и трудовой направленности обучения математике способствует решение задач практического характера. Многие из этих задач сводятся, как известно, к нахождению наибольшего или наименьшего значения функции на некотором промежутке.

Пример

Пастбищные водопоильные желоба для коров иногда устраивают из трех одинаковых досок, сбивая их под некоторым тупым углом величины . Каким должен быть угол 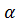, чтобы получился желоб наибольшей вместимости? (рис. 6)

Рис. 6

Дата добавления: 2015-09-05