Первый закон - закон системности: накопление порядка в диссипативных системах сопровождается скачкообразным преобразованием более простых ДС в более сложные.

Термином система именуется совокупность (множество) материальных объектов и законов их взаимосвязи, которая обладает новым свойством, признаком, закономерностью, которой не обладали в отдельности ее составные части. Например, атом кислорода – это система протонов, нейтронов и электронов, которая в соответствии с квантовыми законами и законами электромагнитного и ядерного взаимодействия обладает свойствами вступать в соединение с различными другими атомами, образуя окислы, основания, соли, кислоты, спирты, кетоны, фенолы и многие другие молекулы. Другой набор протонов, нейтронов и электронов также в совокупности с законами микромира формирует атом железа, обладающий совсем другими свойствами.

Степень сложности системы определяется количеством присущих ей закономерностей (свойств, признаков): чем их больше, тем система сложнее.

Система атомов углерода образует новый объект – кристаллы алмаза, обладающие необычайной прочностью, большим коэффициентом преломления света и рядом других свойств, которыми сами атомы углерода не обладают.

Возникновение нового признака, свойства при объединении каких-либо объектов связано с увеличением отрицательной энтропии, информации. Так, согласно [1], энтропия кристаллов четыреххлористого углерода меньше энтропии его газообразного (т. е. хаотического) состояния на 158,27 Дж/моль К, т. е. в 2 раза.

В теории информации уменьшение энтропии при возникновении систем определяется так называемой условной вероятностью [14,15].

Появление нового признака (свойства, закономерности) сокращает неопределенность обнаружения (реализации) данной системы, вследствие этого уменьшается ее энтропия. В [4] этот новый признак назван параметром порядка.

Напомним, что процедура выбора в теории вероятности соответствует процедуре упорядочивания объектов. Понятие порядок и означает возможность быстрого выбора элемента множества. С этой точки зрения понятие "системы" следует связывать с усложнением процедуры определения искомого элемента. Например, если эта процедура включает в себя набор этапов последовательного выбора сначала подмножества, затем подподмножества и т. д. Может быть процедура, соответствующая решению системы уравнений или нелинейного уравнения.. О том, что более сложная процедура выбора интуитивно воспринимается человеком, как более гармоничная система, можно проиллюстрировать следующим примером - рисунок 3.7.

На этом рисунке изображены два квадрата с окружностью в центре. Стороны квадратов разделены на шесть одинаковых отрезков. Концы отрезков пронумерованы от 0 до 6. Одноименные точки правых и левых сторон квадрата соединены направленными слева направо отрезками (1-1, 2-2,...). В зависимости от принципа нумерации получаем два различных рисунка. При этом рисунок 3.7,a, обусловленный простейшей процедурой нумерации точек (сверху вниз справа и слева) воспринимается как менее гармоничный по сравнению с рисунком 3.7,б, у которого правая сторона квадрата пронумерована снизу вверх.

Последовательный переход от одного состояния, характеризуемого набором вероятностей, к другому, если определена процедура перехода, в теории информации именуется марковскими цепями. По сути дела, с помощью этих цепей

А б

Рис. 3.7.Множество линий, соединяющих одноимённые точки сторон квадрата

определяется количественное накопление информации. Еще одним важным принципом формирования систем является симметрия, т.е.сохранение одних признаков при изменении других.

Ниже будут более детально изучены различные виды структур (систем) и основ их формирования.

Вторым законом упорядочивания материи является закон квазиустойчивого сохранения неравновесного состояния.

Устойчивостью называют способность диссипативной системы возвращаться в состояние равновесия после того, как она оказывается выведенной из него сторонними силами.

Лучше всего ее можно проиллюстрировать сравнением двух равновесных моделей – рис. 3.8.

На рис. 3.8,а изображена система, состоящая из лунки (опора) и шарика. Когда шарик лежит на дне лунки, он находится в равновесии - сила его притяжения к земле (вес) уравновешивается реакцией опоры 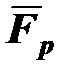. Если шарик сдвигается сторонними (т.е. 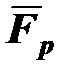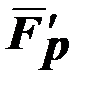не входящими в данную систему) силами вправо или влево от положения равновесия на инфинитезимальный интервал Δх, силы и ^' оказываются направленными друг относительно друга под углом, меньшим 180⁰, – вес – вертикально вниз, а – перпендикулярно поверхности лунки в точке касания с шаром. В результате суммарная сила 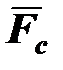направлена так, чтобы вернуть шар в положение равновесия.

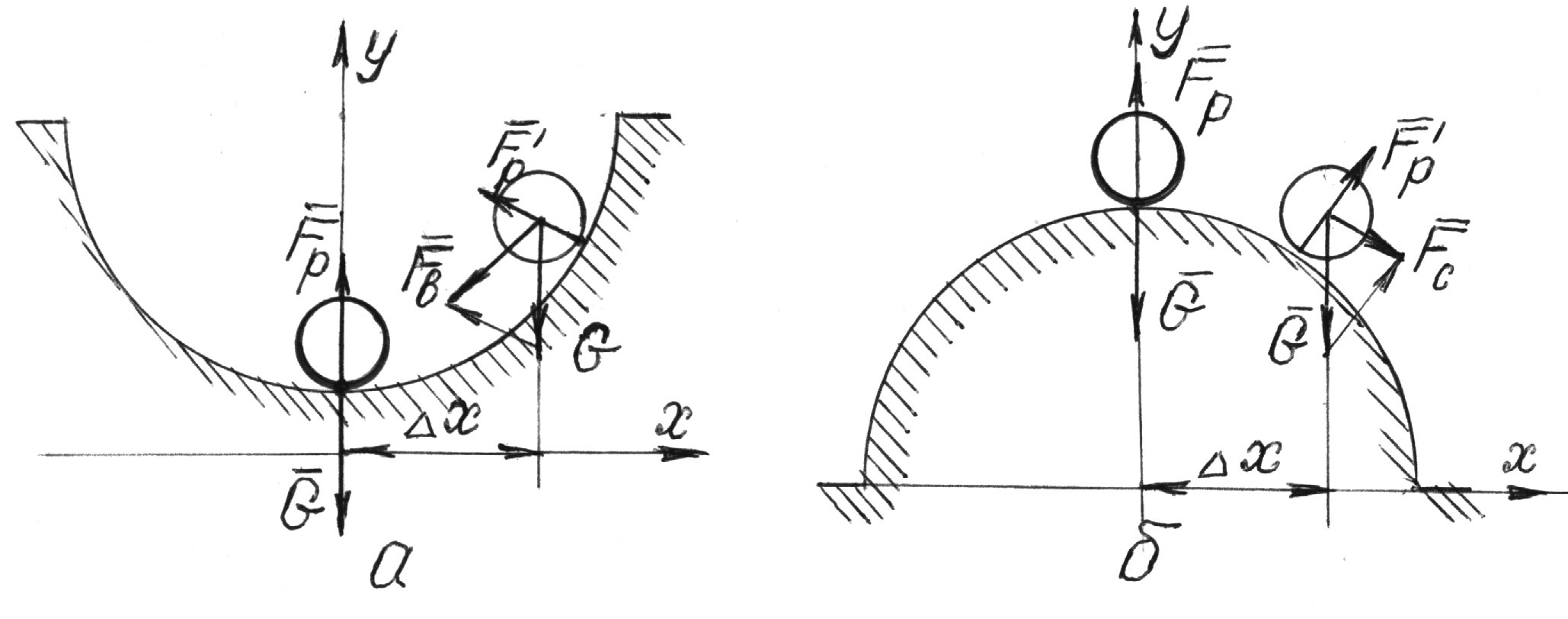
Рисунок 3.8

К объяснению термина «устойчивость»:

а – система «шарик-лунка»(устойчивая); б – система «шарик – бугорок» (неустойчивая).

В случае же, когда система «шар – поверхность опоры» соответствует рисунку 3.8,б (т.е. опора – «бугорок») в аналогичной ситуации возникает результирующая сила , удаляющая шарик от положения равновесия.

Таким образом, система рис.3.8,а – устойчивая, а система рис.3.8,б - неустойчивая.

В общем случае устойчивость определяется кривой изменения координат при движении системы под действием внешних сил вблизи равновесия.

В предыдущей главе было показано, что совместное действие ядерных и электрических сил соединяет протоны и нейтроны в ядре, но одновременно создает предпосылки для распада ядра под действием различных внешних причин. То же самое, но по другим причинам, наблюдается и у более сложных систем - атомов, молекул, кристаллов. Квазиустойчивость обеспечивает сохранение возникших при взаимодействиях простейших видов материи систем, но и одновременно возможность их дальнейших преобразований.

В результате происходит постепенное накопление гармонии во все более сокращающейся области пространства.

Важно определить причины, обеспечивающие устойчивость того или иного объекта и обязательную её ограниченность во времени.

На рисунке 3.9 изображена обобщённая кривая состояния неравновесной системы. На этом рисунке x и y – обобщённые координаты состояния системы, М – изображающая точка системы. Нетрудно видеть, что если какие - либо посторонние причины выведут систему из состояния равновесия (т.е. x₀ изменится на величину 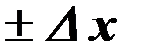), то появляются внутри системы силы, возвращающие её в состояние равновесия. Математическая формулировка понятия устойчивости дана теорией Ляпунова. Здесь лишь отметим, что устойчивость системы вдали от равновесия, т.е. максимума энтропии возможна лишь при наличии особой точки типа впадины в кривой зависимости одного состояния параметра от другого.

Рис. 3.9

Возникновение устойчивого состояния вдали от равновесия.

Ограниченность во времени квазиустойчивого состояния связано с тем, что оно обусловлено термодинамическим процессом передачи тепловой энергии от одного тела к другому. Ясно, что этот процесс ведёт к выравниванию температур и к разрушению порядка в открытой системе.

Таким образом, этот закон также есть закон ограничения существования во времени каждой упорядоченной системы. В течении этого времени количество отрицательной энтропии, как правило, изменяется. Разумеется, в пределах, определяющих основные качества объекта. Это изменение носит обычно горбообразный характер – сначала количество информации накапливается, затем уменьшается. Если на стадии накопления информации произойдет качественный скачок, т. е. возникнет в совокупности с другими объектами новая, более сложная система, то далее процесс изменения информации внутри данного объекта будет всецело зависеть от жизни этого более сложного объекта. Если же объект сохранит свое качество, то дальнейшее течение времени приведет к его разрушению.

Следует подчеркнуть, что в данном параграфе слово "жизнь" употреблено лишь в понимании отрезка времени, в течение которого сохраняется объект сложной конфигурации, а не в смысле способа существования биологических систем, что более правильно.

Ясно, что в природе, т.е. окружающей нас физической реальности, существуют только устойчивые диссипативные системы.

Следует, правда, учесть, что у некоторых систем вследствие инерции возвращение к состоянию равновесия носит колебательный характер – система «проскакивает» состояние равновесия, в ней возникают силы противоположной направленности, вновь пытающийся вернуть ее в состояние равновесия. Система возвращается и снова проскакивает состояние равновесия. И так. далее. В подавляющем большинстве случаев эти автоколебания затухают, и в системе окончательно восстанавливается равновесие.

Однако существуют в природе диссипативные системы, у которых автоколебания не затухают [11]. В этом случае наблюдаются три возможных варианта – 1) амплитуда колебаний раз от раза возрастает и система в конце концов разрушается; 2) возникают устойчивые колебания вокруг положения равновесия, период которых носит случайный, стохастический порядок; 3)возникают устойчивые колебания с постоянным периодом повторения.

Ясно, что первые два варианта свидетельствуют о разрушении системы и, следовательно, она ничем не отличается от неустойчивой. В третьем варианте вновь возникает устойчивость, но не в положении равновесия, а на некоторой динамической траектории вокруг него. К подобного рода системам относят аттрактор [3,4,47].

Явление, связанные, со вторым и третьим вариантами неустойчивости диссипативных систем, именуют детерминированным хаосом.

Правда, во многих случаях, третий вариант незатухающий колебаний можно рассмотреть как новый объект природы, более сложный, нежели исходный – к исходным признакам (закономерностям существования) диссипативной системы добавляется еще один, связанный с этими колебаниями.

Ограниченность во времени устойчивого состояния диссипативных систем связано с тем, что они являются частью открытой системы (см.§3.4). В свою очередь, открытая система существует только в результате термодинамического процесса передачи тепловой энергии от одного тела к другому. Поскольку этот процесс неизбежно ведет к выравниванию температур обоих тел, неравновесная система превращается в равновесную, и генерирование порядка в открытой системе (и, следовательно, в ее части – диссипативной) прекращается. Порядок разрушается и вместе с ним прекращает свое существование диссипативная система.

Таким образом, окончательно закон квазиустойчивости можно сформулировать так: все диссипативные системы устойчивы, но их устойчивость ограничена во времени.

В результате система либо окончательно разрушается, либо становится элементом более сложной системы.

Третьим законом упорядочивания диссипативных систем является закон развития (эволюции) или закон древовидного накопления качества. Суть его в том, что из объектов определенного уровня порядка возникает несколько разновидностей систем более высокой сложности. Однако не все эти более сложные (т.е. с новыми свойствами) объекты могут обеспечить дальнейшее развитие, т.е. образование ещё более сложных систем. При этом под словом развитие (эволюция) подразумевается такое накопление порядка в ДС, которое сопровождается скачкообразным возникновением всё более сложных систем.

Формируется основной ствол развития и побочные побеги. Следует отметить, что эти побочные побеги могут оказывать содействие формированию объектов основного ствола, как положительное (т.е. способствующее ускорению процесса гармонизации), так и отрицательное.

Диссипативные системы, завершающие в данный момент основной ствол развития, отличаются от таковых у побочных ветвей тем, что они лежат в основе формирования еще более сложных систем, в то время, как на последних процесс накопления порядка завершается.

Лучше всего привести пример из химии: атомы элементов образуются из трех видов частиц – электронов, протонов, нейтронов→ в свою очередь из этих атомов образуются молекулы, т.е. сложные соединения→ из этих молекул явно выделяются молекулы органических соединений (соединений, состоящих в основном из углерода и водорода)→ из молекул органических соединений выделяются молекулы аминокислот и нуклеотидов, обладающие одновременно свойствами оснований и кислот и поэтому формирующие сложные полимерные соединения (белки и нуклеиновые кислоты)→ симбиоз определенных белков и нуклеиновых кислот приводит к возникновению циклических реакций (гиперциклов)→ в свою очередь гиперциклы образуют в водной среде микрореакторы, постоянно увеличивающиеся в массе и поэтому делящиеся, →деление микрореакторов ведет к их неограниченному возрастанию в геометрической прогрессии и возникновению конкурентной борьбы между ними и естественному отбору → возникновение живых микроорганизмов (клеток).

Ясно, что все те системы, которые сформировались на каждом из перечисленных этапов, сохраняются, занимая определенную нишу природы. Но при этом они либо не создают более сложных систем, либо создают такие, на которых завершается процесс развития.

Возникновение в процессе постепенного накопления порядка одновременно нескольких вариантов качественно новых систем именуется бифуркацией [1]. Изучение бифуркаций в процессе химических реакций и особенно пространственно-временной диффузии их продуктов – важнейшее направление в деле понимания технологии структурного усложнения объектов природы.

В литературе гуманитарного направления (в частности, в философии) понятие "развитие" включают в понятие "движение"[12]. Следует оговорить, что в естественно-научных дисциплинах движением считают перемещение материальных объектов друг относительно друга, а развитием – накопление отрицательной энтропии, т. е. движение в сфере гармонии (информации).

Надо сказать, что объекты, сформировавшиеся в основном стволе развития, также оказывают влияние на накопление (или разрушение) систем побочных ветвей. Таким образом, формируется сложная единая система, которая воспринимается нами, как природные условия.

Взаимовлияние различных по уровню развития систем приводит к тому, что каждая система с течением времени меняет количество накопленной энтропии. Это обстоятельство обуславливает четвертый закон накопления гармонии в неорганическом мире.

Четвёртым законом накопления порядка в диссипативных системах является закон причинно-следственных связей. Суть его заключается в том, что сложные диссипативные системы образуются из более простых путём причинно-следственных связей. Слова "причина " и " следствие " связывают непосредственно с фактом передачи информации от одного объекта другому. Необходимо отметить, что возможна передача информации (порядка) от нескольких объектов одному или от одного объекта нескольким. Сам процесс передачи может быть непрерывным (аналоговым) или дискретным (цифровым). Причинно-следственные связи приводят к возникновению сложных систем. Полный набор этих связей именуется структурой сложной системы.

Примером объекта, возникающего под воздействием нескольких причин, служит радуга. Ее появление обусловлено сложным взаимодействием солнечных лучей (первая причина) и многочисленных капель дождя (вторая причина).

Примером передачи информации от одного объекта многим служит трансляция какого-нибудь сюжета из телестудии к экранам, расположенным у многомиллионной аудитории телезрителей.

Непрерывной (аналоговой) передачей информации именуется такая, которая состоит из бесконечного числа бесконечно- малых порций, а дискретной (цифровой) – такая, которая состоит из конечного числа конечных порций. Напомним (см.§1.7) что каждая порция информации переносится определенной долей энергии. Ясно, что непрерывная информация переносится бесконечно -большой суммой бесконечно-малых долей энергии, а дискретная – конечными скачками энергии. При этом никакой однозначной взаимосвязи между количеством энергии и количеством информации нет. Более того, строго говоря, бесконечно-малых порций энергии, а, следовательно, и информации не существует. Минимальная доза энергии определяется квантом и соответствует постоянной Планка h [44]. Однако, в теории управления существует теорема Котельникова [45], которая определяет количественную меру информации, позволяющую рассматривать дискретный процесс как непрерывный, Суть ее сводится к сопоставлению количества энергии в порции информации: если первая меньше второй во много раз (это соотношение как раз и вычисляется этой теоремой), то передачу можно рассматривать как непрерывную.

Для изучения структур используют специальные символы [53] – графы. На рисунке 3.7,а показан простейший элемент графа - дуга. Числом x₁ изображается энергия (или какой-либо другой связанный с ней параметр) исходного объекта, x₂ – объекта-следствия, а буквой K – так называемый коэффициент усиления, т. е. отношение x₂ / x₁. В том случае, если объект-следствие создается действием нескольких объектов, граф имеет вид рисунка 3.7,б,

В этом случае:

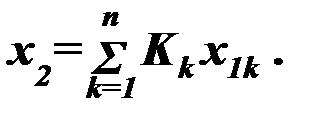(3.6)

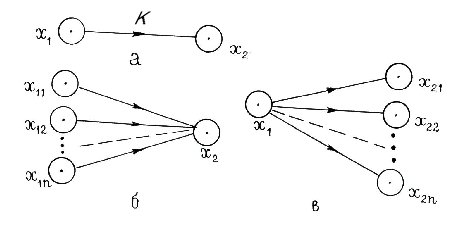
где x₁₁, x₁₂,..., x_1n - исходные объекты (причины), а x ₂ (следствие)– конечны.

Рисунок 3.10

Простейшие причинно-следственные связи:

а – один исток – один сток; б – n истоков – 1 сток;

в – 1 исток – n стоков.

Противоположный случай изображен на рисунке 3.7,в. Объект - причина в теории графов именуется исток, а объект - следствие - сток.

Если энергия на выходе стока x₂ изменяется во времени пропорционально энергии x₁, то порядок (информация) при передаче сохраняется.

Пятым законом накопления гармонии в природе является закон управления. Суть его заключается в том, что во многих случаях гармония сначала возникает в объекте малой энергии, а затем передается объекту большой энергии. Такая передача именуется управлением. Например, процесс кристаллизации охлаждаемой жидкости начинается с возникновения некоторых центров кристаллизации.

При возникновении электрического поля между облаками и земной поверхностью сначала появляются микроскопические объемы ионизации, которые затем вызывают ее лавинообразное протекание в некотором довольно узком канале – молнию.

В химических реакциях роль управляющего объекта играют катализаторы – вещества, понижающие энергию активации молекул и тем самым способствующие возникновению и быстрому протеканию реакции. Этот способ управления особенно важен при создании высших форм организации - биологических систем.

Наиболее наглядно процесс управления иллюстрируется горящей спичкой, поднесенной к бочке с бензином, или пистоном в патроне.

Процесс обратной передачи порядка от объекта большой энергии объекту малой, имеющему бόльший срок жизни, называется запоминанием. Сама информация об упорядоченной энергии, сохраненная в малом объекте, именуется памятью. В дальнейшем эта информация может быть вновь передана объекту большой энергии.

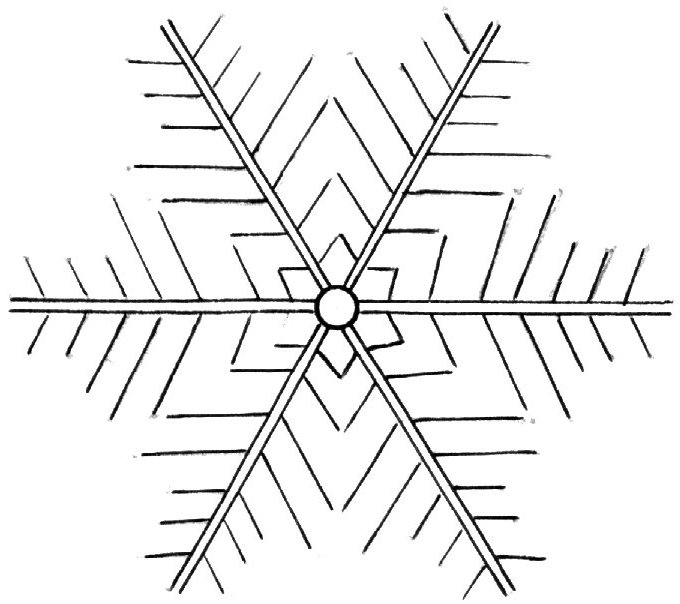
Приведем два примера. Красивая конфигурация кристаллика воды - снежинки (рисунок 3.8) является следствием свойств молекулы воды. Иными словами, в молекуле воды заложена информация о форме кристалла снега. И где бы, когда бы ни превращалась капелька воды в снежинки, конфигурация последних будет одна и та же. Следовательно, молекула воды содержит полную информацию о конфигурации кристалла.

С другой стороны, молекула углерода содержит в себе информацию о таких различных видах кристаллов, как алмаз и графит. В этой молекуле память не детерминирована однозначно, вернее запоминается не только порядок расположения атомов в кристалле, но и условия формирования последнего.

Следует отметить, что в природе возможны и обратные процессы, при которых объект малой энергии вызывает разрушение уже сформировавшегося порядка в объекте большой энергии.

В этом случае также говорят о причинно-следственной связи и даже об управлении, имеющих отрицательный характер. Мы здесь будем относить все четыре введенных термина – управление, память, причина, следствие – только к процессу накопления гармонии.

Рисунок 3.11

Конфигурация кристаллика воды

Отметим, что третий, четвертый и пятый законы являются законами динамики порядка в неорганическом мире. Следует подчеркнуть три обстоятельства: 1) законы накопления гармонии являются элементами самой гармонии; 2) эти законы обуславливают естественный характер процесса создания систем, т. е. позволяют обойтись без понятия сверхъестественного "творца"; 3) эти законы объясняют единство всех процессов в природе и их взаимосвязь.

Дата добавления: 2015-08-27