Дискретизация групповых сигналов

Мы рассмотрели процессы дискретизации сигналов, у которых отношение , условно называемых широкополосными. Несколько по-иному определяется значение частоты дискретизации f _д для сигналов с отношением , которые называются узкополосными. Примерами таких сигналов являются сигналы трехканальной предгруппы с полосой частот 12,3...23,4 кГц, первичной группы с полосой частот 60... 108 кГц, вторичной группы с полосой частот 312...552 кГц и др. систем передачи с частотным разделением каналов.

Будем считать, что импульсные несущие для амплитудно-импульсной модуляции узкополосных сигналов представляют собой периодическую последовательность прямоугольных импульсов (ПППИ) весьма малой длительности. Спектр амплитуд такой ПППИ можно считать равномерным, а интенсивность всех боковых АИМ сигнала - одинаковой. Обозначим произвольную гармонику частоты дискретизации через nf _д Для того, чтобы боковые полосы этой гармоники не совпадали по спектру с исходным сигналом F _H... F _B , необходимо выполнить два условия (см. рис. 1.3):

нижняя боковая НБ-k должна располагаться по оси частот выше или ниже исходного сигнала;

верхняя боковая ВБ-k также должна располагаться по оси частот выше или ниже полезного спектра F _Н... F _B (включая и отрицательные частоты).

Первое условие можно записать в виде двух неравенств, причем безразлично, какое именно из них выполняется

(1.15)

и

(1.16)

Второе условие можно записать в виде двух неравенств, одно из которых обязательно должно выполняться

или (1.17)

и

или (1.18)

Отметим, что условия (1.16) и (1.18) выполняются всегда. Очевидно, что неравенства (1.18) не могут выполняться на практике ни для одного значения k, если F _в> F _н, а выполнение неравенств (1.17) является обязательным для любого значения k. Рассмотрим теперь условия (1.15) и (1.16). Условия (1.16) не могут выполняться для всех значений k. Пусть k1 -максимальное значение k, для которого соотношения (1.16) еще выполняются. Тогда для всех k = k ₁ + 1, должны выполняться условия (1.15). Сказанное можно записать в виде двух неравенств, которые должны выполняться одновременно:

или в другой форме

(1.19)

Очевидно, что выполнение этих условий возможно лишь тогда, когда правая часть больше левой или равна ей, т.е.

Решив последнее неравенство относительно k ₁ получим

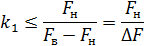
В этом уравнении значение k ₁ может быть любым целым числом в пределах от 1 до 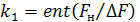Здесь ent (x) означает, что от отношения Fн/ΔF берется только целое число. Из решения неравенств (1.19) и (1.20) можно найти минимально возможную частоту дискретизации f _{д мин}

(1.21)

Нижняя граничная частота дискретизации равна удвоенной ширине спектра дискретизируемого сигнала и достигается лишь в том случае, когда отношение 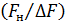является целым числом. В остальных случаях частота дискретизации должна превышать удвоенную ширину спектра исходного сигнала.

Эту методику определения частоты дискретизации полосового сигнала целесообразно применять при Если то частоту дискретизации следует выбирать согласно теореме Найквиста-Котельникова.

Восстановление сигнала из последовательности его отсчетов можно осуществить с помощью полосового фильтра (ПФ). Частота дискретизации при этом выбирается такой, чтобы обеспечить минимальные значения полос расфильтровки ПФ с симметричными или несимметричными характеристиками затухания.

Для иллюстрации вышесказанного рассмотрим пример определения частоты дискретизации для полосового сигнала.

Пример: Требуется определить минимальное значение частоты дискретизации f _Д, сигнала трехканальной предгруппы, для которой F_н = 12,3 кГц и F _в = 23,4 кГц.

Решение. Ширина полосы пропускания сигнала равна Δ F = F _в- F _н = 23,4 - 12,3 = 11,1 кГц. Отношение F _н /∆F= 12,3 / 11,1 = 1, 108. Подставив значения F _н /∆F и F _B в (1.21), получим

Это минимальное значение частоты дискретизации не подходит, так как оно находится в полосе частот дискретизируемого сигнала, что недопустимо. При демодуляции такого АИМ сигнала возможны значительные искажения. Воспользуемся формулой (1.19). Положив в ней k ₁ = 1, получим

(1.22)

Подставив в (1.22) значения граничных частот исходного сигнала, получим: 23,4 < f _д < 2 12,3 = 24,6 кГц. Выбираем значение частоты дискретизации, равное f _д = 24 кГц.

Спектр АИМ сигнала трехканальной предгруппы для f _д = 24 кГц приведен на рис. 1.11.

Рис. 1.11. Спектр АИМ полосового сигнала

Как следует из рис. 1.11,спектр АИМ сигнала состоит из: исходного сигнала 12,3...23,4 кГц; нижней (НБ-1) 0,6...11,7 и верхней боковой (ВБ-1) 36,3...47,4 кГц около первой гармоники частоты дискретизации f _д = 24 кГц; нижней (НБ-2) 24,6...35,7 и верхней боковой (ВБ-2) 60,3...71,4 кГц около второй гармоники частоты дискретизации 2f _д = 48 кГц; нижней (НБ-3) 48,6...59,7 и верхней боковой (ВБ-3) 84,3...95,4 кГц около третьей гармоники частоты дискретизации 3 f _д = 72 кГц и т.д. Демодуляция такого АИМ сигнала может быть осуществлена полосовым фильтром ПФ с симметричной характеристикой затухания (величина полосы расфильтровки слева ΔF_pl = 12,3 - 11,7 = 0,6 кГц и справа Δ F ₉ = 24 - 23,4 = 0,6 кГц равны).

Формула (1.22) с учетом коэффициента k может быть представлена в виде

f _{д =} 2(F н +F в) / (2 k+ 1) (1.23)

Для рассмотренного примера, если k = 1, то из (1.23) следует

f _{д =} 2(F н +F в) / (2 k+ 1) = 2(12,3+23,4)/(2 1+1)=23,8кГц

Всегда значение частоты дискретизации округляется до ближайшего целого кратного 4, т.е. выбираем f _д = 24 кГц. Если частота дискретизации определена по формуле (1.23), то демодуляция АИМ сигнала осуществляется ПФ с симметричной характеристикой затухания, полоса расфильтровки которого равна

(1.24)

Всегда стремятся к минимальному значению частоты дискретизации узкополосного сигнала, что имеет место при k =1.

Соотношения (1.22)-(1.24) для определения параметров дискретизации справедливы при k ≠1 для сигналов, у которых отношение F _в/ F _н<2, т.е. для узкополосных сигналов. Если F _в/ F _н>2, то частота дискретизации определяется из соотношения f _д>2 F _в. Очевидно, что в этом случае для снижения f _д необходимо предварительно осуществить перенос исходного спектра в область более низких частот. Так, для третичной группы с полосой частот 812...2044 кГц частота дискретизации может быть доведена, например, до величины f _д = 2584 кГц. Для этого полосу частот с помощью несущей f _н = 2104 кГц переносим в полосу частот 60... 1292 кГц и далее осуществляем дискретизацию с частотой дискретизации, равной f _д = 2 1292 = 2584 кГц. Снижения частоты дискретизации с помощью преобразования частоты можно получить и для узкополосных сигналов.

Дата добавления: 2015-08-26