Дискретизация или амплитудно-импульсная модуляция

В основе построения ЦСП с ВРК лежит теорема Найквиста-Котельникова, которая гласит: непрерывный во времени сигнал c(t), спектр которого ограничен полосой частот от 0 до FB, полностью определяется последовательностью своих мгновенных значений, которые берутся в точках, отсчитываемых через интервалы времени,

(1.1 а)

или с частотой

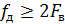(1.1 б)

Процесс преобразования непрерывного во времени и ограниченного по спектру сигнала c(t) в сигнал с(nТ_Д), определенный в точках отсчета Т_Д, 2Т_Д... nT_Д - называется дискретизацией.

Значения сигнала с(nТд) в точках отсчета называются дискретами или отсчетами. Поэтому теорему Найквиста-Котельникова в технической литературе часто называют теоремой отсчетов, а интервал времени между двумя соседними отсчетами называется периодом дискретизации Т_Д.

Рис. 1.1. Дискретизация непрерывного сигнала

Значение теоремы отсчетов состоит в том, что если необходимо передать непрерывный и ограниченный по спектру сигнал с(t), то необязательно передавать его непрерывно, а достаточно передать его отдельные мгновенные значения, взятые через интервал времени Т_д (рис. 1.1).

Между отсчетами сигнала одного канала можно передавать отсчеты сигналов других каналов с теми же параметрами дискретизации. Таким образом реализуется временное разделение каналов.

Процесс дискретизации можно представить как процесс амплитудно-импульсной модуляции (АИМ) сигналом c (t) (рис. 1.1) периодической последовательности прямоугольных импульсов (ПППИ) f ₀(t) с амплитудой Аm, длительностью τ_и и периодом Т_Д или частотой f _д = 1/Т_д (рис. 1.2).

Рис. 1.2. Периодическая последовательность прямоугольных импульсов

Периодическая последовательность импульсов f₀(t) может быть представлена рядом Фурье вида:

(1.2)

где ω_д = 2πF_д - круговая частота дискретизации; А₀, А_k - коэффициенты разложения ряда Фурье, представляющие амплитуду постоянной составляющей и амплитуду k-й гармоники спектра ПППИ соответственно. Амплитуда постоянной составляющей А₀ определяется по формуле:

амплитуды гармоник частоты следования импульсов ПППИ находятся по следующей формуле

Подставив значения коэффициентов разложения А₀ и A_k в (1.2), получим формулу для определения спектрального состава ПППИ:

(1.3)

Модулирующий сигнал c(t) представим в виде:

(1.4)

где Ω_н и Ω_в - нижняя и верхняя граничные частоты модулирующего сигнала соответственно, причем если Ω_н/Ω_в 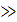2, т.е. модулирующий сигнал является широкополосным.

Амплитудно-импульсный модулированный (АИМ) сигнал можно описать общим для амплитудной модуляции выражением:

f(t) = {l+m_ac(t)}f_Q(t).

Подставив в него c (t) и f _Q(t) из формул (1.4) и (1.3), получим:

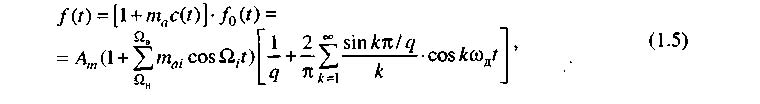
Где 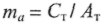- коэффициент глубины модуляции.

Раскрыв скобки в (1.5) и выполнив несложные тригонометрические преобразования, получим

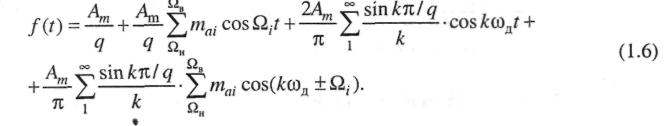
Из выражения (1.6) следует, что спектр АИМ сигнала содержит

- постоянную составляющую с амплитудой Am/q;

- модулирующий (исходный) многочастотный сигнала с амплитудами его частотных составляющих, равными

- гармоники частоты дискретизации - модулируемой ПППИ, амплитуды которых равны

- боковые полосы частот вида 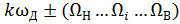с амплитудами

Спектр АИМ сигнала S(ω) представлен на рис. 1.3, где А₀- амплитуда постоянной составляющей; А₁, А₂, A₃, - и т.д. амплитуды первой, второй, третьей гармоник и т.д. гармоник частоты следования импульсов ПППИ или частоты дискретизации; НБ-1 - нижняя боковая полоса частот около первой гармоники частоты дискретизации ω_д — Ω_i, ВБ-1 - верхняя боковая полоса частот около первой гармоники частоты дискретизации ω_д + Ω_i; НБ-2, ВБ-2 - нижняя и верхняя боковые полосы около второй гармоники частоты дискретизации; НБ-3, ВБ-3 - нижняя и верхняя боковые полосы около третьей гармоники частоты дискретизации и т. д.

Демодуляция АИМ сигнала, т.е. выделение модулирующего сигнала, осуществляется фильтром нижних частот (ФНЧ) (рис. 1.3). Это обусловлено наличием в спектре АИМ сигнала исходного сигнала с полосой частот Ω_Н Ω_В. Для реализации ФНЧ необходима полоса расфильтровки (рис. 1.3), которая равна:

Из последнего выражения следует, что частота дискретизации

или или (1.7)

Таким образом, на основе рассмотрения процесса дискретизации как процесса амплитудно-импульсной модуляции получены условия теоремы Найквиста-Котел ьникова

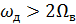_, или , или

Для канала тональной частоты (КТЧ), у которого F_Н = 300 Гц и F_В = = 3400 Гц, частота дискретизации должна удовлетворять условию f_Д > 2F_В = 6800 Гц. Для упрощения и удешевления ФНЧ, необходимых для ограничения полосы частот первичного сигнала перед его дискретизацией в тракте передачи ЦСП, а также в тракте приема для демодуляции АИМ сигнала (восстановления дискретизированного сигнала), необходимо выбрать оптимальное значение полосы расфильтровки ΔF_P. Это значение равно Δ F _P = 1200 Гц. Из (1.7) следует: частота дискретизации f _д = 2 F _в + ΔF_P = 2*3400 + 1200 = 8000 Гц, а период дискретизации Т _д = 1/ f _д = 1/8000= 125 мкс.

Различают амплитудно-импульсную модуляцию первого рода (АИМ-1) и второго рода (АИМ-2). При АИМ-1 мгновенное значение импульсов отсчетов на их длительности τ_и изменяется в соответствии с изменениями модулирующего (дискретизируемого) сигнала. При АИМ-2 значение импульса определяется только значением сигнала в тактовой точке ПППИ (рис. 1.2) и остается постоянной на всей длительности импульса отсчета τ_и. Таким образом, импульсы отсчетов при АИМ-2 имеют плоскую вершину (см. рис. 1.1). При достаточно большой скважности импульсов ПППИ q > 10 сигналы АИМ-1 и АИМ-2 идентичны по спектрам.

Процесс дискретизации (или амплитудно-импульсной модуляции) непрерывного сигнала c (t) сопровождается искажениями дискретизации, обусловленными тем, что действительные первичные сигналы являются ограниченными по времени и, следовательно, имеют неограниченный спектр. Часть этого спектра попадает в полосу частот, выделяемую ФНЧ при демодуляции АИМ сигнала. При дискретизации и последующем восстановлении исходного сигнала происходит его значительное ослабление, так как часть энергии, которая распределена между различными спектральными составляющими АИМ сигнала, подавляется в процессе демодуляции. Как следует из (1.6), амплитуда i-й составляющей сигнала в спектре АИМ сигнала равна

Если C_mi - амплитуда i -ой составляющей на входе АИМ модулятора - дискретизатора, а A_i - амплитуда i - й составляющей на выходе ФНЧ при демодуляции АИМ сигнала, то ослабление в процессе дискретизации равно

(1.8)

Из (1.8) следует, что ослабление растет с увеличением скважности импульсов (числа каналов ЦСП). Это обстоятельство накладывает ограничения на число каналов на этапе дискретизации. Так, если частота дискретизации равна f_Д = 8 кГц или период дискретизации Т_Д = 125 мкс, а τ_и = 4 мкс (что ориентировочно соответствует 30-канальной системе), ослабление сигнала на ступени дискретизации согласно (1.8) будет равно

т.е. полезный сигнал ослабляется почти в 1000 раз. Кроме того, при переходе от АИМ-1 к АИМ-2 (о необходимости этой операции будет сказано ниже) имеют место специфические искажения, для компенсации которых на выходе канала включается амплитудный корректор. Для снижения потерь энергии сигналов при их дискретизации используются усилители низкой частоты, включаемые в тракте передачи и в тракте приема.

Процесс дискретизации, или амплитудно-импульсной модуляции, т. е. формирование канального АИМ сигнала с(nТ_д) осуществляется в индивидуальном АИМ тракте, обобщенная функциональная схема которого приведена на рис. 1.4.

Работа схемы заключается в следующем. На вход АИМ тракта поступает первичный (относительно широкополосный) сигнал c (t). С целью формирования эффективно-передаваемой полосы частот КТЧ и удовлетворения условиям теоремы Найквиста-Котельникова полоса частот первичного сигнала ограничивается фильтром нижних частот (ФНЧ). Далее ограниченный по спектру сигнал поступает на усилитель низкой частоты (УНЧ), предназначенный для компенсации потерь мощности сигнала, обусловленных его ограничением по спектру, процессами дискретизации и преобразования АИМ-1 в АИМ-2. На выходе УНЧ получаем сигнал c (t), параметры которого удовлетворяют условиям его дискретизации на передаче и демодуляции на приеме. С выхода УНЧ сигнал c (t) поступает на канальный амплитудно-импульсный модулятор (КАИМ) или дискретизатор, на другой вход которого с распределителя канальных импульсов поступает ПППИ, следующая с тактовой частотой f_д или с периодом Т_д. На выходе КАИМ получаем дискретный сигнал с(nТ_д) (см. рис. 1.1). Затем N индивидуальных канальных АИМ сигналов объединяются в общий групповой (многоканальный) АИМ сигнал и поступают в тракт передачи ЦСП. На выходе тракта передачи ЦСП из группового АИМ сигнала с помощью канального селектора КС, управляемого ПППИ, поступающей от РКИ, выделяется индивидуальный АИМ сигнал с(nТ _д), соответствующего канала. С помощью ФНЧ осуществляется его демодуляция (см. рис. 1.3). Непрерывный сигнал с выхода ФНЧ поступает на УНЧ, который обеспечивает номинальное значение сигнала c (t) на выходе канала.

Процессы дискретизации, демодуляции и временного разделения каналов иллюстрирует рис. 1.5.

Для упрощения показаны только три канала, на которые поступают сигналы с ₁(t), с ₂(t) и с ₃(t). После прохождения через фильтры нижних частот (ФНЧ) и усилители низкой частоты (УНЧ) эти сигналы преобразуются в сигналы с ₁(t), с ₂(t) и с ₃(t), удовлетворяющие требованиям теоремы Найквиста-Котельникова (рис. 1.4). На амплитудно-импульсные модуляторы (КАИМ) каждого канала от распределителя канальных импульсов (РКИ) поступают периодические последовательности импульсов f ₀₁(t), f ₀₂(t), f ₀₃(t), частоты дискретизации f _д (рис. 1.6).

Периодические последовательности импульсов, управляющие работой канальных амплитудно-импульсных модуляторов и канальных селекторов, формируются генераторным оборудованием передачи ГО_пер и приема. В состав ГО входах задающий генератор ЗГ, формирующий периодическую последовательность импульсов (рис. 1.6); распределитель канальных импульсов (РКИ), который формирует периодические последовательности импульсов f ₀(t) 1-го, 2-го и т.д. до N-го каналов, смещенные относительно друг друга на защитный интервал, необходимые для управления канальными амплитудно-импульсными модуляторами и канальными селекторами (см.рис. 1.5).

На выходе КАИМ каждого из каналов (см. рис. 1.4) формируются АИМ-1 сигналы, которые преобразуются в АИМ-2 сигналы и объединяются в групповой (многоканальный) АИМ сигнал C _Σ(t), который передается по групповому АИМ тракту. С целью обеспечения синхронной работы канальных амплитудно-импульсных модуляторов и селекторов в групповой тракт передачи вводятся синхроимпульсы СИ. Формирование СИ, т.е. придания ему соответствующих признаков (амплитуда, длительность), осуществляется передатчиком синхросигнала Пер.СС. На стороне приема выделение синхросигнала из группового АИМ сигнала осуществляется приемником синхросигнала Пр.СС. Сигнал с выхода Пр.СС синхронизирует генераторное оборудование приема Г0пр. с генераторным оборудованием передачи ГО_пер.

Полоса частот, необходимая для передачи группового АИМ сигнала, может быть определена на основе следующих рассуждений: период дискретизации равен Т_д = 1/ f _д = N *τ_и; для передачи импульса длительностью τ_и достаточна полоса частот Δ f _и =1/τ_и. После соответствующих преобразований формул для Т _д и Δ f _и получим

Δ f _и = N * f _д,

т е. необходима полоса частот от 0 до f _гв = Δ f _и,

где f _гв - верхняя граничная частота полосы пропускания группового АИМ тракта.

С учетом защитного интервала, естественно, полоса частот для передачи группового АИМ сигнала несколько выше. Переходные процессы в групповом АИМ тракте, обусловленные конечной шириной его полосы пропускания, приводят к взаимным влияниям между каналами.

Дата добавления: 2015-08-26