Дискретизация сигналов.

В силу инвариантности преобразования Фурье относительно своего аргумента, т.е. возможности замены в выражениях w на t и наоборот, спектру идеального низкочастотного сигнала должен соответствовать сигнал (во времени) типа 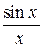, т.е.:

,

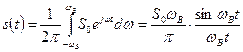где - весовой коэффициент.

Отметим, что нули такого сигнала будут находиться в точках, кратных значению 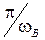.Рассмотрим два ИНЧ сигнала u(t) и v(t), имеющих одинаковую ширину спектра Dw=2w_В, одинаковое значение спектральной плотности S₀, но сдвинутых во времени относительно друг друга на некоторый временной интервал t (рис. 6.2). Спектральная плотность сдвинутого во времени сигнала может быть найдена: 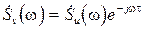, где – спектральные плотности сигналов u(t) и v(t) соответственно. Скалярное произведение этих сигналов

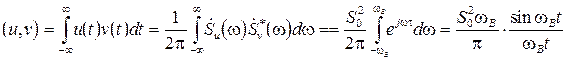(6.1)

Рисунок 6.1 - Сигналы с ограниченным спектром

Рисунок 6.2 - Разнесенные во времени ИНЧ сигналы

Правомочность нахождения скалярного произведения в частотной области будет обоснована в следующем разделе.

Из (6.1) следует, что сигналы u(t) и v(t) будут ортогональны (их скалярное произведение будет равно нулю), если временной сдвиг между ними будет удовлетворять условию . Минимально возможный сдвиг, приводящий к ортогональности, называется интервалом Котельникова t₀ и может быть найден:

, (6.2)

где F_В - верхняя частота (в Гц) в спектре сигнала.

Следовательно, система отсчетных функций типа , сдвинутых друг относительно друга на временные интервалы, кратные t₀, может быть использована для аппроксимации сигналов со спектром, не превышающим значения w_В.

При таком выборе временного сдвига между отсчетными функциями последние обладают тем важным свойством, что в момент времени, когда одна отсчетная функция достигает своего абсолютного максимума, все другие проходят через ноль. Эти узловые точки отстоят друг от друга на интервалы, кратные t₀. (На рис. 6.2 эти точки выделены).

Итак, непрерывный во времени сигнал s(t) со спектром, ограниченным значением w_В, можно разложить в обобщенный ряд Фурье по системе ортогональных функций типа 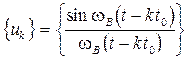, представляющих из себя множество отсчетных функций, сдвинутых друг относительно друга на интервалы времени, кратные .

Билет №13

Дата добавления: 2015-08-27