Метод спектрального исследования линейных цепей

Суть спектрального метода анализа линейных систем заключается в следующем:

(5.33)

- по известному аналитическому выражению для формы входного сигнала находят его спектр:

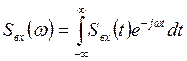
- спектр выходного сигнала находят перемножением и комплексного коэффициента передачи системы :

- по известному спектру выходного сигнала 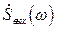находят его форму с помощью обратного преобразования Фурье:

Но из (5.30) следует, что форма сигнала на выходе системы может быть найдена как свертка входного сигнала с характеристикой системы во временной области h(t):

(5.34)

Выражение (5.34) называется интегралом Дюамеля, а h(t) - импульсной переходной характеристикой системы (ИПХ).

Импульсной переходной характеристикой называется реакция (отклик) системы на единичное воздействие в виде дельта - импульса.

Дельта - импульс имеет равномерную спектральную плотность во всем частотном диапазоне S₀=const, поэтому при его воздействии на какую-либо систему спектр выходного сигнала будет с точностью до постоянного коэффициента совпадать с комплексным коэффициентом передачи системы:

Следовательно, реакция системы на дельта - импульс (т.е. ИПХ) может быть найдена с помощью обратного преобразования Фурье:

(5.35)

Для того, чтобы найти значение выходного сигнала системы в какой-либо конкретный момент времени s_вых(t_i), нужно учесть отклики системы на все предшествующие значения входного сигнала:

(5.36)

Рисунок 5.14 - Нахождение формы выходного сигнала методом интеграла Дюамеля

Билет №8

Дата добавления: 2015-08-27