Читайте также:
|
В связи с развитием дискретных логических устройств микроэлектроники, появилась потребность в аппроксимации разрывных сигналов, принимающих два фиксированных значения (скажем ±1) и определенных на некотором, наперед заданном, интервале времени Т. Для этих целей удобно применение ортонормированной системы функций Уолша. Эти функции характерны тем, что на интервале своего существования (–Т/2;Т/2) они принимают значения “+1” или “–1”, которые отличаются лишь знаком.
Введем безразмерное время x=t/t и будем обозначать “ k ”-ую функцию Уолша символом wal (k,x).
Номер функции “ k ” равен числу перемен знака соответствующей функции на интервале ее существования.
По определению при k =0,wal(0,x)=+1, а все остальные функции Уолша могут быть получены произведением соответствующих функций Радэмахера:
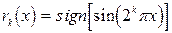(5.56)
Запись sign (сигнум-сигнал) означает функцию знака (рис. 5.18), т.е.
.
Умножение произвольной функции f(t) на sign(t) означает изменение знака функции f(t) в момент времени t=0.
На рис. 5.27 приведены графики первых четырех функций Уолша, полученных по следующему алгоритму:
Любые две функции Уолша ортогональны:
(5.57)
Рисунок 5.27 - Графики функций Уолша
Билет №11
Дата добавления: 2015-08-27; просмотров: 105 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Модуляция сигналов | | | Коды, обнаруживающие ошибки. |