Равномерное квантование

Процесс квантования осуществляется квантующим устройством КУ, амплитудная характеристика которого приведена на рис. 1.12.

Амплитудная характеристика КУ 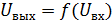представляет собой ступенчатую кривую (рис. 1.12, а). Она может быть представлена в виде суммы идеальной линейной АХ и характеристики, представляющей искажения квантования или шумы квантования (рис. 1.12, б). Характеристика 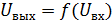имеет две характерных части: участок квантования для 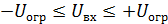и участок ограничения для Соответственно различают шумы квантования, которые представляют случайный процесс с мгновенными значениями ε = | U _вх - U_i | ≤δ/2, и шумы ограничения.

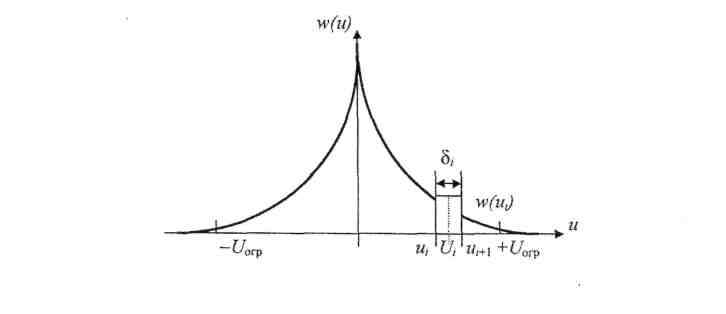
Пусть плотность вероятности распределения мгновенных значений АИМ-2 сигнала описывается функцией w (u) (рис. 1.13) и квантование сигнала, как отмечено выше, осуществляется в пределах от - U _огр до + U _огр для двухполярных сигналов или от 0 до U _огр для однополярных сигналов.

Рис. 1.12. Равномерное квантование

Определим среднюю мощность шума квантования на единичном сопротивлении. Обозначим через u_i и u _i+1 пороги квантования, т.е. границы i -го шага квантования, внутри которого располагается уровень квантования Ui. Ширина i -го шага квантования равна расстоянию между соответствующими порогами

δ_i= u _i+1 - u_i

Рис. 1.13. Плотность распределения мгновенных значений квантуемого сигнала

Если число шагов квантования М достаточно велико, т.е. шаг квантования много меньше среднеквадратического значения квантующего сигнала, то плотность Wi(u) мгновенных значений сигнала внутри i-го шага квантования без особой ошибки можно считать равномерной, т.е. заменить непрерывную кривую w(u) на рис. 1.13 ступенчатой с числом ступеней, равным числу шагов квантования М. Плотность w(u) является условной (условие состоит в попадании сигнала в i -й шаг квантования) и равна

Многочисленные теоретические и экспериментальные исследования показывают, что шумы квантования представляют стационарный и случайный эргодический процесс, статистические характеристики которого, полученные путем усреднения по множеству, совпадают с аналогичными характеристиками, полученными усреднением по времени. Тогда условная средняя мощность шума квантования при условии, что сигнал попадает в i-й шаг квантования (рис. 1.13), равна

(1.26)

Определим значение U_i обеспечивающее минимум Р_кв. Для этого найдем производную Р_кв по Ui и приравняем ее нулю:

Или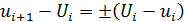

Практический смысл имеет только одно из двух решений

(1.27)

Легко показать, что это значение Ui соответствует минимальной мощности шума квантования (1.26). Следовательно, выгодно располагать уровень квантования посредине между границами соответствующего шага. При этом –δi/2≤ε≤+δi/2, т.е. максимальная ошибка не превышает половины шага квантования, а согласно (1.26) P _квi = δ_i ² /12. Усредним теперь этот результат по всем шагам квантования. Вероятность того, что сигнал попадает в i -й шаг, обозначим через р_i, тогда полная средняя мощность шумов квантования при числе уровней квантования М равна

(1.28)

При равномерном квантовании, т.е. когда и согласно

(1.28)

(1.29)

так как ,из последнего выражения следует, что при равномерном квантовании мощность шума не зависит от закона распределения квантуемого сигнала, а определяется только величиной шага квантования δ.

Находят применение два типа амплитудных характеристик КУ при равномерном симметричном квантовании (рис. 1.12).

При амплитудных характеристиках КУ первого типа (рис. 1.14, а) число уровней (шагов) квантования М четное, число интервалов - нечетное, ни один из уровней не равен нулю.

Для амплитудных характеристик КУ второго типа характерно нечетное число уровней (шагов) квантования и четное число интервалов, один из уровней равен нулю. Для амплитудной характеристики первого типа характерно появление на выходе КУ шумов с амплитудой δ/2 и мощностью δ²/4 при появлении на его входе малейших шумов, так называемых шумов незанятого канала или режим молчания. Максимальная мощность шумов незанятого канала Р_нк = δ²/4 и, следовательно, в 3 раза превышает мощность шума квантования. Для характеристики второго типа незначительные флуктуации на входе КУ не приводят к появлению на выходе каких-либо шумов.

Поскольку Ркв не зависит от величины входного сигнала, то отношение Рс / Ркв растет с увеличением мощности квантуемого сигнала, а следовательно растет и защищенность от шумов квантования Акв. Однако при превышении квантуемым сигналом порога ограничения возникают искажения (шумы) ограничения, и защищенность от суммарного влияния шумов квантования и ограничения снижается.

Групповой АИМ сигнал представляет собой сигналы, поступающие от разных абонентов. Из-за различия их микрофонов, разной длины и типа абонентских линий, их состояния и других факторов эти сигналы могут значительно различаться по мощности. Поскольку параметры последующих узлов цифровых систем передачи при обработке всех сигналов остаются неизменными, то шаг квантования следует выбирать, исходя из того, чтобы шумы квантования не превышали допустимой величины при минимальном сигнале. В то же время во избежание значительных шумов ограничения порог ограничения должен выбираться исходя из параметров максимального по уровню входного сигнала.

Выберем порог ограничения в k раз большим, чем среднеквадратическое значение напряжения ас макс максимального по напряжению сигнала, т.е.

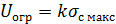(1.30)

Если шкала квантования строится таким образом, чтобы шумы ограничения не возникали, то величина U _огр должна совпадать с пиковым максимальным Uмакс напряжением сигнала. В этом случае коэффициент k показывает, во сколько раз пиковое значение сигнала больше его среднеквадратического значения, и численно совпадает с пикфактором сигнала. Между U _oгp, величиной шага квантования δ и числом уровней квантования М может быть установлена следующая связь: при квантовании двухполярных отсчетов

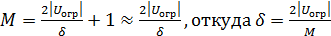(1.31)

при квантовании однополярных отсчетов

(1.32)

Подставив значения U _огр и δ из (1.30)...(1.32) в (1.29), получим для двухполярных сигналов (отсчетов)

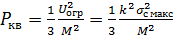(1.33)

для однополярных отсчетов

(1.34)

Мощность сигнала, как случайного процесса, равна его дисперсии

(1.35)

поэтому σ_{с макс} представляет собой мощность наибольшего входного сигнала

Используя (1.33) - (1.35), находим отношение сигнал/шум квантования (ОСШК) и защищенность от шумов квантования для двухполярных сигналов

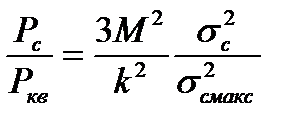
и

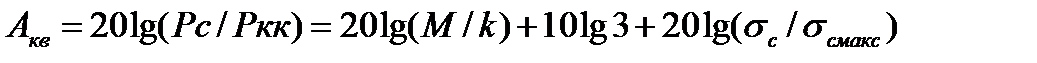
для однополярных сигналов

и

При двоичном m -разрядном кодировании число шагов квантования равно М = 2^m Подставив это значение в (1.36) и (1.37), получим защищенность для двухполярного сигнала

(1.38)

и для однополярных отсчетов

(1.39)

Введем обозначение р_с = 201g(σ_c/σ_cмакс), под которым будем понимать относительный уровень входного квантуемого сигнала. Из последнего уравнения следует

Тогда полученные выражения приводятся к виду для двухполярного сигнала

(1.40)

и для однополярного сигнала

(1.41)

Значения коэффициента k для различных сигналов приведены в табл. 1.1.

Таблица 1.1

Тип сигнала	Гармонический	Речевой	Многоканальный групповой телефонный	Телевизионный(однополярный)
k	√2			√3

Подставив в формулы (1.40) и (1.41) значения параметра k, получим формулы для оценки шумов квантования для различных сигналов.

Формулы (1.40) и (1.41) показывают, что защищенность будет минимальной для слабых сигналов и растет с увеличением их уровня р_с. При дальнейшем увеличении уровня входного сигнала возрастает вероятность появления шумов ограничения и снижение защищенности от суммарного влияния шумов квантования и ограничения.

Защищенность от шумов квантования как функция от уровня сигнала р_с при фиксированном т (или М) и разных k представляет собой семейство параллельных прямых, что будет показано ниже.

Оценку шумов ограничения произведем для сигналов с экспоненциальным распределением мгновенных значений со среднеквадратическим значением а_с, т.е.

(1.42)

Мгновенное значение шума ограничения а его мощность

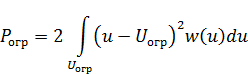
Подставив в эту формулу (1.42) и (1.30), выполнив интегрирование и несложные преобразования, получим мощность шума ограничения

(1.43)

и защищенность от шума ограничения

(1.44)

Защищенность от шумов ограничения как функция р_с представляет собой семейство гипербол, что будет показано ниже.

Из анализа (1.44) следует, что с защищенность растет с увеличением k, что естественно, так как при этом растет порог ограничения U _огр и, следовательно, уменьшается вероятность его превышения. Поскольку шумы квантования и ограничения независимы, мощность суммарного шума, возникающего при квантовании, равна сумме мощностей этих шумов (1.33) и (1.43), т.е.

, (1.45)

суммарная защищенность (

(1.46)

На рис. 1.15 приведены зависимости суммарной защищенности от относительного уровня p_с входного для различных значений k (различных сигналов, см. табл. 1.1) и М= 128 = 2⁷, т.е. т = 7. При построении зависимостей имелось в виду, что для р_с < 0 преобладают шумы квантования, а для р_с > 0 быстро возрастают шумы ограничения. При р_с < 0 преобладают шумы квантования и результирующие характеристики защищенности совпадают с соответствующими прямыми, изображающими зависимости (1.40) и (1.41). При р _с > 0 значительную роль начинают играть шумы ограничения, и характеристика защищенности A_Σ(p_c), постепенно приближаясь, совпадает с одной из гипербол (1.44). Полученные зависимости имеют явно выраженные максимумы, положения которых несколько смещены от точки, где р_с = 0. Следовательно, при равномерном квантовании существует оптимальный уровень входного сигнала р_{с опт}, при квантовании которого защищенность будет наибольшей. Отклонение уровня входного сигнала, как в сторону уменьшения, так и в сторону увеличения приводит к снижению защищенности.

. 1.15. Защищенность от шумов квантования и ограничения как функция входного сигнала

По полученным характеристикам может быть определен диапазон уровней входных сигналов D, в пределах которого защищенность будет выше заданной величины или допустимого значения. Значение D легко может быть определено графически, как показано на рис. 1.15.

Дата добавления: 2015-08-26