Неравномерное квантование

Плотность вероятности w(u) значений телефонного сигнала (рис. 1.13) описывается уравнением (1.42) и характеризуется тем, что малые значения сигнала встречаются гораздо чаще больших. Защищенность от шумов квантования слабых сигналов значительно уступает защищенности сильных сигналов. Так, при диапазоне D = 30 дБ, как следует из рис. 1.15, защищенность слабого сигнала от шумов квантования составляет 20 дБ, а сильных - 40 дБ. Следовательно, при равномерном квантовании создается избыточная защищенность (качество) для сильных сигналов, вероятность появления которых невысока, и недостаточная - для слабых сигналов.

Для удовлетворительной передачи слабых сигналов нужно уменьшать величину шага квантования. Чтобы не увеличивать общее число шагов (уровней) квантования (следовательно, и разрядность двоичного кода при кодировании), можно размер шага сделать переменным, поставив его в зависимость от величины отсчета АИМ-2: квантовать слабые сигналы с малым шагом квантования, а сильные - с большим. При этом защищенность от шумов квантования для слабых сигналов увеличивается, а снижается для сильных, оставаясь, однако, достаточно высокой.

Неравномерное квантование можно реализовать следующими способами:

- путем сжатия (компрессии) динамического диапазона сигнала перед равномерным квантованием и последующего его расширения (экспандирования) после декодирования (рис. 1.16, а); групповой АИМ-2 поступает на компрессор (К), где происходит сжатие его динамического диапазона; квантующее устройство КУ осуществляет равномерное квантование с оптимальным шагом квантования, обеспечивающим допустимую величину защищенности слабых сигналов от шумов квантования; в тракте передачи осуществляются соответствующие преобразования, на его выходе получаем сжатый по динамическому диапазону групповой АИМ сигнал; восстановление исходного динамического диапазона сигнала осуществляется экспандером Э;

- непосредственно в кодирующем устройстве на этапе кодирования отсчетов и обратного преобразования на этапе декодирования {рис..16,6); входной АИМ сигнал поступает на вход нелинейного аналого-цифрового преобразователя НАЦП, где происходят все операции: переход от АИМ-1 к АИМ-2, его неравномерные квантование и кодирование; обратные преобразования происходят в нелинейном цифро-аналоговом преобразователе НЦАП;

- реализация неравномерного квантования при помощи цифрового преобразования после равномерного квантования с мелким шагом (рис. 1.16,в); входной АИМ сигнал поступает на квантующее устройство с малым шагом квантования, обеспечивающим заданную защищенность слабых сигналов от шумов квантования; далее квантованный АИМ сигнал поступает на Кодер, где происходит линейное кодирование кодом с соответствующим числом разрядов; с выхода Кодер сигнал поступает на преобразователь кода передач ПК_пер, где по определенному алгоритму осуществляется преобразование исходного кода в код меньшей разрядности (процесс цифровой компрессии); в преобразователе кода приема ПКпр происходит обратный процесс или цифровое экспандирование; затем сигнал поступает на Декодер, где и происходит восстановление (с ошибкой, конечно) исходного АИМ сигнала.

Первоначально неравномерное или нелинейное квантование было реализовано для отсчетов аналогового сигнала по первому способу. Компрессор и экспандер, вместе взятые, образуют компандер. А процесс компрессии и экспандирования динамического диапазона сигнала называется компандированием. Компандер в ДСП должен реагировать на каждый отсчет сигнала, т.е. быть по возможности безынерционным устройством мгновенного действия.

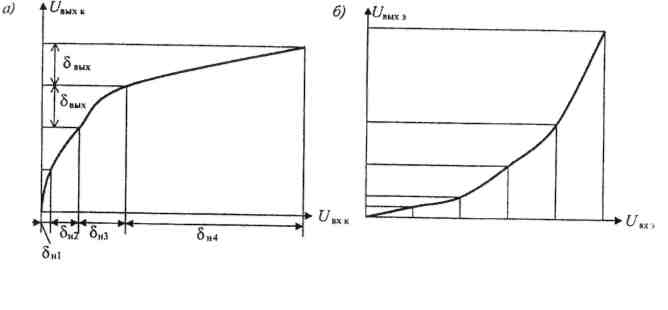
Рис. 1.17. Амплитудные характеристики компрессора и экспандера

Компрессор представляет собой устройство с нелинейной амплитудной характеристикой U _{вых к} = f (U _{вх к}) (рис. 1.17, а), называемой характеристикой компрессии. Квантование выходного сигнала компрессора с равным шагом квантования δ_вых соответствует квантованию входного сигнала с шагом, возрастающим с увеличением уровня входного сигнала

Δ_н1 < δ_н2 < δ_н3

Экспандер представляет собой устройство с нелинейной амплитудной характеристикой (рис. 1.17, б), называемой характеристикой экспандирования.

Как следует из рис. 1.11,а, компрессор обеспечивает большое усиление для слабых сигналов и малое - для сильных, экспандер (рис. 1.17, б) обеспечивает большое усиление для сильных сигналов и малое - для слабых. Амплитудная характеристика экспандера обратна амплитудной характеристике компрессора, т.е.

Экспандер устраняет искажения, вносимые компрессором, так что результирующая амплитудная характеристика компандера, является линейной.

Амплитудная характеристика квантующего устройства с компандером приведена на рис. 1.18. Компрессор включается перед кодером тракта передачи (рис. 1.16, а), а экспандер - на выходе декодера в приемной части.

Защищенность от шумов квантования не зависит от способа реализации характеристики неравномерного квантования. Поэтому вопрос о выборе оптимальной характеристики компрессии можно рассмотреть, не теряя общности, на примере аналогового компандирования. Из рис. 1.17, а следует, что при неравномерном квантовании входного сигнала Uвх шаг квантования равен

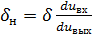(1.47)

Где - производные характеристики компрессии при напряжении входного сигнала σ_с.

Так как мощность шума квантования растет пропорционально квадрату величины шага квантования, а мощность сигнала равна (1.35), то отношение сигнал-шум квантования

(1.48)

будет оставаться постоянным, если шаг квантования будет линейно возрастать с увеличением входного сигнала. Этому соответствует пропорциональная шкала квантования, для которой из (1.47) имеем дифференциальное уравнение

(1.49)

Решением этого дифференциального уравнения является

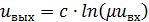(1.49 а)

связывающее напряжение сигнала на входе с напряжением на выходе компрессора с его оптимальной характеристикой, где с и µ - постоянные интегрирования.

Постоянные интегрирования определяются для граничных условий u _вых = 0 при u _вх = 0 и при При этих условиях такая амплитудная характеристика компрессора физически нереализуема, так как при u _вх → 0 u _вых → ∞, а не к нулю. Поэтому практически используются характеристики компрессии, несколько отличающиеся от полученной, но близкой к оптимальной. Эта характеристика описывается уравнением вида:

(1.50)

и называется логарифмической, а µ - параметр, характеризующий степень компрессии (сжатия) динамического диапазона входного сигнала. Ее вид для различных значений µ. приведен на рис. 1.19.

Отношение максимального шага квантования δмакс к минимальному шагу δмин при логарифмическом квантовании равно

(1.51)

Амплитудная характеристика экспандера описывается уравнением вида

(1.52)

Где 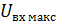- максимальное входное напряжение экспандера.

Иногда пользуются так называемыми нормированными характеристиками µ-закона компандирования, которые получаются заменами в (1.50) вида

`и

-1 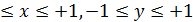(1.52 а)

Мощность шума квантования с неравномерной шкалой с шагом квантования δ_{н i} для двухполярных сигналов на единичном сопротивлении равна (1.28)

С другой стороны, 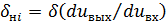(9.47), а - значение шага при равномерном квантовании. При достаточно большом М переходя от суммирования к интегрированию и подставив вместо dUвых/dUвх его значение из (1.50), получим

Для упрощения выводов основных соотношений для оценки шумов квантования и защищенности от них для µ-закона компандирования произведем в последней формуле следующие замены:

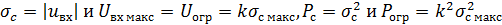
и, выполнив интегрирование. Подставив его в последнюю формулу и выполнив несложные преобразования, получим формулу для оценки защищенности от шумов квантования при неравномерном квантовании

Пусть - относительный уровень напряжения, откуда , подставив это значение в выражение для А_квн

Получим

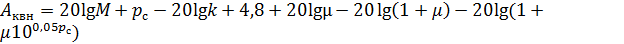(1.53)

При двоичном m-разрядном кодировании число шагов квантования равно М=2^m. Подставив это выражение в (1.53), получим защищенность для двухполярного сигнала при неравномерном квантовании

(1.54)

Сравнение (1.54) с (1.40), показывает, что первые четыре слагаемых представляют собой значение защищенности от шумов квантования при равномерном квантовании А_кв, а три последующих слагаемых

(1.55)

представляют прирост защищенности при неравномерном квантовании, т.е. формулу (1.54) можно записать в таком виде

(1.56)

Для слабых сигналов можно считать, увеличение защищенности для неравномерного квантования по µ-закону командирования равным

(1.57)

Зависимость защищенности от шумов квантования речевого сигнала (k = 5) от относительного уровня сигнала р_с при неравномерном квантовании для m = 8 (или М = 128) и µ= 255, рассчитанная по формуле (1.54), приведена на рис. 1.20. Выбор коэффициента сжатия оказывает влияние на зависимость защищенности от уровня входного сигнала. Это наглядно видно из приведенных на рис. 1.20 характеристик защищенности от относительного уровня входного сигнала при восьмиразрядном кодировании.

Увеличение коэффициента сжатия повышает защищенность для слабых сигналов и ухудшает для сильных. Часто применяют компандирование с коэффициентом сжатия (компрессии) µ= 255. В этом случае защищенность от шумов квантования составляет не менее 25... 30 дБ в динамическом диапазоне входных сигналов более 40 дБ. Соответствующий участок характеристики защищенности отмечен на рис. 1.20 буквами а и. б.

Возможен и другой закон командирования, который получим из следующих рассуждений.

Решение дифференциального уравнения (1.49 а) с учетом обозначений, использованных для получения формулы (1.52а), можно представить в виде Если принять где е основание натуральных логарифмов, то

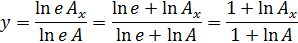
Так как эта функция действует только до определенной точки характеристики х ₁ (рис. 1.21), после которой логарифмическая характеристика переходит в касательную прямую, проходящую через начало координат, то

(1.58)

В этой точке равны производные обеих функций, т.е.

Приравняв последнее выражение к (1.58), получим , что возможно, только если x1=1/ А. Отсюда. Тогда можно записать

(1.59)

Такой закон компандирования называют квазилогарифмическим с линейным касательным отрезком или А-законом компандирования. Здесь А - параметр компрессии, который обычно выбирается равным 87,6. Квантование по А -закону дает примерно такой же выигрыш, как и µ-закон при µ = А, хотя из-за линейности в области слабых сигналов наблюдается некоторое снижение защищенности.

При компандировании по любому закону выигрыш в защищенности для слабых сигналов можно найти по формуле

(1.60)

и для компандирования по А -закону при А = 87,6

Характеристика экспандирования для данного закона определяется как

(1.60 а)

В современных цифровых системах передачи на основе ИКМ-ВРК используют цифровые компандерные устройства, которые объединены и функционируют вместе с кодирующими-декодирующими устройствами, образуя единые функциональные блоки аналого-цифровой преобразователь (АЦП) на передаче и цифро-аналоговый преобразователь (ЦАП) на приеме. При этом в качестве функции компрессии у =f(х) применяют характеристику виртуального компрессора, которая представляет собой аппроксимацию логарифмической характеристики ломаной линией.

Дата добавления: 2015-08-26