
Читайте также:
|
Решим следующую задачу.
Задача. В остроугольном треугольнике ABC проведены высоты AD и BE (рис.5). Доказать, что треугольник DCE подобен треугольнику ABC.
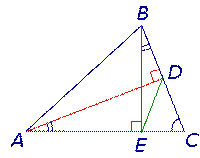
Рис.5
Решение. Рассмотрим треугольники ADC и BEC. Эти треугольники подобны в силу признака подобия прямоугольных треугольников с равными острыми углами (угол C общий). Следовательно, справедливо равенство
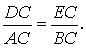
Это равенство, а также наличие общего угла C позволяют на основании признака подобия треугольников заключить, что и треугольники DCE и ABC подобны. Решение задачи завершено.
Из подобия треугольников ABC и EDC (рис.5) вытекает важное следствие.
Следствие 1.
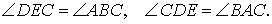
Определение 3. Ортоцентрическим треугольником (ортотреугольником) называют треугольник, вершинами которого служат основания высот исходного треугольника (рис 6).
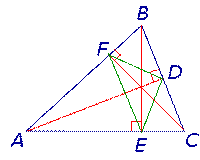
Рис.6
Из определения 3 и следствия 1 вытекает следствие 2.
Следствие 2. Пусть FDE – ортоцентрический треугольник с вершинами в основаниях высот остроугольного треугольника ABC (рис 7).
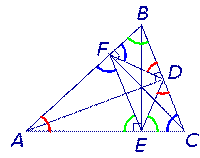
Рис.7
Тогда справедливы равенства
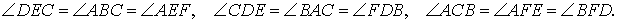
Из следствия 2 вытекает теорема 2.
Теорема 2. Высоты остроугольного треугольника являются биссектрисами углов его ортоцентрического треугольника (рис.7).
Доказательство. Воспользовавшись следствием 2, получаем:
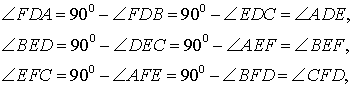
что и требовалось доказать.
***
www.resolventa.ru
Дата добавления: 2015-08-17; просмотров: 132 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Расположение ортоцентров у треугольников различных типов | | | Формы сертификации: обязательная, добровольная, декларация о соответствии. |