Ортоцентр треугольника

Теорема 1. Высоты треугольника (или их продолжения) пересекаются в одной точке.

Доказательство. Рассмотрим произвольный треугольник ABC и проведём через каждую из его вершин прямую, параллельную противолежащей стороне (рис.3).

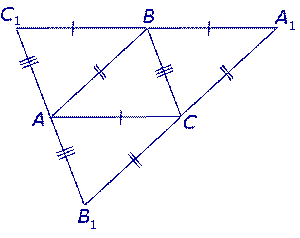
Рис.3

Обозначим точки пересечения этих прямых символами A ₁, B ₁ и C ₁, как показано на рисунке 3.

В силу параллельности прямых AC и C ₁ A ₁, а также BC и C ₁ B ₁ четырёхугольники AC ₁ BC и ABA ₁ C – параллелограммы, откуда вытекают равенства

C ₁ B = AC = BA ₁.

Следовательно, точка B является серединой стороны C ₁ A ₁.

В силу параллельности прямых BC и C ₁ B ₁, а также AB и B ₁ A ₁ четырёхугольники AC ₁ BC и ABCB ₁ – параллелограммы, откуда вытекают равенства

C ₁ A = BC = A ₁ B ₁.

Следовательно, точка A является серединой стороны C ₁ B ₁.

В силу параллельности прямых AB и B ₁ A ₁, а также AC и C ₁ A ₁ четырёхугольники ABA ₁ C и ABCB ₁ – параллелограммы, откуда вытекают равенства

A ₁ C = AB = B ₁ C.

Следовательно, точка C является серединой стороны B ₁ A ₁.

Таким образом, высоты треугольника ABC являются серединными перпендикулярами треугольника A ₁ B ₁ C ₁ (рис. 4),

Рис.4

и в силу теоремы о серединных перпендикулярах пересекаются в одной точке.

Теорема 1 доказана.

Определение 2. Точку пересечения высот треугольника (или их продолжений) называют ортоцентром треугольника.

У треугольников различных типов ортоцентры располагаются по-разному, как показано в следующей таблице.

Дата добавления: 2015-08-17